Cos'è un test alimentare? (spiegazione ed esempio)

Un test di Chow è un test statistico sviluppato dall’economista Gregory Chow che viene utilizzato per verificare se i coefficienti di due diversi modelli di regressione su diversi set di dati sono uguali.

Il test di Chow viene tipicamente utilizzato nel campo dell’econometria con dati di serie temporali per determinare se esiste una rottura strutturale nei dati in un dato momento.

Consideriamo ad esempio il seguente grafico a dispersione:

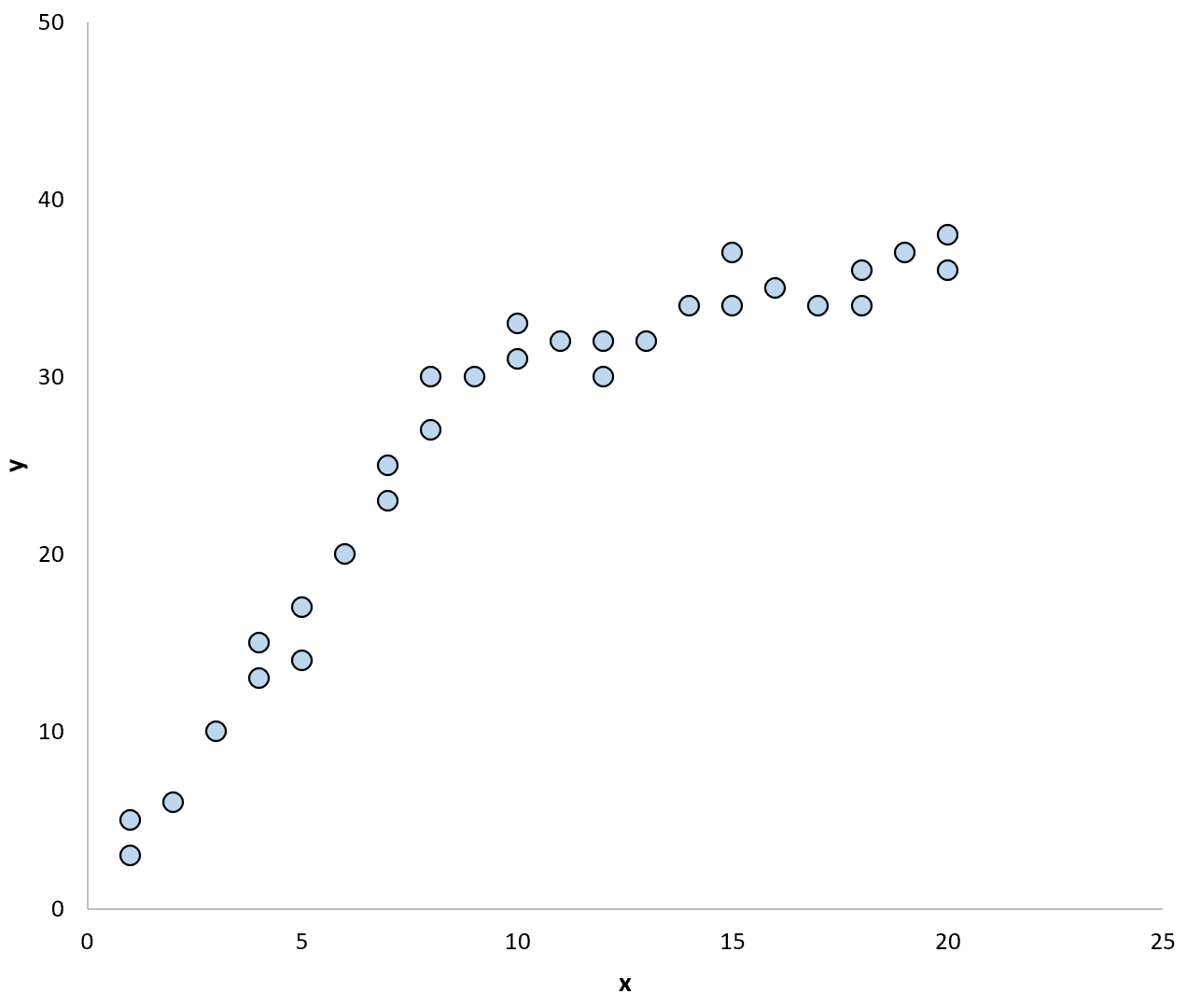
Se utilizzassimo una linea di regressione per riassumere il modello nei dati, potrebbe apparire così:

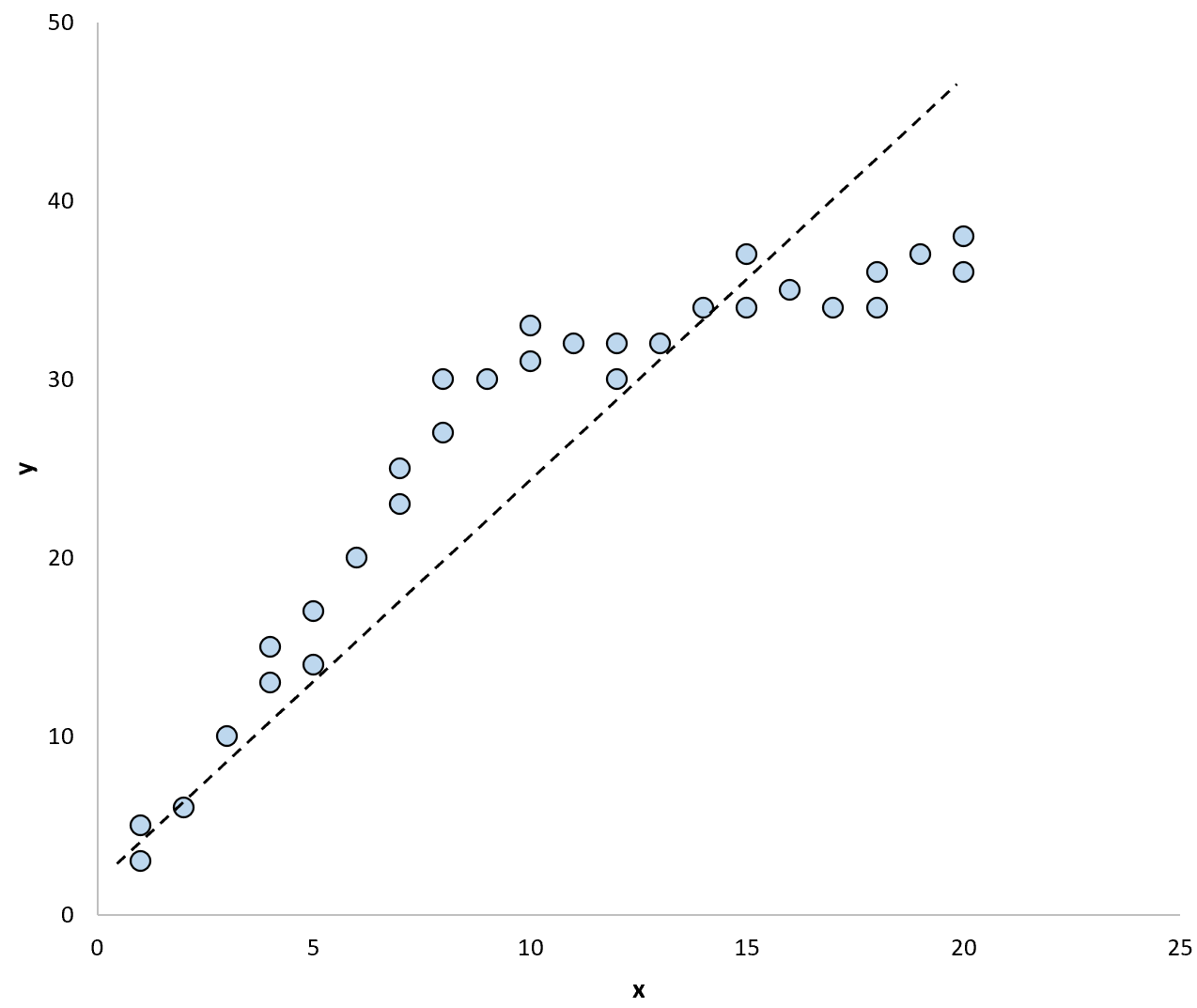
E se utilizzassimo due linee di regressione separate per riassumere il modello nei dati, potrebbe apparire così:

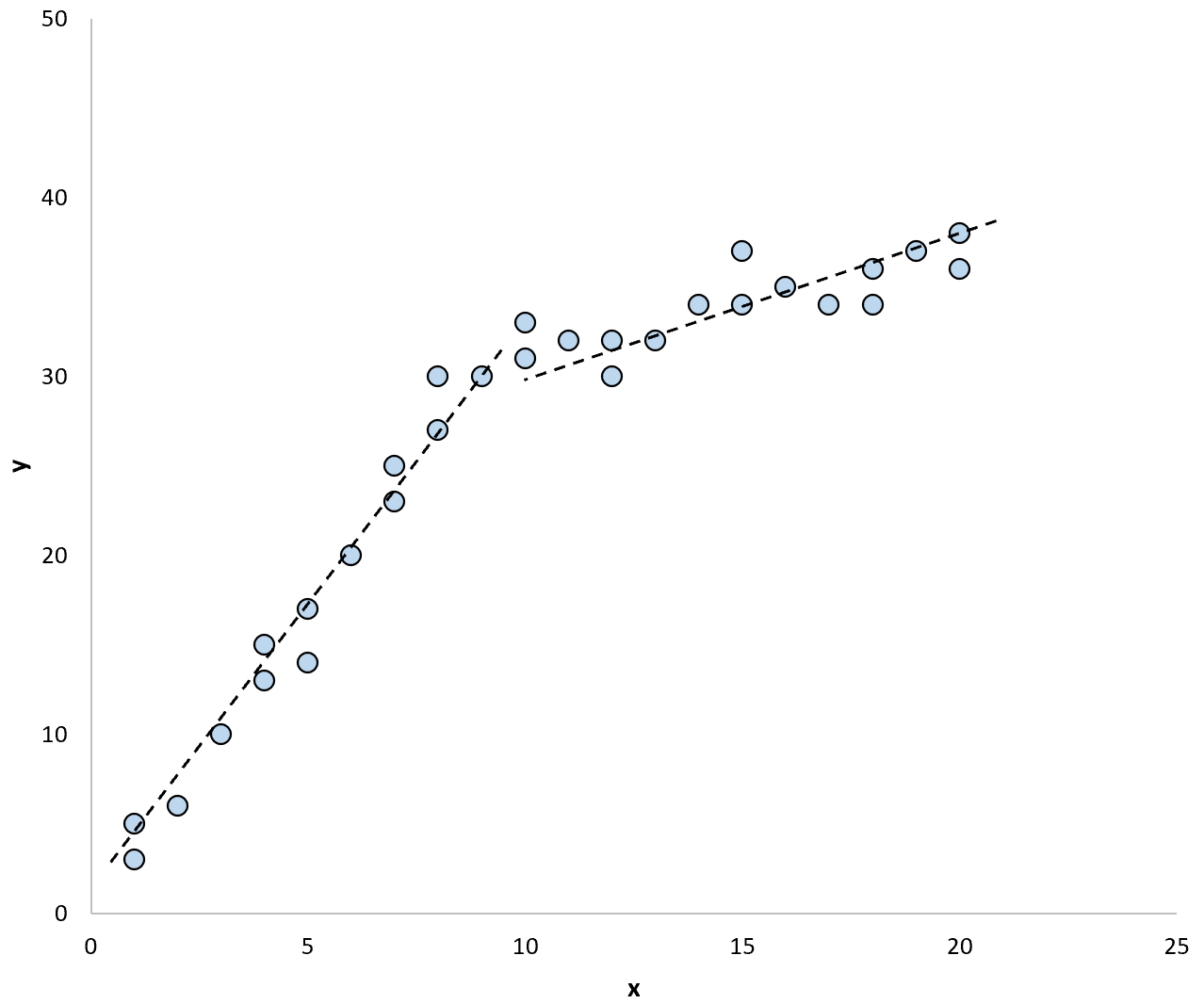
Il test di Chow ci consente di verificare se i coefficienti di regressione di ciascuna retta di regressione sono uguali o meno.

Se il test determina che i coefficienti non sono uguali tra le linee di regressione, ciò significa che esiste una prova significativa di una rottura strutturale nei dati. In altre parole, l’andamento dei dati è molto diverso prima e dopo questo punto di rottura strutturale.

Quando utilizzare il test di Chow

I seguenti esempi illustrano le situazioni in cui potresti voler eseguire un test Chow:

1. Determinare se i prezzi delle azioni si muovono a ritmi diversi prima e dopo le elezioni.

2. Determinare se i prezzi delle case cambiano prima e dopo una variazione del tasso di interesse.

3. Determinare se il profitto medio delle imprese pubbliche è diverso prima e dopo l’adozione di una nuova legge fiscale.

In ogni situazione, potremmo utilizzare un test di Chow per determinare se esiste un punto di rottura strutturale nei dati in un dato momento.

Passaggi per eseguire un test di Chow

Possiamo utilizzare i seguenti passaggi per eseguire un test Chow.

Passaggio 1: Definire le ipotesi nulla e alternativa.

Supponiamo di adattare il seguente modello di regressione al nostro intero set di dati:

• y _t = a + bx _1t + cx _t2 + ε

Supponiamo quindi di dividere i nostri dati in due gruppi in base a un punto di interruzione strutturale e di adattare i seguenti modelli di regressione a ciascun gruppo:

• y _t = a ₁ + b ₁ x _1t + c ₁ x _t2 + ε
• y _t = a ₂ + b ₂ x _1t + c ₂ x _t2 + ε

Utilizzeremmo le seguenti ipotesi nulle e alternative per il test di Chow:

• Nullo (H ₀ ): a ₁ = a ₂ , b ₁ = b ₂ e c ₁ = c ₂
• Alternativa (H _A ): almeno uno dei confronti in Null non è uguale.

Se rifiutiamo l’ipotesi nulla, abbiamo prove sufficienti per affermare che esiste un punto di rottura strutturale nei dati e che due linee di regressione possono adattarsi ai dati meglio di una.

Se non riusciamo a rifiutare l’ipotesi nulla, non abbiamo prove sufficienti per affermare che esiste un punto di rottura strutturale nei dati. In questo caso, diciamo che le linee di regressione possono essere “raggruppate” in un’unica linea di regressione che rappresenta abbastanza bene lo schema dei dati.

Passaggio 2: calcolare la statistica del test.

Se definiamo i seguenti termini:

• S _T : La somma dei quadrati dei residui dei dati totali
• S ₁ , S ₂ : la somma dei quadrati dei residui di ciascun gruppo
• N ₁ , N ₂ : Il numero di osservazioni in ciascun gruppo
• k: il numero di parametri

Possiamo quindi dire che la statistica del test di Chow è:

Statistica del test di Chow = [(S _T – (S ₁ +S ₂ ))/k] / [(S ₁ +S ₂ )/ (N ₁ +N ₂ -2k)]

Questa statistica del test segue la distribuzione F con k e N ₁ +N ₂ -2k gradi di libertà.

Passaggio 3: rifiutare o non rifiutare l’ipotesi nulla.

Se il valore p associato a questa statistica del test è inferiore a un certo livello di significatività , possiamo rifiutare l’ipotesi nulla e concludere che esiste un punto di rottura strutturale nei dati.

Fortunatamente, la maggior parte dei software statistici è in grado di eseguire un test di Chow, quindi probabilmente non dovrai mai eseguire il test manualmente.

Esempio di esecuzione di un test di Chow

Fare riferimento a questo tutorial per vedere un esempio passo passo di come eseguire un test Chow per un determinato set di dati in R.

Note sul test di Chow

Ecco alcune note da tenere a mente riguardo al test Chow:

1. Il test presuppone che i residui dei modelli di regressione siano distribuiti in modo indipendente e identico da una distribuzione normale con varianza sconosciuta.

2. Il test di Chow deve essere utilizzato solo quando la rottura strutturale che si desidera testare si verifica in un momento noto . In altre parole, il test non dovrebbe essere utilizzato ripetutamente per determinare se un dato momento possa essere considerato una rottura strutturale.