Come eseguire un test di chow in r

Un test di Chow viene utilizzato per verificare se i coefficienti di due diversi modelli di regressione su diversi set di dati sono uguali.

Questo test viene generalmente utilizzato nel campo dell’econometria con dati di serie temporali per determinare se esiste una rottura strutturale nei dati in un dato momento.

Questo tutorial fornisce un esempio passo passo di come eseguire un test Chow in R.

Passaggio 1: creare i dati

Per prima cosa creeremo dati falsi:

 #create data
data <- data.frame(x = c(1, 1, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 8, 9, 10, 10,
                         11, 12, 12, 13, 14, 15, 15, 16, 17, 18, 18, 19, 20, 20),
                   y = c(3, 5, 6, 10, 13, 15, 17, 14, 20, 23, 25, 27, 30, 30, 31,
                         33, 32, 32, 30, 32, 34, 34, 37, 35, 34, 36, 34, 37, 38, 36))

#view first six rows of data
head(data)

  xy
1 1 3
2 1 5
3 2 6
4 3 10
5 4 13
6 4 15

Passaggio 2: visualizzare i dati

Successivamente, creeremo un semplice grafico a dispersione per visualizzare i dati:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(data, aes (x = x, y = y)) +
    geom_point(col=' steelblue ', size= 3 )

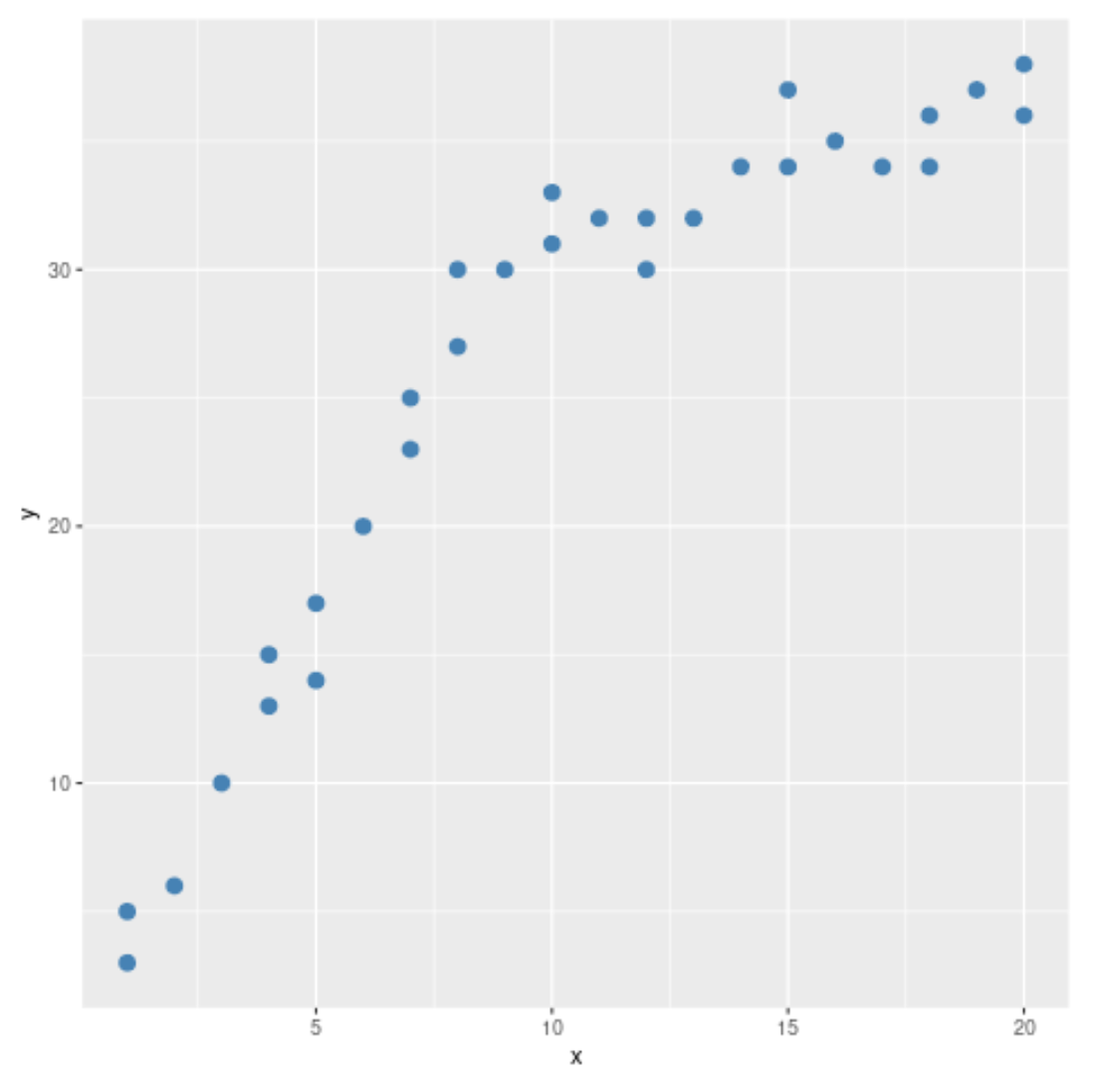
Dal grafico a dispersione, possiamo vedere che lo schema nei dati sembra cambiare in x = 10. Pertanto, possiamo eseguire il test di Chow per determinare se esiste un punto di rottura strutturale nei dati in x = 10.

Passaggio 3: eseguire il test Chow

Possiamo usare la funzione sctest dal pacchetto strucchange per eseguire un test Chow:

 #load strucchange package
library (strucchange)

#perform Chow test
sctest(data$y ~ data$x, type = " Chow ", point = 10 )

	Chow test

data: data$y ~ data$x
F = 110.14, p-value = 2.023e-13

Dal risultato del test possiamo vedere:

• Statistica del test F : 110,14
• valore p: <.0000

Poiché il valore p è inferiore a 0,05, possiamo rifiutare l’ipotesi nulla del test. Ciò significa che abbiamo prove sufficienti per affermare che nei dati è presente un punto di rottura strutturale.

In altre parole, due linee di regressione possono adattare il modello ai dati in modo più efficace rispetto a una singola linea di regressione.