Test u di mann-whitney
Un test U di Mann-Whitney (a volte chiamato test della somma dei ranghi di Wilcoxon) viene utilizzato per confrontare le differenze tra due campioni indipendenti quando le distribuzioni dei campioni non sono distribuite normalmente e le dimensioni del campione sono piccole (n < 30).
È considerato l’equivalente non parametrico del test t indipendente a due campioni .
Ecco alcuni esempi di quando è possibile utilizzare il test U di Mann-Whitney:
- Vuoi confrontare gli stipendi di cinque laureati dell’università A con gli stipendi di cinque laureati dell’università B. Gli stipendi non sono normalmente distribuiti.
- Vuoi sapere se la perdita di peso varia per due gruppi: 12 persone che seguono la dieta A e 10 persone che seguono la dieta B. La perdita di peso non è distribuita normalmente.
- Vuoi sapere se i punteggi di 8 studenti della classe A differiscono da quelli di 7 studenti della classe B. I punteggi non sono distribuiti normalmente.
In ogni esempio, si desidera confrontare due gruppi, le distribuzioni campionarie non sono normali e le dimensioni del campione sono piccole.
Pertanto, un test U di Mann-Whitney è appropriato purché siano soddisfatte le seguenti ipotesi.
Ipotesi del test U di Mann-Whitney
Prima di eseguire un test U di Mann-Whitney, è necessario assicurarsi che siano soddisfatte le seguenti quattro ipotesi:
- Ordinaria o continua: la variabile che stai analizzando è ordinale o continua. Esempi di variabili ordinali includono elementi Likert (ad esempio, una scala a 5 punti che va da “fortemente in disaccordo” a “fortemente d’accordo”). Esempi di variabili continue includono altezza (misurata in pollici), peso (misurata in libbre) o punteggi dei test (misurati da 0 a 100).
- Indipendenza: tutte le osservazioni di entrambi i gruppi sono indipendenti l’una dall’altra.
- Forma: le forme delle distribuzioni per i due gruppi sono approssimativamente le stesse.
Se questi presupposti sono soddisfatti, puoi eseguire un test U di Mann-Whitney.
Come eseguire il test U di Mann-Whitney
Per eseguire un test U di Mann-Whitney, seguiamo la procedura standard di test delle ipotesi in cinque fasi :
1. Indicare le ipotesi.
Nella maggior parte dei casi, il test U di Mann-Whitney viene eseguito come test a due code. Le ipotesi nulla e alternativa si scrivono nella forma:
H 0 : Le due popolazioni sono uguali
H a : Le due popolazioni non sono uguali
2. Determinare un livello di significatività da utilizzare per l’ipotesi.
Decidere il livello di significatività. Le scelte comuni sono .01, .05 e .1.
3. Trova la statistica del test.
La statistica del test è indicata con U ed è il minore tra U 1 e U 2 , come definito di seguito:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
dove n 1 e n 2 sono le dimensioni campionarie rispettivamente per i campioni 1 e 2, e R 1 e R 2 sono la somma dei ranghi rispettivamente per i campioni 1 e 2.
Gli esempi seguenti mostreranno come trovare questa statistica del test in dettaglio.
4. Rifiutare o non rifiutare l’ipotesi nulla.
Utilizzando le statistiche del test, determina se puoi rifiutare o meno l’ipotesi nulla in base al livello di significatività e al valore critico trovati nella tabella U di Mann-Whitney.
5. Interpretare i risultati.
Interpretare i risultati del test nel contesto della domanda posta.
Esempi di esecuzione del test U di Mann-Whitney
Gli esempi seguenti mostrano come eseguire un test U di Mann-Whitney.
Esempio 1
Vogliamo sapere se un nuovo farmaco è efficace o meno nel prevenire gli attacchi di panico. Un totale di 12 pazienti vengono divisi casualmente in due gruppi da 6 e assegnati a ricevere il nuovo farmaco o il placebo. I pazienti registrano quindi il numero di attacchi di panico che hanno sperimentato nel corso di un mese.
I risultati sono mostrati sotto:
| NUOVO FARMACO | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Eseguire un test U di Mann-Whitney per vedere se c’è una differenza nel numero di attacchi di panico tra i pazienti del gruppo placebo rispetto al gruppo del nuovo farmaco. Utilizzare un livello di significatività pari a 0,05.
1. Indicare le ipotesi.
H 0 : Le due popolazioni sono uguali
H a : Le due popolazioni non sono uguali
2. Determinare un livello di significatività da utilizzare per l’ipotesi.
Il problema ci dice che dovremmo utilizzare un livello di significatività pari a 0,05.
3. Trova la statistica del test.
Ricordiamo che la statistica del test è indicata con U ed è la minore tra U 1 e U 2 , come definito di seguito:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
dove n 1 e n 2 sono le dimensioni campionarie rispettivamente per i campioni 1 e 2, e R 1 e R 2 sono la somma dei ranghi rispettivamente per i campioni 1 e 2.
Per trovare R 1 e R 2 , dobbiamo combinare le osservazioni di entrambi i gruppi e ordinarle dal più piccolo al più grande:
| NUOVO FARMACO | PLACEBO |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
Campione totale: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
Gradi: 1.5 , 1.5 , 3 , 4.5 , 4.5 , 6.5 , 6.5 , 8.5 , 8.5 , 10 , 11 , 12
R 1 = somma dei ranghi per il campione 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34
R 2 = somma dei ranghi per il campione 2 = 1,5+3+6,5+10+11+12 = 44
Successivamente, utilizziamo le dimensioni del campione n 1 e n 2 nonché la somma dei ranghi R 1 e R 2 per trovare U 1 e U 2 .
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
Le nostre statistiche di test sono le più piccole tra U1 e U2 , che risulta essere U=13.
Nota: potremmo anche utilizzare il calcolatore del test U di Mann-Whitney per determinare che U = 13.
4. Rifiutare o non rifiutare l’ipotesi nulla.
Utilizzando n 1 = 6 e n 2 = 6 con un livello di significatività di 0,05, la tabella U di Mann-Whitney ci dice che il valore critico è 5:
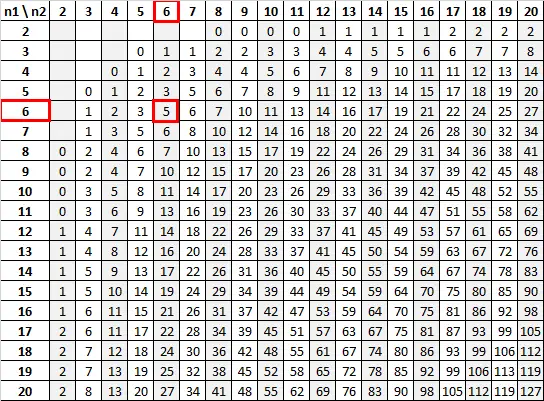
Poiché la nostra statistica test (13) è maggiore del nostro valore critico (5), non riusciamo a rifiutare l’ipotesi nulla.
5. Interpretare i risultati.
Poiché non siamo riusciti a rifiutare l’ipotesi nulla, non abbiamo prove sufficienti per affermare che il numero di attacchi di panico sperimentati dai pazienti nel gruppo placebo è diverso da quello nel gruppo con il nuovo farmaco.
Esempio 2
Vogliamo sapere se studiare 30 minuti al giorno per una settimana aiuta gli studenti a ottenere risultati migliori in un test. Un totale di 15 pazienti vengono assegnati in modo casuale al gruppo di studio o a nessun gruppo di studio. Dopo una settimana, tutti gli studenti sostengono lo stesso test.
I risultati dei test per entrambi i gruppi sono mostrati di seguito:
| STUDIO | NESSUN STUDIO |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Eseguire un test U di Mann-Whitney per vedere se c’è una differenza nei punteggi dei test per il gruppo di studio rispetto al gruppo senza studio. Utilizzare un livello di significatività pari a 0,01.
1. Indicare le ipotesi.
H 0 : Le due popolazioni sono uguali
H a : Le due popolazioni non sono uguali
2. Determinare un livello di significatività da utilizzare per l’ipotesi.
Il problema ci dice che dovremmo utilizzare un livello di significatività pari a 0,01.
3. Trova la statistica del test.
Ricordiamo che la statistica del test è indicata con U ed è la minore tra U 1 e U 2 , come definito di seguito:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
dove n 1 e n 2 sono le dimensioni campionarie rispettivamente per i campioni 1 e 2, e R 1 e R 2 sono la somma dei ranghi rispettivamente per i campioni 1 e 2.
Per trovare R 1 e R 2 , dobbiamo combinare le osservazioni di entrambi i gruppi e ordinarle dal più piccolo al più grande:
| STUDIO | NESSUN STUDIO |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
Campione totale: 72 , 75 , 80 , 81, 84, 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
Righe: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = somma dei ranghi per il campione 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = somma dei ranghi per il campione 2 = 1+2+3+4+6+11+13 = 40
Successivamente, utilizziamo le dimensioni del campione n 1 e n 2 nonché la somma dei ranghi R 1 e R 2 per trovare U 1 e U 2 .
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
Le nostre statistiche di test sono le più piccole tra U1 e U2 , che risulta essere U=12.
Nota: potremmo anche utilizzare il calcolatore del test U di Mann-Whitney per determinare che U = 12.
4. Rifiutare o non rifiutare l’ipotesi nulla.
Utilizzando n 1 = 8 e n 2 = 7 con un livello di significatività di 0,01, la tabella U di Mann-Whitney ci dice che il valore critico è 6:
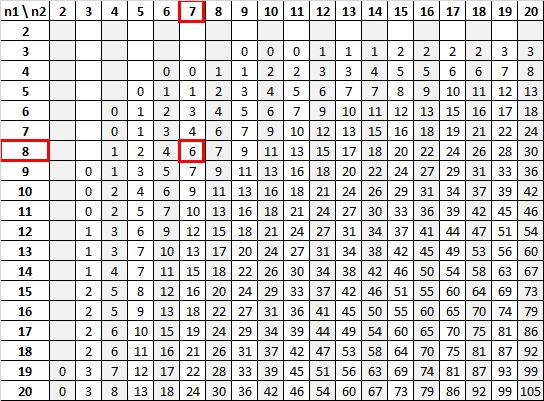
Poiché la nostra statistica test (12) è maggiore del nostro valore critico (6), non riusciamo a rifiutare l’ipotesi nulla.
5. Interpretare i risultati.
Poiché non siamo riusciti a rifiutare l’ipotesi nulla, non abbiamo prove sufficienti per affermare che i punteggi dei test degli studenti che hanno studiato sono diversi da quelli degli studenti che non hanno studiato.
Risorse addizionali
Calcolatrice del test U di Mann-Whitney
Tavolo U di Mann-Whitney
Come eseguire un test U di Mann-Whitney in Excel
Come eseguire un test U di Mann-Whitney in R
Come eseguire un test U di Mann-Whitney in Python
Come eseguire un test U di Mann-Whitney in SPSS
Come eseguire un test U di Mann-Whitney in Stata
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più