Come eseguire il test di tukey in r

Un’ANOVA unidirezionale viene utilizzata per determinare se esiste o meno una differenza statisticamente significativa tra le medie di tre o più gruppi indipendenti.

Se il valore p complessivo della tabella ANOVA è inferiore a un certo livello di significatività, allora abbiamo prove sufficienti per affermare che almeno una delle medie del gruppo è diversa dalle altre.

Tuttavia, questo non ci dice quali gruppi siano diversi gli uni dagli altri. Questo ci dice semplicemente che non tutte le medie dei gruppi sono uguali. Per sapere esattamente quali gruppi sono diversi tra loro, dobbiamo eseguire un test post hoc .

Uno dei test post hoc più comunemente utilizzati è il test di Tukey , che ci consente di eseguire confronti a coppie tra le medie di ciascun gruppo controllando il tasso di errore familiare .

Questo tutorial spiega come eseguire il test di Tukey in R.

Nota: se uno qualsiasi dei gruppi del tuo studio è considerato un gruppo di controllo, dovresti utilizzare invece il test di Dunnett come test post-hoc.

Esempio: test di Tukey in R

Passaggio 1: adattare il modello ANOVA.

Il codice seguente mostra come creare un set di dati falso con tre gruppi (A, B e C) e adattare un modello ANOVA unidirezionale ai dati per determinare se i valori medi di ciascun gruppo sono uguali:

 #make this example reproducible
set.seed(0)

#create data
data <- data.frame(group = rep (c("A", "B", "C"), each = 30),
                   values = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#view first six rows of data
head(data)

  group values
1 A 2.6900916
2 A 0.7965260
3 A 1.1163717
4 A 1.7185601
5 A 2.7246234
6 A 0.6050458

#fit one-way ANOVA model
model <- aov (values~group, data=data)

#view the model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)    
group 2 98.93 49.46 30.83 7.55e-11 ***
Residuals 87 139.57 1.60                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Possiamo vedere che il valore p complessivo dalla tabella ANOVA è 7.55e-11 . Poiché questo numero è inferiore a 0,05, abbiamo prove sufficienti per affermare che i valori medi in ciascun gruppo non sono uguali. Quindi, possiamo eseguire il test di Tukey per determinare esattamente quali medie di gruppo sono diverse.

Passaggio 2: eseguire il test di Tukey.

Il codice seguente mostra come utilizzare la funzione TukeyHSD() per eseguire il test Tukey:

 #perform Tukey's Test
TukeyHSD(model, conf.level= .95 ) 

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = values ~ group, data = data)

$group
         diff lwr upr p adj
BA 0.9777414 0.1979466 1.757536 0.0100545
CA 2.5454024 1.7656076 3.325197 0.0000000
CB 1.5676610 0.7878662 2.347456 0.0000199

Il valore p indica se esiste o meno una differenza statisticamente significativa tra ciascun programma. I risultati mostrano che esiste una differenza statisticamente significativa tra la perdita di peso media di ciascun programma al livello di significatività di 0,05.

Particolarmente:

• Valore P per la differenza delle medie tra B e A: 0,0100545
• Valore P per la differenza delle medie tra C e A: 0,0000000
• Valore P per la differenza delle medie tra C e B: 0,0000199

Passaggio 3: visualizzare i risultati.

Possiamo anche utilizzare la funzione plot(TukeyHSD()) per visualizzare gli intervalli di confidenza:

 #plot confidence intervals
plot(TukeyHSD(model, conf.level= .95 ), las = 2 )

Nota: l’argomento las specifica che le etichette dei segni di spunta devono essere perpendicolari (las=2) all’asse.

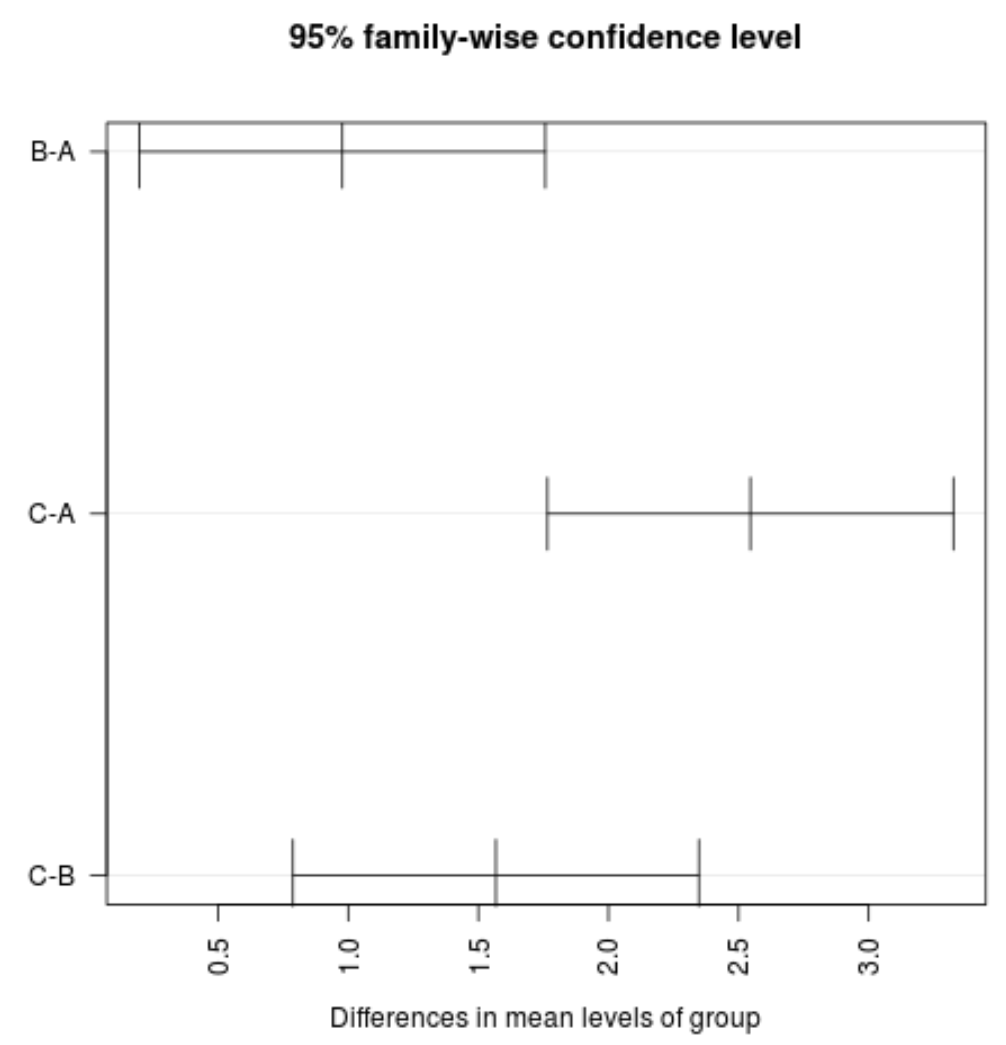
Possiamo vedere che nessuno degli intervalli di confidenza per il valore medio tra i gruppi contiene il valore zero, indicando che esiste una differenza statisticamente significativa nella perdita media tra i tre gruppi. Ciò è coerente con tutti i valori p per i nostri test di ipotesi inferiori a 0,05.

Per questo particolare esempio, possiamo concludere quanto segue:

• I valori medi del gruppo C sono significativamente più alti dei valori medi dei gruppi A e B.
• I valori medi del gruppo B sono significativamente più alti dei valori medi del gruppo A.

Risorse addizionali

Una guida all’utilizzo dei test post-hoc con ANOVA
Come eseguire l’ANOVA unidirezionale in R
Come eseguire l’ANOVA bidirezionale in R