Il test esatto di fisher: definizione, formula ed esempio
Il test esatto di Fisher viene utilizzato per determinare se esiste o meno un’associazione significativa tra due variabili categoriali. Viene generalmente utilizzato come alternativa al test di indipendenza chi quadrato quando uno o più conteggi di celle in una tabella 2 × 2 sono inferiori a 5.
Il test esatto di Fisher utilizza le seguenti ipotesi nulle e alternative:
- H 0 : (ipotesi nulla) Le due variabili sono indipendenti.
- H 1 : (ipotesi alternativa) Le due variabili non sono indipendenti.
Supponiamo di avere la seguente tabella 2×2:
| Gruppo 1 | Gruppo 2 | Totale riga | |
| Categoria 1 | HA | B | a+b |
| Categoria 2 | contro | D | c+d |
| Colonna totale | a+c | b+d | a+b+c+d = n |
Il valore p unilaterale per il test esatto di Fisher viene calcolato come segue:
p = (a+b)!(c+d)!(a+c)!(b+d)! / (a!b!c!d!n!)
Ciò produce lo stesso valore p del CDF della distribuzione ipergeometrica con i seguenti parametri:
- dimensione della popolazione = n
- “successo” della popolazione = a+b
- dimensione del campione = a + c
- esempi di “successo” = uno
Il valore p bilaterale per il test esatto di Fisher è meno semplice da calcolare e non può essere trovato semplicemente moltiplicando il valore p unilaterale per due. Per trovare il valore p a due code, si consiglia di utilizzare il calcolatore del test esatto di Fisher .
Test esatto di Fisher: esempio
Supponiamo di voler sapere se il genere è associato o meno alla preferenza per un partito politico. Prendiamo un semplice campione casuale di 25 elettori e chiediamo loro quale sia la loro preferenza per il partito politico. La tabella seguente presenta i risultati dell’indagine:
| Democratico | Repubblicano | Totale | |
| Maschio | 4 | 9 | 13 |
| Femmina | 8 | 4 | 12 |
| Totale | 12 | 13 | 25 |
Passaggio 1: definire le ipotesi.
Effettueremo il test esatto di Fisher utilizzando le seguenti ipotesi:
- H 0 : Le preferenze di genere e di partito politico sono indipendenti.
- H 1 : Le preferenze di genere e di partito politico non sono indipendenti.
Passaggio 2: calcolo del valore p a due code.
Possiamo utilizzare il calcolatore del test esatto di Fisher con il seguente input:
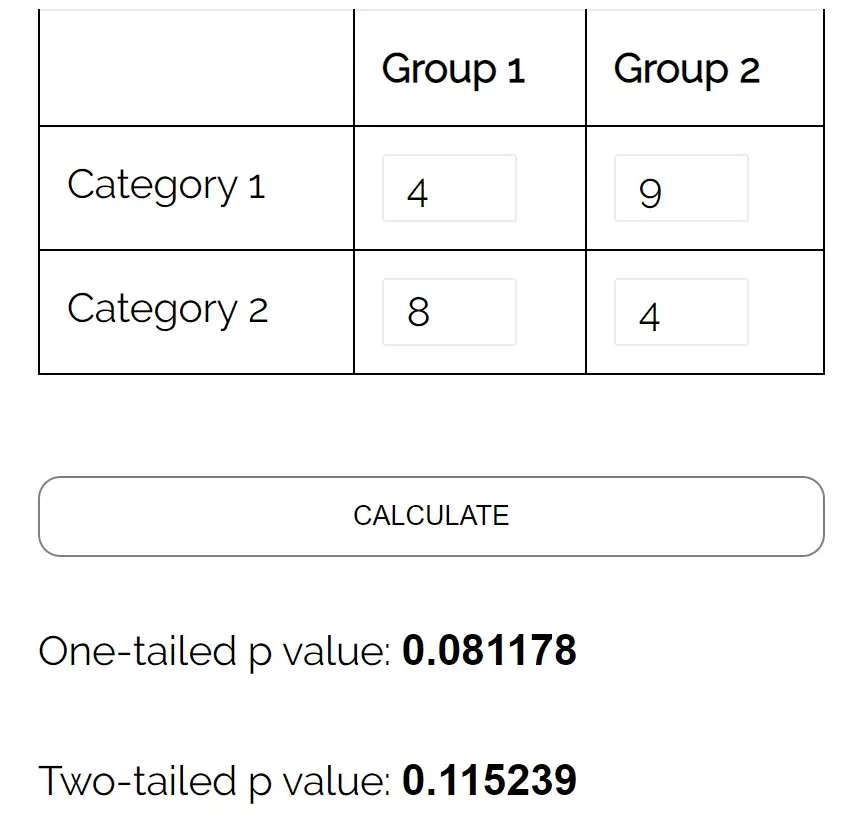
Il valore p a due code è 0,115239 . Essendo questo valore inferiore a 0,05, non possiamo rifiutare l’ipotesi nulla. Non abbiamo prove sufficienti per affermare che esista un’associazione statisticamente significativa tra genere e preferenza per un partito politico.
Risorse addizionali
I seguenti tutorial spiegano come eseguire un test esatto di Fisher utilizzando diversi programmi statistici:
Come eseguire il test esatto di Fisher in R
Come eseguire il test esatto di Fisher in Excel
Come eseguire il test esatto di Fisher in Stata
Come eseguire il test esatto di Fisher in SPSS
Come eseguire il test esatto di Fisher in Python
Calcolatore del test esatto di Fisher