Come eseguire il test di white in sas

Il test di White viene utilizzato per determinare se l’eteroschedasticità è presente in un modello di regressione.

L’eteroschedasticità si riferisce alla dispersione non uniforme dei residui a diversi livelli di una variabile di risposta in un modello di regressione, che viola uno dei presupposti chiave della regressione lineare secondo cui i residui sono equamente dispersi a ciascun livello della variabile di risposta.

Questo tutorial spiega come eseguire il test di White in SAS per determinare se l’eteroschedasticità è o meno un problema in un dato modello di regressione.

Esempio: test del bianco in SAS

Supponiamo di voler adattare un modello di regressione lineare multipla che utilizzi il numero di ore trascorse a studiare e il numero di esami pratici sostenuti per prevedere il voto dell’esame finale degli studenti:

Punteggio esame = β ₀ + β ₁ (ore) + β ₂ (esami preparatori)

Innanzitutto, utilizzeremo il seguente codice per creare un set di dati contenente queste informazioni per 20 studenti:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run ;

/*view dataset*/
proc print data =exam_data; 

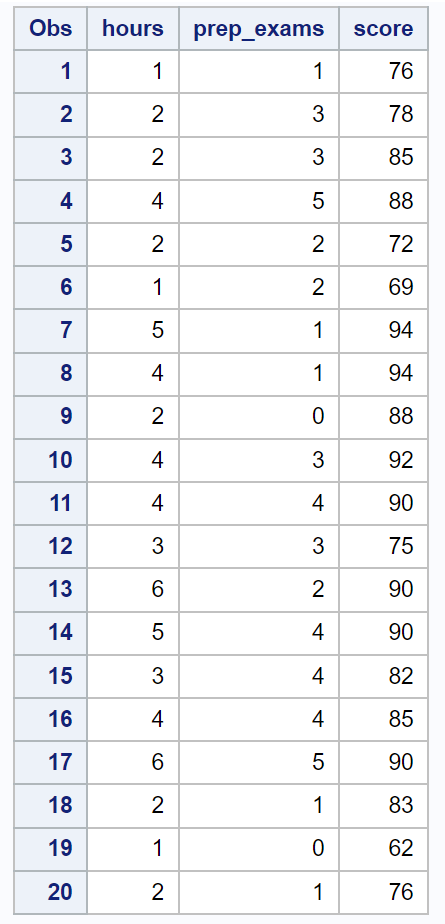
Successivamente, utilizzeremo proc reg per adattare questo modello di regressione lineare multipla nonché l’opzione spec per eseguire il test di White per l’eteroschedasticità:

 /*fit regression model and perform White's test*/
proc reg data =exam_data;
    model score = hours prep_exams / spec ;
run ;
quit ; 

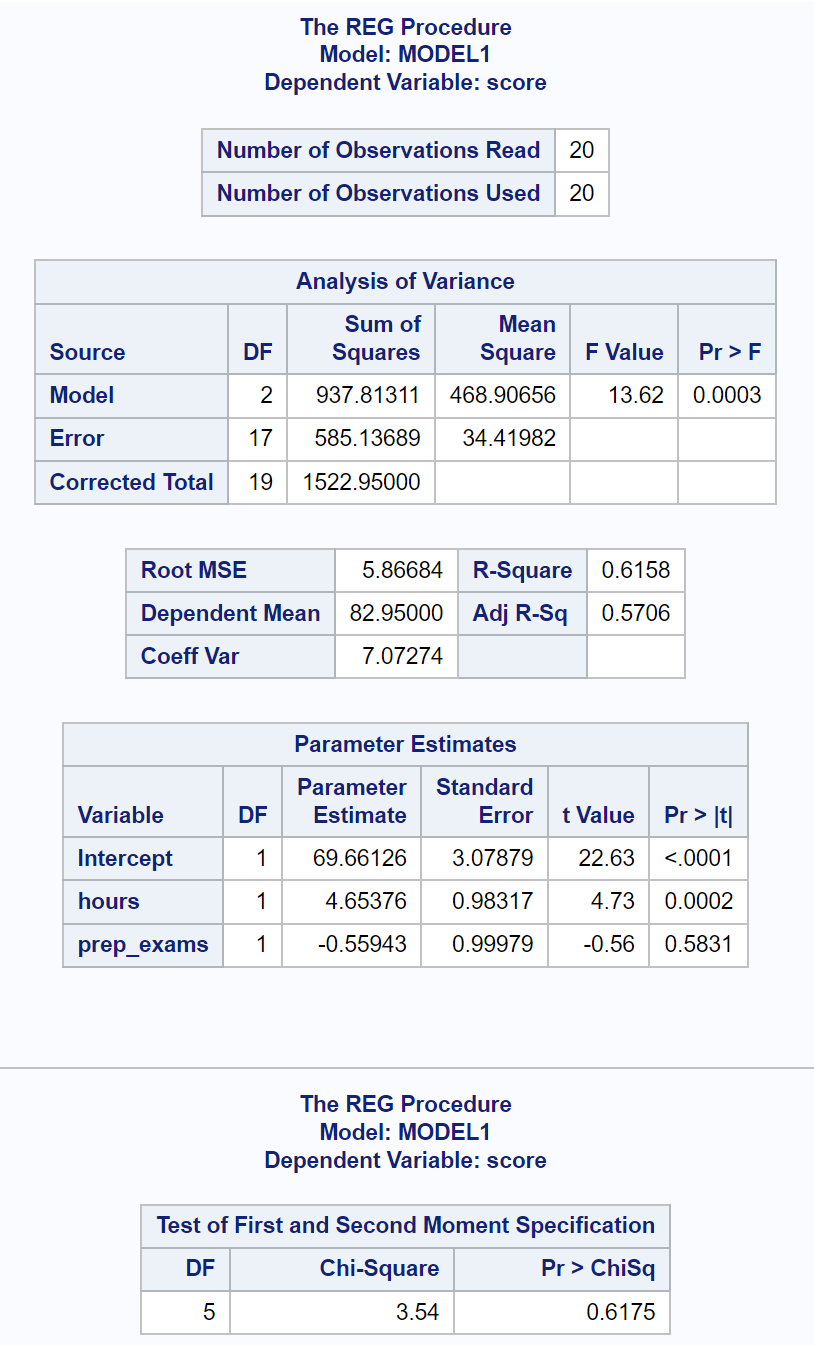
L’ultima tabella dei risultati mostra i risultati del test di White.

Da questa tabella, possiamo vedere che la statistica del test Chi-quadrato è 3,54 e il corrispondente valore p è 0,6175 .

Il test di White utilizza le seguenti ipotesi nulle e alternative:

• Nullo (H ₀ ) : L’eteroschedasticità non è presente.
• Alternativa ( _HA ): è presente eteroschedasticità.

Poiché il valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla.

Ciò significa che non abbiamo prove sufficienti per affermare che l’eteroschedasticità è presente nel modello di regressione.

È quindi possibile interpretare con sicurezza gli errori standard delle stime dei coefficienti nella tabella riepilogativa della regressione.

Cosa fare dopo

Se non si riesce a rifiutare l’ipotesi nulla del test di White, l’eteroschedasticità non è presente e si può procedere a interpretare il risultato della regressione originale.

Tuttavia, se si rifiuta l’ipotesi nulla, significa che nei dati è presente l’eteroschedasticità. In questo caso, gli errori standard visualizzati nella tabella di output della regressione potrebbero essere inaffidabili.

Esistono diversi modi comuni per risolvere questo problema, tra cui:

1. Trasformare la variabile di risposta. Puoi provare a eseguire una trasformazione sulla variabile di risposta.

Ad esempio, puoi utilizzare la variabile di risposta del log invece della variabile di risposta originale.

In generale , prendere il logaritmo della variabile di risposta è un modo efficace per far scomparire l’eteroschedasticità.

Un’altra trasformazione comune consiste nell’utilizzare la radice quadrata della variabile di risposta.

2. Utilizzare la regressione ponderata. Questo tipo di regressione assegna un peso a ciascun punto dati in base alla varianza del relativo valore adattato.

Ciò assegna piccoli pesi ai punti dati che presentano varianze più elevate, riducendo i loro quadrati residui.

Quando vengono utilizzati i pesi appropriati, ciò può eliminare il problema dell’eteroschedasticità.