T-score vs z-score: quando usarli?

Due termini che spesso confondono gli studenti nei corsi di statistica sono t-score e z-score .

Entrambi sono ampiamente utilizzati quando si eseguono test di ipotesi o si costruiscono intervalli di confidenza , ma sono leggermente diversi.

Ecco la formula per ciascuno:

punteggio t = ( x – μ) / (s/√ n )

Oro:

• x : mezzi campione
• μ : media della popolazione
• s : deviazione standard del campione
• n : dimensione del campione

Punteggio z = ( x – μ) / σ

Oro:

• x : valore dei dati grezzi
• μ : media della popolazione
• σ : Deviazione standard della popolazione

Questo diagramma di flusso mostra quando dovresti utilizzarli ciascuno, in base ai tuoi dati:

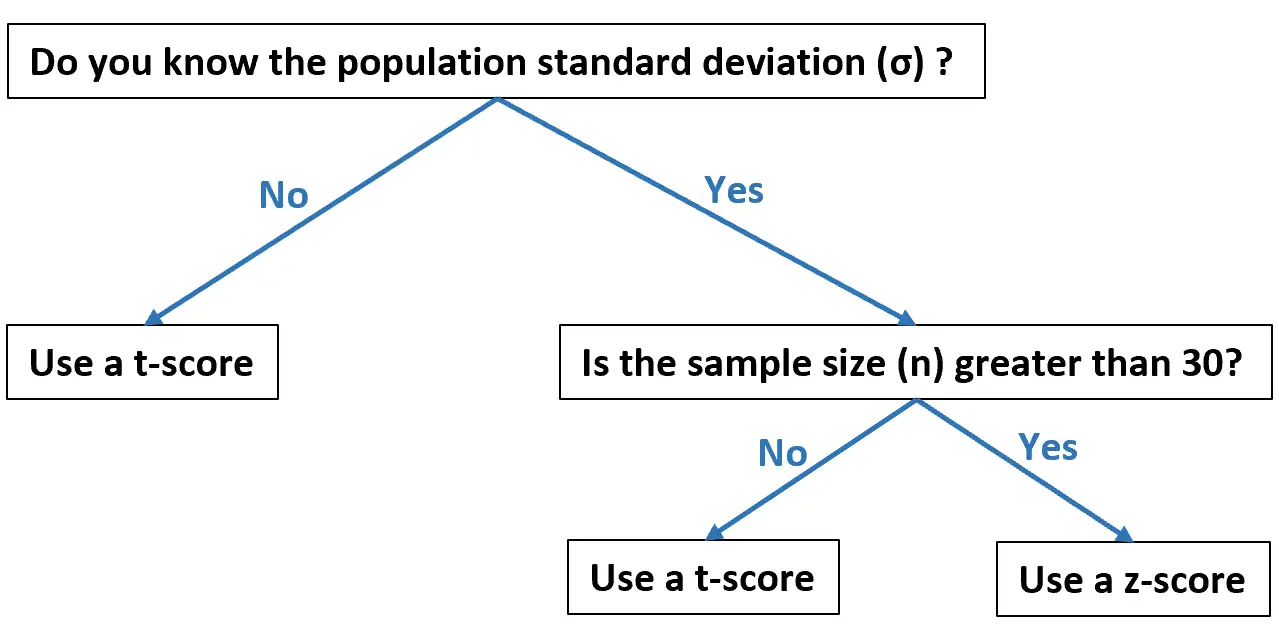
Gli esempi seguenti mostrano come calcolare nella pratica un punteggio T e uno Z-score.

Esempio 1: Calcolo di un T-Score

Supponiamo che un ristorante prepari degli hamburger che dichiarano di avere un peso medio di μ = 0,25 libbre.

Supponiamo di prendere un campione casuale di n = 20 hamburger e di scoprire che il peso medio del campione è x = 0,22 libbre con una deviazione standard di s = 0,05 libbre. Esegui un test di ipotesi per determinare se il peso medio effettivo di tutti gli hamburger prodotti da questo ristorante è pari a 0,25 libbre.

Per questo esempio, utilizzeremmo un punteggio T per eseguire il test di ipotesi perché nessuna delle due condizioni seguenti è soddisfatta.

• La deviazione standard della popolazione (σ) è nota. (σ non è fornito in questo esempio)
• La dimensione del campione è maggiore di 30. (n=20 in questo esempio)

Quindi, calcoleremo il punteggio t come segue:

• punteggio t = ( x – μ) / (s/√ n )
• punteggio t = (0,22 – 0,25) / (0,05 / √ 20 )
• Punteggio t = -2,68

Secondo il calcolatore del punteggio T del valore P , il valore P che corrisponde a questo punteggio T è 0,01481 .

Poiché questo valore p è inferiore a 0,05, abbiamo prove sufficienti per affermare che il peso medio degli hamburger prodotti in questo ristorante non è pari a 0,25 libbre.

Esempio 2: calcolo di un punteggio Z

Supponiamo che un’azienda produca batterie la cui durata di vita è nota per seguire una distribuzione normale con una media di μ = 20 ore e una deviazione standard di σ = 5 ore.

Supponiamo di prendere un campione casuale di n = 50 batterie e di scoprire che la media del campione è x = 21 ore. Eseguire un test di ipotesi per determinare se la vita media reale di tutte le batterie prodotte da questa azienda è pari a 20 ore.

Per questo esempio, utilizzeremmo un punteggio z per eseguire il test di ipotesi perché sono soddisfatte entrambe le seguenti condizioni:

• La deviazione standard della popolazione (σ) è nota. (σ è uguale a 5 in questo esempio)
• La dimensione del campione è maggiore di 30. (n=50 in questo esempio)

Quindi, calcoleremo il punteggio z come segue:

• Punteggio z = ( x – μ) / σ
• Punteggio z = (21 – 20) / 5
• Punteggio z = 0,2

Secondo il calcolatore del punteggio Z del valore P, il valore p che corrisponde a questo punteggio z è 0,84184 .

Poiché questo valore p non è inferiore a 0,05, non abbiamo prove sufficienti per affermare che la durata media di tutte le batterie prodotte da questa azienda sia diversa da 20 ore.

Risorse addizionali

I seguenti tutorial offrono ulteriori informazioni sui punteggi T e Z:

Distribuzione normale vs distribuzione t: qual è la differenza?
Come leggere la tabella di distribuzione t
Come leggere la tabella Z