Come utilizzare la distribuzione esponenziale in python

La distribuzione esponenziale è una distribuzione di probabilità utilizzata per modellare il tempo che dobbiamo aspettare prima che si verifichi un determinato evento.

Se una variabile casuale X segue una distribuzione esponenziale, allora la funzione di distribuzione cumulativa di X può essere scritta:

F (x; λ) = 1 – e ^-λx

Oro:

• λ: il parametro della velocità (calcolato come λ = 1/μ)
• e: Una costante pari a circa 2.718

Questo tutorial spiega come utilizzare la distribuzione esponenziale in Python.

Come generare una distribuzione esponenziale

Puoi utilizzare la funzione expon.rvs(scale, size) dalla libreria SciPy in Python per generare valori casuali da una distribuzione esponenziale con un parametro di velocità e una dimensione del campione specifici:

 from scipy. stats import expo

#generate random values from exponential distribution with rate=40 and sample size=10
expon. rvs (scale= 40 , size= 10 )

array([116.5368323 , 67.23514699, 12.00399043, 40.74580584,
        34.60922432, 2.68266663, 22.70459831, 97.66661811,
         6.64272914, 46.15547298])

Nota : puoi trovare la documentazione completa della libreria SciPy qui .

Come calcolare le probabilità utilizzando una distribuzione esponenziale

Supponiamo che il numero medio di minuti tra le eruzioni di un determinato geyser sia di 40 minuti. Quanto è probabile che dovremo aspettare meno di 50 minuti per un’eruzione?

Per risolvere questo problema, dobbiamo prima calcolare il parametro della velocità:

• λ = 1/μ
• λ = 1/40
• λ = 0,025

Possiamo inserire λ = 0,025 e x = 50 nella formula CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0,025(50)
• P(X ≤ 50) = 0,7135

La probabilità che dovremo aspettare meno di 50 minuti per la prossima eruzione è 0,7135 .

Possiamo usare la funzione expon.cdf() di SciPy per risolvere questo problema in Python:

 from scipy. stats import expo

#calculate probability that x is less than 50 when mean rate is 40
expon. cdf (x=50, scale=40)

0.7134952031398099

La probabilità che dovremo aspettare meno di 50 minuti per la prossima eruzione è 0,7135 .

Ciò corrisponde al valore che abbiamo calcolato manualmente.

Come tracciare una distribuzione esponenziale

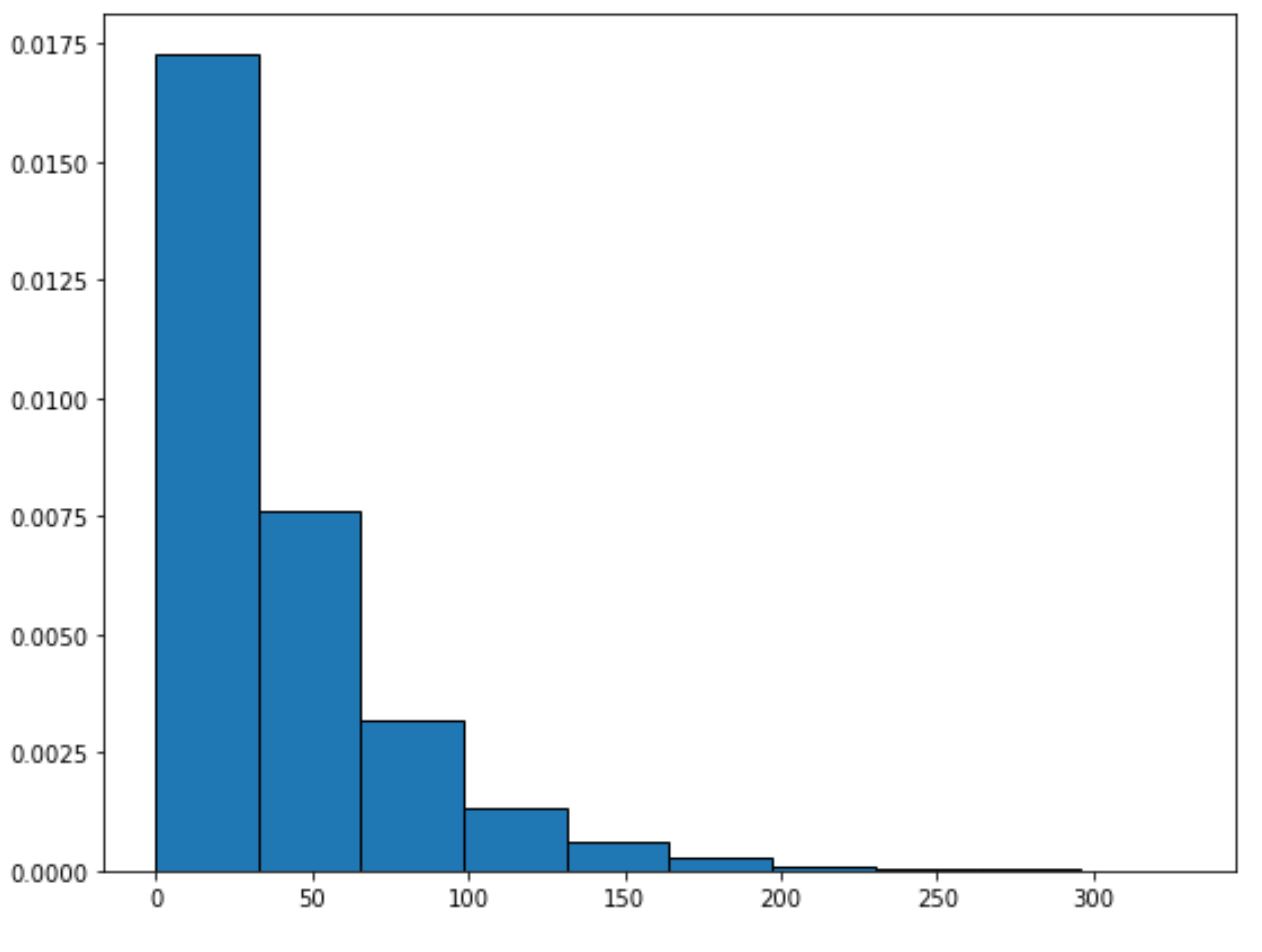
È possibile utilizzare la seguente sintassi per tracciare una distribuzione esponenziale con un determinato parametro di velocità:

 from scipy. stats import expo
import matplotlib. pyplot as plt

#generate exponential distribution with sample size 10000
x = expon. rvs (scale= 40 ,size= 10000 )

#create plot of exponential distribution
plt. hist (x, density= True , edgecolor=' black ')

Risorse addizionali

I seguenti tutorial spiegano come utilizzare altre distribuzioni comuni in Python:

Come utilizzare la distribuzione di Poisson in Python
Come usare la distribuzione t in Python
Come utilizzare la distribuzione uniforme in Python