Come eseguire la regressione logistica in python (passo dopo passo)

La regressione logistica è un metodo che possiamo utilizzare per adattare un modello di regressione quando la variabile di risposta è binaria.

La regressione logistica utilizza un metodo noto come stima di massima verosimiglianza per trovare un’equazione della seguente forma:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Oro:

• X _j : la j- ^esima variabile predittiva
• β _j : stima del coefficiente per la j ^-esima variabile predittiva

La formula sul lato destro dell’equazione prevede le probabilità logaritmiche che la variabile di risposta assuma il valore 1.

Pertanto, quando adattiamo un modello di regressione logistica, possiamo utilizzare la seguente equazione per calcolare la probabilità che una data osservazione assuma il valore 1:

p(X) = ^{eβ ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

Utilizziamo quindi una certa soglia di probabilità per classificare l’osservazione come 1 o 0.

Ad esempio, potremmo dire che le osservazioni con probabilità maggiore o uguale a 0,5 saranno classificate come “1” e tutte le altre osservazioni saranno classificate come “0”.

Questo tutorial fornisce un esempio passo passo di come eseguire la regressione logistica in R.

Passaggio 1: importa i pacchetti necessari

Per prima cosa importeremo i pacchetti necessari per eseguire la regressione logistica in Python:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

Passaggio 2: caricare i dati

Per questo esempio, utilizzeremo il set di dati predefinito dal libro Introduction to Statistical Learning . Possiamo utilizzare il seguente codice per caricare e visualizzare un riepilogo del set di dati:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

Questo set di dati contiene le seguenti informazioni su 10.000 individui:

• default: indica se un individuo è inadempiente o meno.
• studente: indica se un individuo è studente o meno.
• saldo: saldo medio portato da un individuo.
• reddito: reddito dell’individuo.

Utilizzeremo lo status di studente, il saldo bancario e il reddito per costruire un modello di regressione logistica che predice la probabilità che un dato individuo vada in default.

Passaggio 3: creare campioni di formazione e test

Successivamente, divideremo il set di dati in un set di training su cui addestrare il modello e un set di test su cui testare il modello.

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

Passaggio 4: adattare il modello di regressione logistica

Successivamente, utilizzeremo la funzione LogisticRegression() per adattare un modello di regressione logistica al set di dati:

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

Passaggio 5: diagnostica del modello

Una volta adattato il modello di regressione, possiamo analizzare le prestazioni del nostro modello sul set di dati di test.

Per prima cosa creeremo la matrice di confusione per il modello:

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

Dalla matrice di confusione possiamo vedere che:

• #Pronostici veri positivi: 2886
• #Pronostici veri negativi: 0
• #Pronostici falsi positivi: 113
• #Predizioni false negative: 1

Possiamo anche ottenere il modello di accuratezza, che ci dice la percentuale di previsioni di correzione effettuate dal modello:

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

Questo ci dice che il modello ha fatto la previsione corretta riguardo al fatto se un individuo sarebbe andato in default o meno nel 96,2% dei casi.

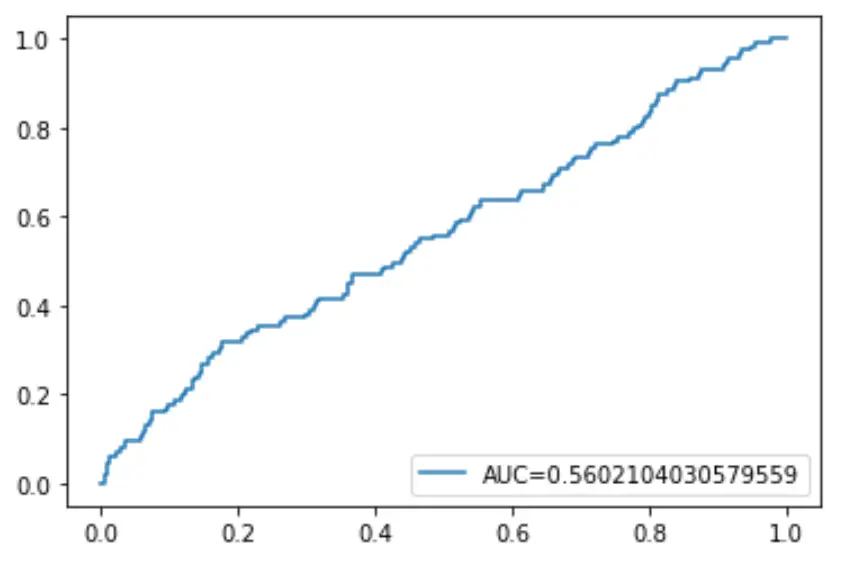
Infine, possiamo tracciare la curva ROC (Receiver Operating Characteristic) che mostra la percentuale di veri positivi previsti dal modello quando la soglia di probabilità di previsione viene abbassata da 1 a 0.

Maggiore è l’AUC (area sotto la curva), più accuratamente il nostro modello è in grado di prevedere i risultati:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()