Come eseguire la regressione ols in python (con esempio)

La regressione dei minimi quadrati ordinari (OLS) è un metodo che ci consente di trovare una linea che meglio descrive la relazione tra una o più variabili predittive e una variabile di risposta .

Questo metodo ci permette di trovare la seguente equazione:

ŷ = b ₀ + b ₁ x

Oro:

• ŷ : il valore di risposta stimato
• b ₀ : L’origine della retta di regressione
• b ₁ : La pendenza della retta di regressione

Questa equazione può aiutarci a comprendere la relazione tra il predittore e la variabile di risposta e può essere utilizzata per prevedere il valore di una variabile di risposta dato il valore della variabile predittore.

Il seguente esempio passo passo mostra come eseguire la regressione OLS in Python.

Passaggio 1: creare i dati

Per questo esempio, creeremo un set di dati contenente le seguenti due variabili per 15 studenti:

• Numero totale di ore studiate
• Risultato dell’esame

Eseguiremo una regressione OLS, utilizzando le ore come variabile predittiva e il punteggio dell’esame come variabile di risposta.

Il codice seguente mostra come creare questo set di dati falso in panda:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

Passaggio 2: eseguire una regressione OLS

Successivamente, possiamo utilizzare le funzioni nel modulo statsmodels per eseguire una regressione OLS, utilizzando le ore come variabile predittrice e il punteggio come variabile di risposta :

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

Dalla colonna coef , possiamo vedere i coefficienti di regressione e scrivere la seguente equazione di regressione adattata:

Punteggio = 65.334 + 1.9824*(ore)

Ciò significa che ogni ora aggiuntiva studiata è associata ad un aumento del punteggio medio dell’esame di 1,9824 punti.

Il valore originale di 65.334 ci dice il punteggio medio previsto per l’esame per uno studente che studia per zero ore.

Possiamo anche utilizzare questa equazione per trovare il punteggio atteso dell’esame in base al numero di ore di studio di uno studente.

Ad esempio, uno studente che studia per 10 ore dovrebbe ottenere un punteggio d’esame di 85.158 :

Punteggio = 65.334 + 1.9824*(10) = 85.158

Ecco come interpretare il resto del riepilogo del modello:

• P(>|t|): Questo è il valore p associato ai coefficienti del modello. Poiché il p-value per le ore (0,000) è inferiore a 0,05, possiamo dire che esiste un’associazione statisticamente significativa tra ore e punteggio .
• R quadrato: questo ci dice che la percentuale di variazione nei punteggi degli esami può essere spiegata dal numero di ore studiate. In questo caso, l’83,1% della variazione dei punteggi è spiegabile con le ore studiate.
• Statistica F e valore p: la statistica F ( 63,91 ) e il corrispondente valore p ( 2,25e-06 ) ci dicono il significato complessivo del modello di regressione, cioè se le variabili predittive nel modello sono utili per spiegare la variazione. nella variabile di risposta. Poiché il valore p in questo esempio è inferiore a 0,05, il nostro modello è statisticamente significativo e le ore sono considerate utili per spiegare la variazione del punteggio .

Passaggio 3: Visualizza la linea più adatta

Infine, possiamo utilizzare il pacchetto di visualizzazione dati matplotlib per visualizzare la linea di regressione adattata ai punti dati effettivi:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

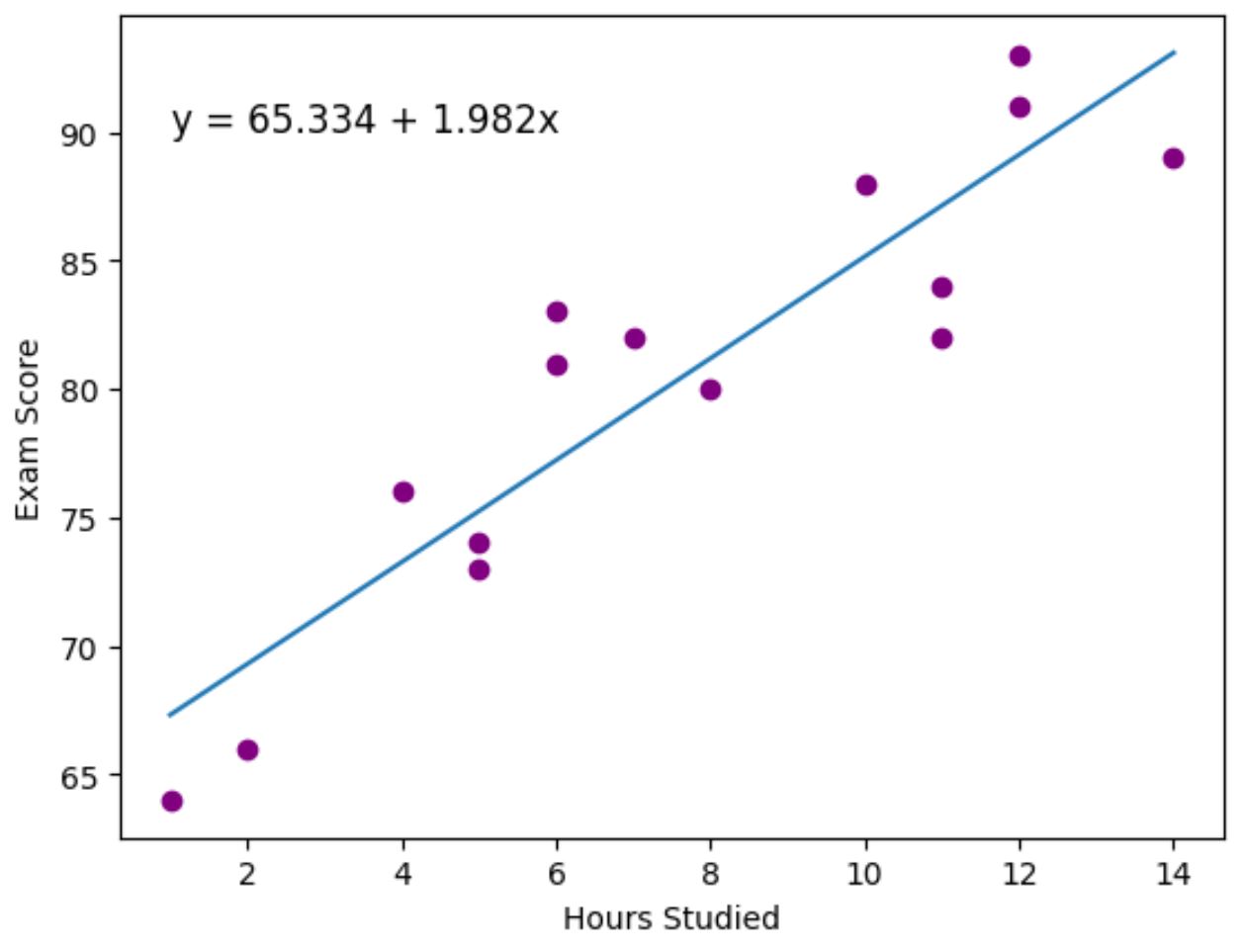
I punti viola rappresentano i punti dati effettivi e la linea blu rappresenta la linea di regressione adattata.

Abbiamo utilizzato anche la funzione plt.text() per aggiungere l’equazione di regressione adattata nell’angolo in alto a sinistra del grafico.

Osservando il grafico, sembra che la linea di regressione adattata catturi abbastanza bene la relazione tra la variabile ore e la variabile punteggio .

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in Python:

Come eseguire la regressione logistica in Python
Come eseguire la regressione esponenziale in Python
Come calcolare l’AIC dei modelli di regressione in Python