Come eseguire la regressione polinomiale in python

L’analisi di regressione viene utilizzata per quantificare la relazione tra una o più variabili esplicative e una variabile di risposta.

Il tipo più comune di analisi di regressione è la regressione lineare semplice , utilizzata quando una variabile predittore e una variabile di risposta hanno una relazione lineare.

Tuttavia, a volte la relazione tra una variabile predittore e una variabile di risposta non è lineare.

Ad esempio, la vera relazione può essere quadratica:

Oppure può essere cubico:

In questi casi, ha senso utilizzare la regressione polinomiale , che può tenere conto della relazione non lineare tra le variabili.

Questo tutorial spiega come eseguire la regressione polinomiale in Python.

Esempio: regressione polinomiale in Python

Supponiamo di avere la seguente variabile predittore (x) e variabile di risposta (y) in Python:

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

Se creiamo un semplice grafico a dispersione di questi dati, possiamo vedere che la relazione tra x e y è chiaramente non lineare:

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

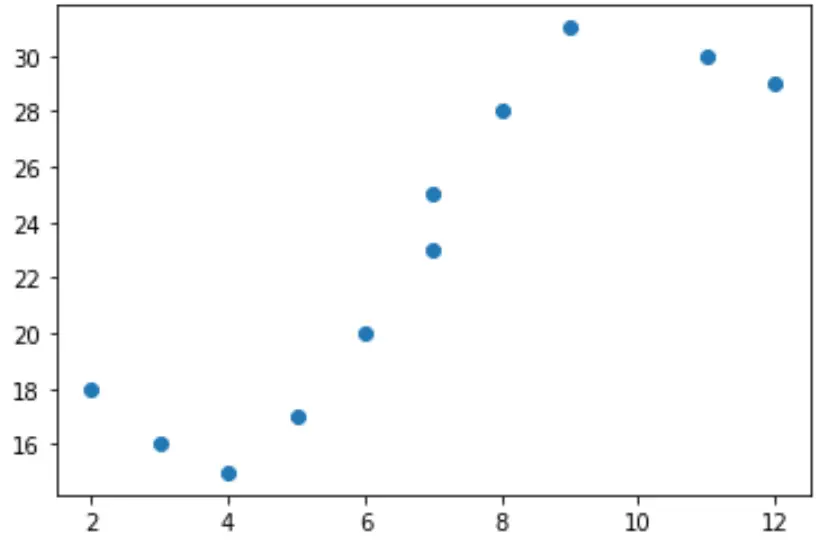
Non avrebbe quindi senso adattare a questi dati un modello di regressione lineare. Invece, possiamo tentare di adattare un modello di regressione polinomiale con grado 3 utilizzando la funzione numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

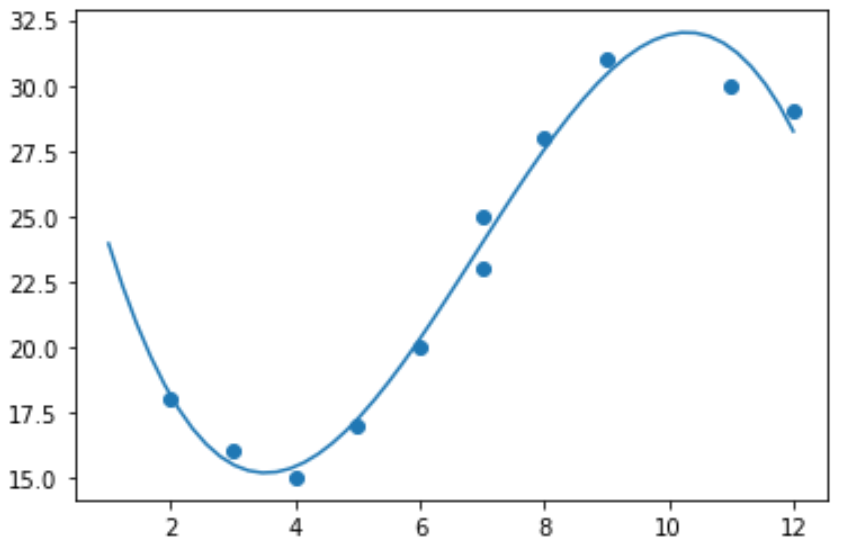
Possiamo ottenere l’equazione di regressione polinomiale adattata stampando i coefficienti del modello:

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

L’equazione di regressione polinomiale adattata è:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Questa equazione può essere utilizzata per trovare il valore atteso della variabile di risposta dato un dato valore della variabile esplicativa.

Ad esempio, supponiamo x = 4. Il valore atteso per la variabile di risposta, y, sarebbe:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39 .

Possiamo anche scrivere una breve funzione per ottenere l’R quadrato del modello, ovvero la proporzione della varianza nella variabile di risposta che può essere spiegata dalle variabili predittive.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

In questo esempio, il quadrato R del modello è 0,9841 .

Ciò significa che il 98,41% della variazione nella variabile di risposta può essere spiegato dalle variabili predittive.