Radice media quadrata

Di Benjamin anderson Agosto 6, 2023 Statistiche 0 commenti

Qui spieghiamo cos’è la radice quadrata media e come viene calcolata. Inoltre, imparerai i vantaggi e gli svantaggi dell’utilizzo della media e un esercizio risolto passo dopo passo. Infine, sarai in grado di calcolare la radice quadrata di qualsiasi set di dati con la calcolatrice alla fine dell’articolo.

Qual è il quadrato medio?

La radice quadrata media è una misura della centralità della statistica descrittiva. La radice quadrata media è uguale alla radice quadrata della media aritmetica dei quadrati dei dati.

La radice quadrata media è anche chiamata radice quadrata media o RMS .

La formula per la media quadratica è quindi la seguente:

La media quadrata è particolarmente utile quando la variabile statistica assume valori positivi e negativi, perché elevando al quadrato ogni dato tutti i valori diventano positivi. Pertanto, la media quadratica viene utilizzata per analizzare variabili in cui non è importante il segno, ma il suo valore assoluto.

Ad esempio, la media quadratica viene utilizzata per studiare gli errori di misurazione, perché in questi casi non stiamo guardando se l’errore è positivo o negativo, ma piuttosto analizziamo l’entità dell’errore durante la misurazione.

Inoltre, i quadrati dei numeri grandi hanno valori molto più alti rispetto ai quadrati dei numeri piccoli, quindi nel quadrato centrale i numeri grandi sono più importanti dei numeri piccoli.

La media quadrata è un tipo di media statistica insieme alla media aritmetica, alla media ponderata, alla media geometrica e alla media armonica.

Vantaggi e svantaggi della radice quadrata media

La media quadratica presenta vantaggi e svantaggi rispetto ad altri tipi di medie.

Il vantaggio principale della media quadratica è che permette di ottenere un’ottima approssimazione del valore medio di una variabile discreta. D’altra parte, il grande svantaggio della media quadrata è che il suo calcolo è piuttosto complicato, poiché è necessario eseguire diverse operazioni.

Al contrario, la radice quadrata è molto utile per analizzare le misurazioni degli errori. Inoltre dà molta più importanza ai valori elevati, anche se questa proprietà implica che una misurazione errata altererà significativamente il risultato efficace.

Come calcolare la radice quadrata media

Per calcolare la radice quadrata media, è necessario eseguire i seguenti passaggi:

Calcolare il quadrato di ciascun dato statistico.
Somma tutti i quadrati calcolati nel passaggio precedente.
Dividere il risultato per il numero di elementi di dati nel campione.
Trova la radice quadrata del valore precedente.
Il risultato ottenuto è la media quadrata del campione statistico.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la radice quadrata media di qualsiasi set di dati.

Esempio quadrato medio

Una volta che sappiamo come ottenere la radice quadrata media, determineremo come esempio la radice quadrata media di un insieme di dati.

In una lezione di laboratorio universitaria, il professore chiede ai suoi studenti di fare un esperimento con sostanze chimiche. L’obiettivo dell’esperimento chimico è ottenere una soluzione di 3 litri in totale. I gruppi di studenti hanno ottenuto i seguenti dati:

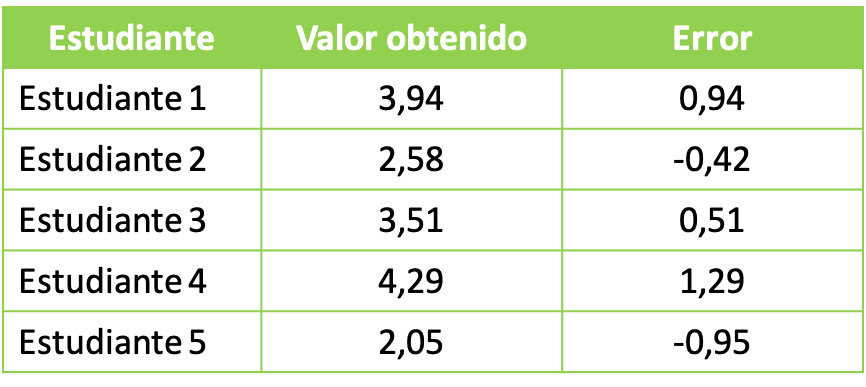
Per studiare i dati statistici ottenuti, si procede a calcolare il valore della media quadrata con l’errore ottenuto da ciascun gruppo. Applichiamo quindi la formula della media quadratica:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

E sostituiamo i dati nella formula e calcoliamo la radice quadrata media:

$\displaystyle RMS=\sqrt{\frac{0,94^2+(-0,42)^2+0,51^2+1,29^2+(-0,95)^2}{5}}=0,88$

Pertanto, l’errore medio ottenuto nell’esperimento, secondo la radice quadrata media, è di 0,88 litri.

Calcolatore del valore quadratico medio

Inserisci i dati di qualsiasi campione statistico nella seguente calcolatrice per calcolare la radice quadrata media. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più