Come eseguire un test di adattamento del chi quadrato in excel

Un test di bontà di adattamento chi quadrato viene utilizzato per determinare se una variabile categoriale segue o meno una distribuzione ipotetica.

Questo tutorial spiega come eseguire un test di bontà di adattamento chi quadrato in Excel.

Esempio: test di bontà di adattamento del chi quadrato in Excel

Il proprietario di un negozio afferma che un numero uguale di clienti si reca nel suo negozio ogni giorno della settimana. Per verificare questa ipotesi, un ricercatore indipendente registra il numero di clienti che entrano nel negozio in una determinata settimana e rileva quanto segue:

• Lunedì: 50 clienti
• Martedì: 60 clienti
• Mercoledì: 40 clienti
• Giovedì: 47 clienti
• Venerdì: 53 clienti

Utilizzeremo i seguenti passaggi per eseguire un test di bontà di adattamento del chi quadrato per determinare se i dati sono coerenti con l’affermazione del proprietario del negozio.

Passaggio 1: inserisci i dati.

Innanzitutto, inseriremo i valori dei dati per il numero previsto di clienti ogni giorno in una colonna e il numero osservato di clienti ogni giorno in un’altra colonna:

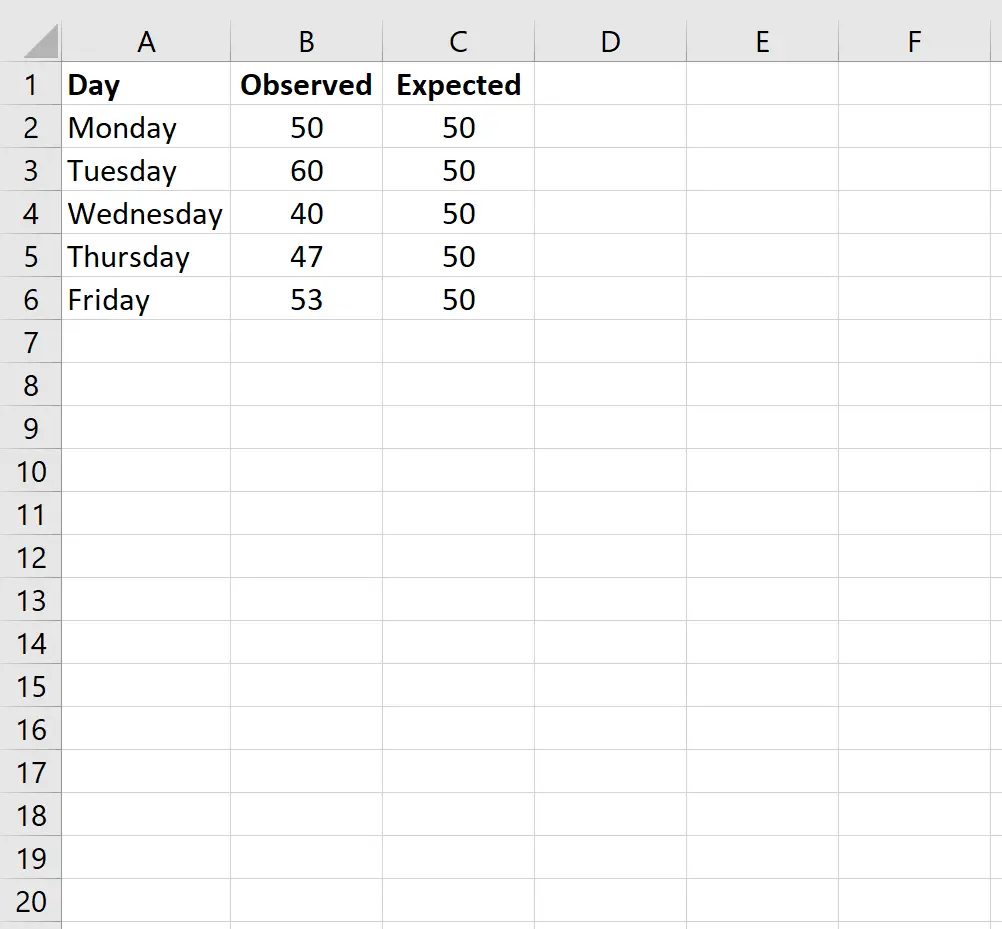
Nota: c’erano 250 clienti in totale. Pertanto, se il proprietario del negozio si aspetta che un numero uguale di clienti entri nel negozio ogni giorno, si aspetterebbe di avere 50 clienti al giorno.

Passaggio 2: trovare la differenza tra i valori osservati e attesi.

La statistica del test Chi-quadrato per il test della bontà di adattamento è X ² = Σ(OE) ² / E.

Oro:

• Σ: è un simbolo di fantasia che significa “somma”
• O: valore osservato
• E: valore atteso

La formula seguente mostra come calcolare (OE) ² /E per ciascuna riga:

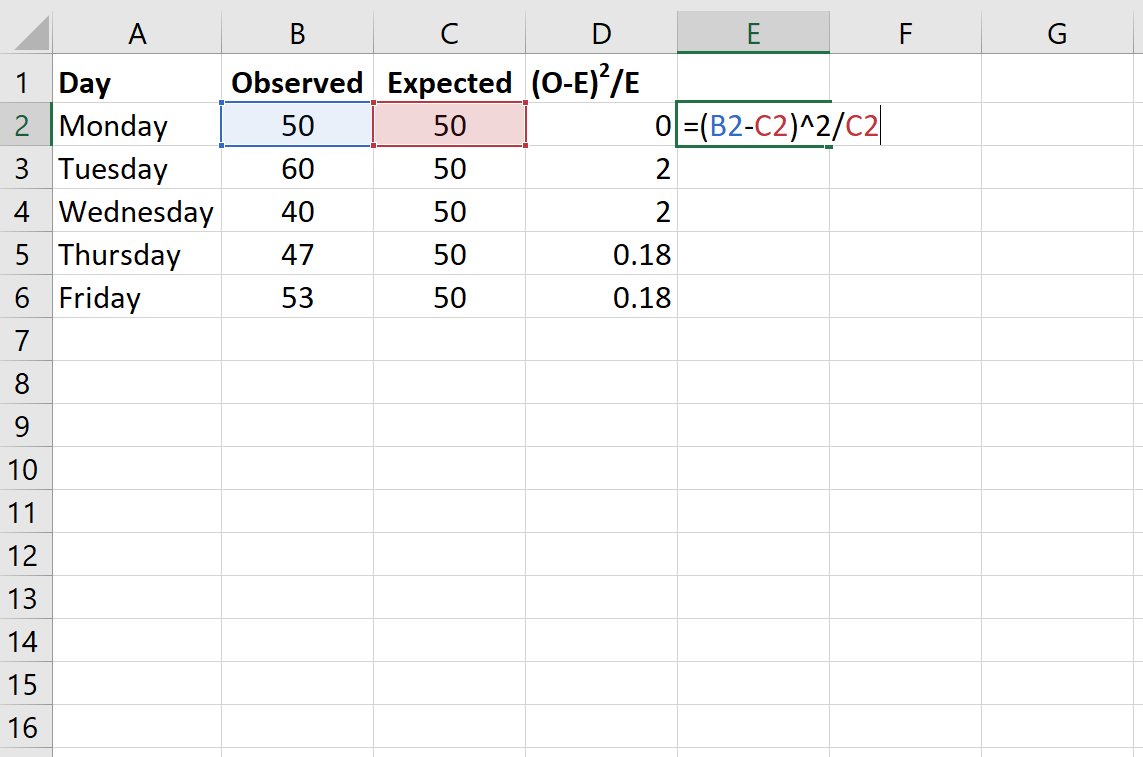
Passaggio 3: calcolare la statistica del test chi quadrato e il corrispondente valore p.

Infine, calcoleremo la statistica del test Chi-quadrato e il corrispondente valore p utilizzando le seguenti formule:

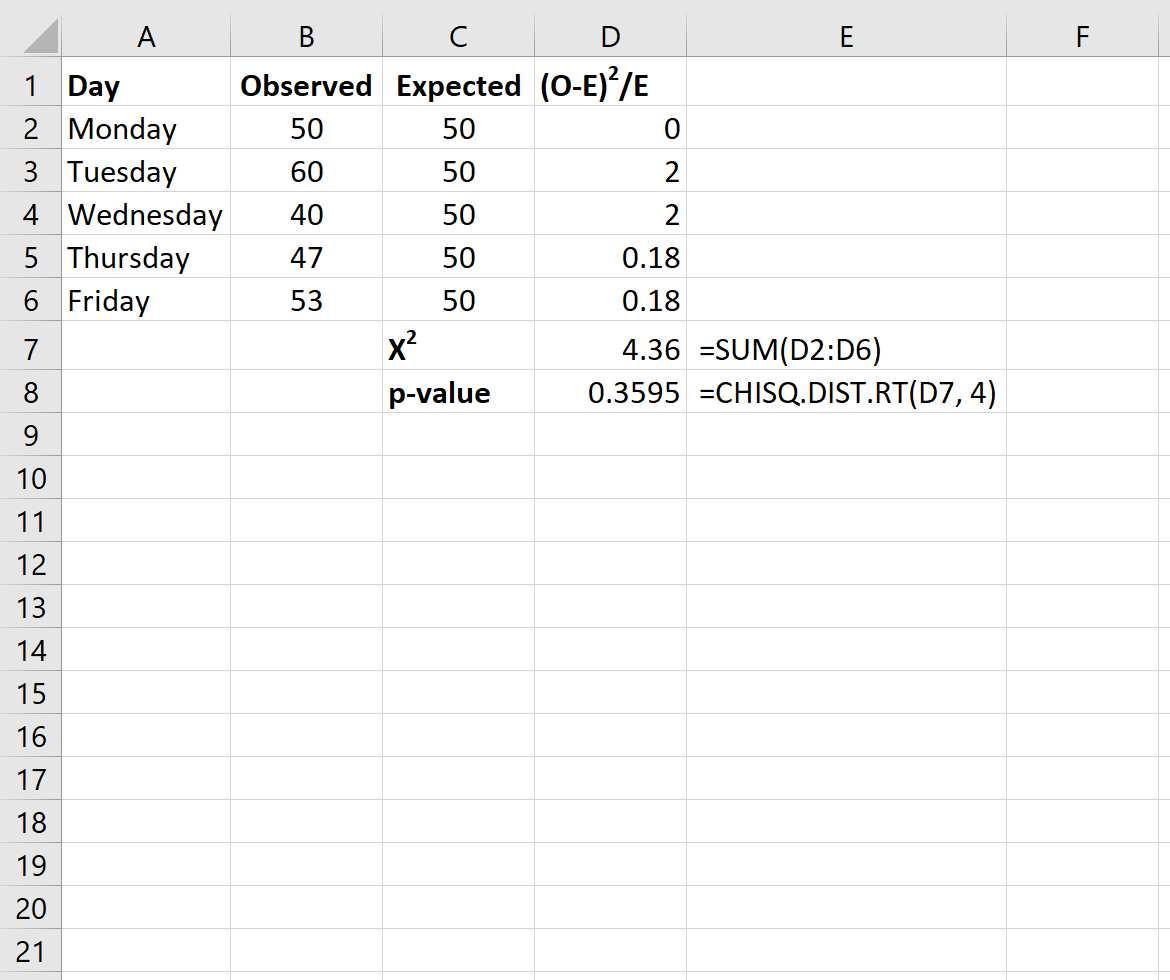
Nota: la funzione di Excel DISTRIB.Q.CHI.RT(x, gradi_libertà) restituisce la giusta probabilità della distribuzione Chi quadrato associata a una statistica test x e a un certo grado di libertà. I gradi di libertà sono calcolati come n-1. In questo caso, gradi_libertà = 5 – 1 = 4.

Passaggio 4: interpretare i risultati.

La statistica del test ^X2 per il test è 4,36 e il corrispondente valore p è 0,3595 . Poiché questo valore p non è inferiore a 0,05, non riusciamo a rifiutare l’ipotesi nulla. Ciò significa che non abbiamo prove sufficienti per affermare che la reale distribuzione dei clienti sia diversa da quella riportata dal proprietario del negozio.