Quando dovresti utilizzare un box plot? (3 scenari)

Un box plot è un tipo di grafico che visualizza il riepilogo di cinque cifre di un set di dati, che include:

• Il valore minimo
• Il primo quartile (il 25° percentile)
• Il valore mediano
• Il terzo quartile (il 75° percentile)
• Il valore massimo

Utilizziamo tre semplici passaggi per creare un box plot per qualsiasi set di dati:

• 1. Disegna una casella dal primo al terzo quartile
• 2. Traccia una linea verticale in corrispondenza della mediana
• 3. Disegna i “baffi” dei quartili sul valore minimo e massimo

In genere creiamo boxplot in uno dei tre scenari:

Scenario 1: visualizza la distribuzione dei valori in un set di dati.

Un box plot ci consente di visualizzare rapidamente la distribuzione dei valori in un set di dati e vedere dove si trovano i cinque valori numerici di riepilogo.

Scenario 2: confrontare due o più distribuzioni.

I boxplot affiancati ci consentono di visualizzare le differenze tra due o più distribuzioni e confrontare i valori mediani e la distribuzione dei valori tra le distribuzioni.

Scenario 3: identificare i valori anomali.

Nei grafici a scatola, i valori anomali sono solitamente rappresentati da piccoli cerchi che si estendono oltre ciascun baffo. Un’osservazione è definita outlier se soddisfa uno dei seguenti criteri:

• Un’osservazione è inferiore a Q1 – 1,5*(intervallo interquartile)
• Un’osservazione è maggiore di Q3 + 1,5*(intervallo interquartile)

Creando un box plot, possiamo vedere rapidamente se una distribuzione presenta o meno valori anomali.

Gli esempi seguenti mostrano come utilizzeremmo un box plot in ogni scenario.

Scenario 1: visualizza la distribuzione dei valori in un set di dati

Supponiamo che un allenatore di basket voglia visualizzare la distribuzione dei punti segnati dai giocatori della sua squadra e quindi crei il seguente box plot:

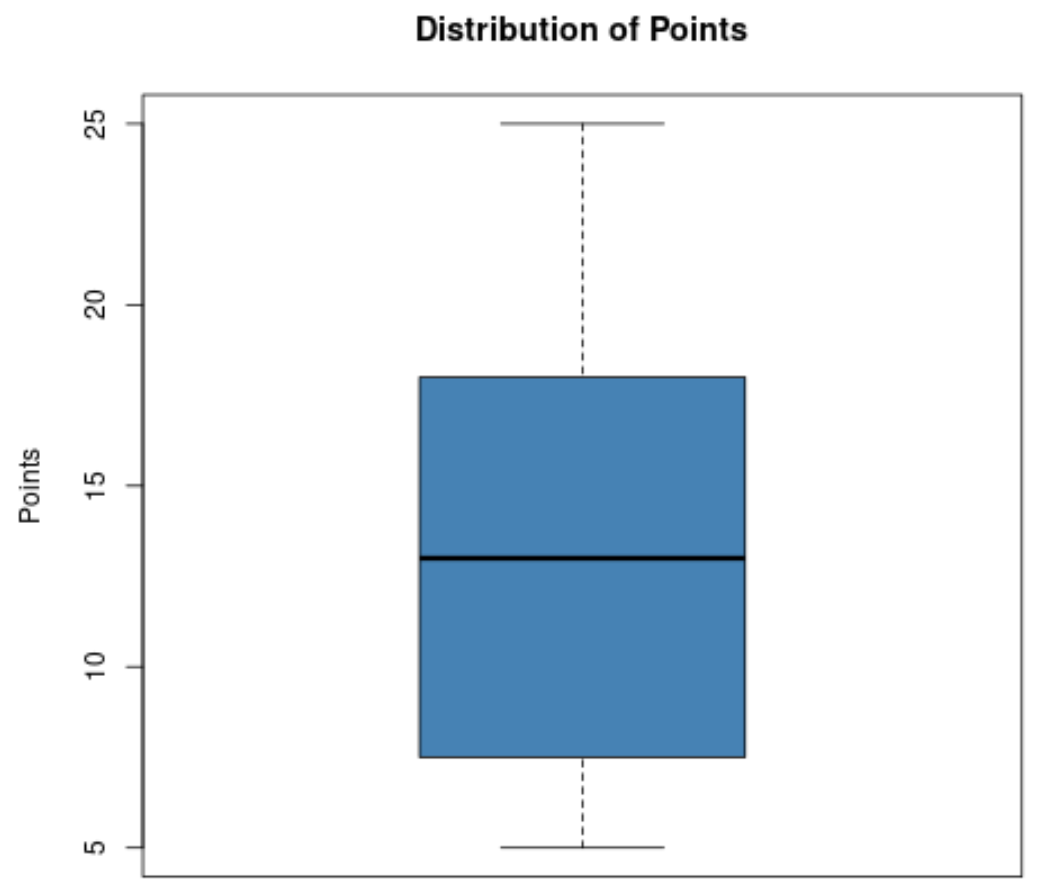
Sulla base di questo box plot, può vedere rapidamente i seguenti valori:

• Minimo: 5
• T1 (primo quartile): circa 8
• Media: circa 13
• T3 (terzo quartile): circa 18
• Massimo: 25

Ciò consente all’allenatore di vedere rapidamente che i punti segnati dai giocatori vanno da 5 a 25, che la media dei punti segnati è di circa 13 e che il 50% dei suoi giocatori segna tra circa 8 e 18 punti a partita.

Scenario 2: confronta due o più distribuzioni

Supponiamo che un analista sportivo voglia confrontare la distribuzione dei punti segnati dai giocatori di basket di tre squadre diverse e crei i seguenti box plot:

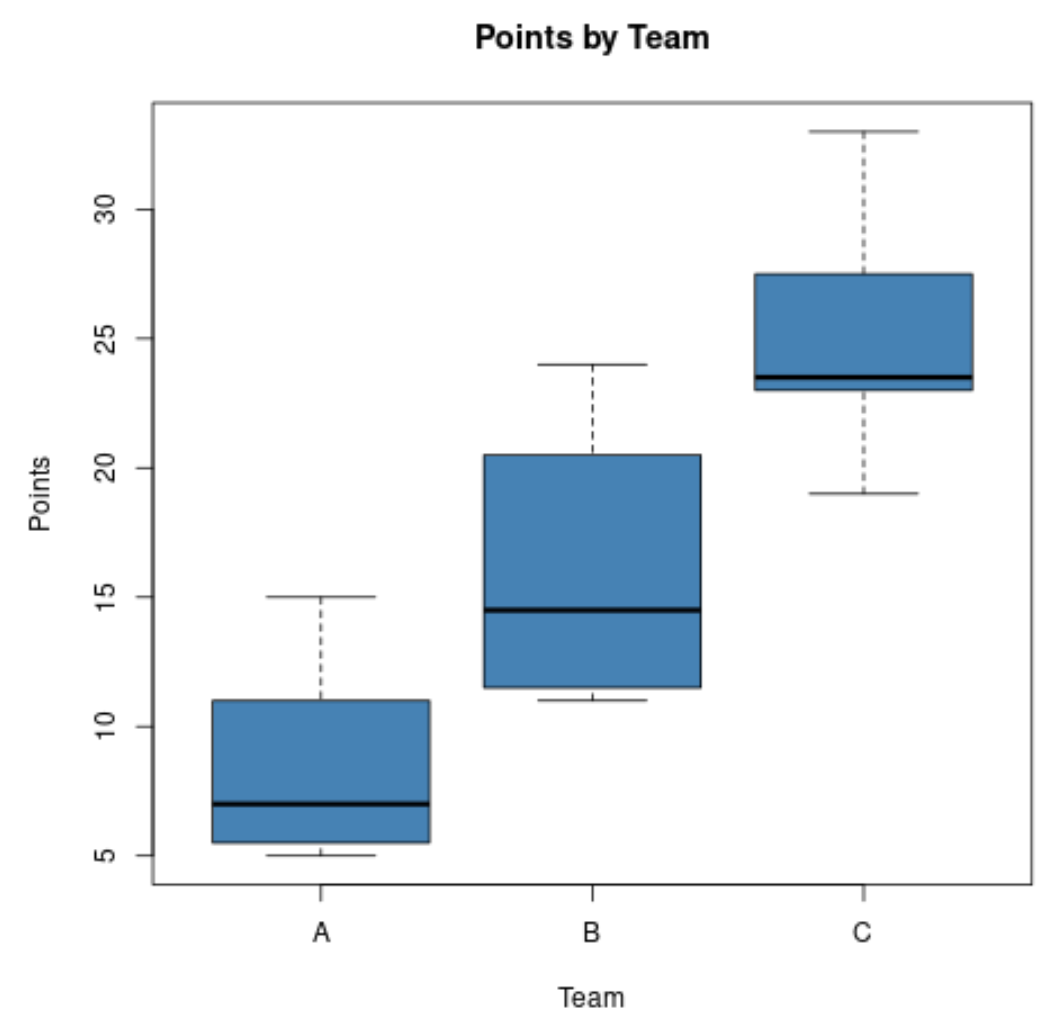
Utilizzando questi grafici, può vedere rapidamente che la squadra C ha ottenuto i punti medi più alti e la squadra A ha ottenuto i punti medi più bassi.

Può anche vedere rapidamente che la squadra B ha la più ampia distribuzione di punti segnati poiché il box plot della squadra B ha il riquadro più lungo.

Scenario 3: identificare i valori anomali

Supponiamo che un allenatore di basket voglia sapere se uno dei suoi giocatori è un valore anomalo in termini di punti segnati. Decide di creare il seguente box plot per visualizzare la distribuzione dei punti segnati dai suoi giocatori:

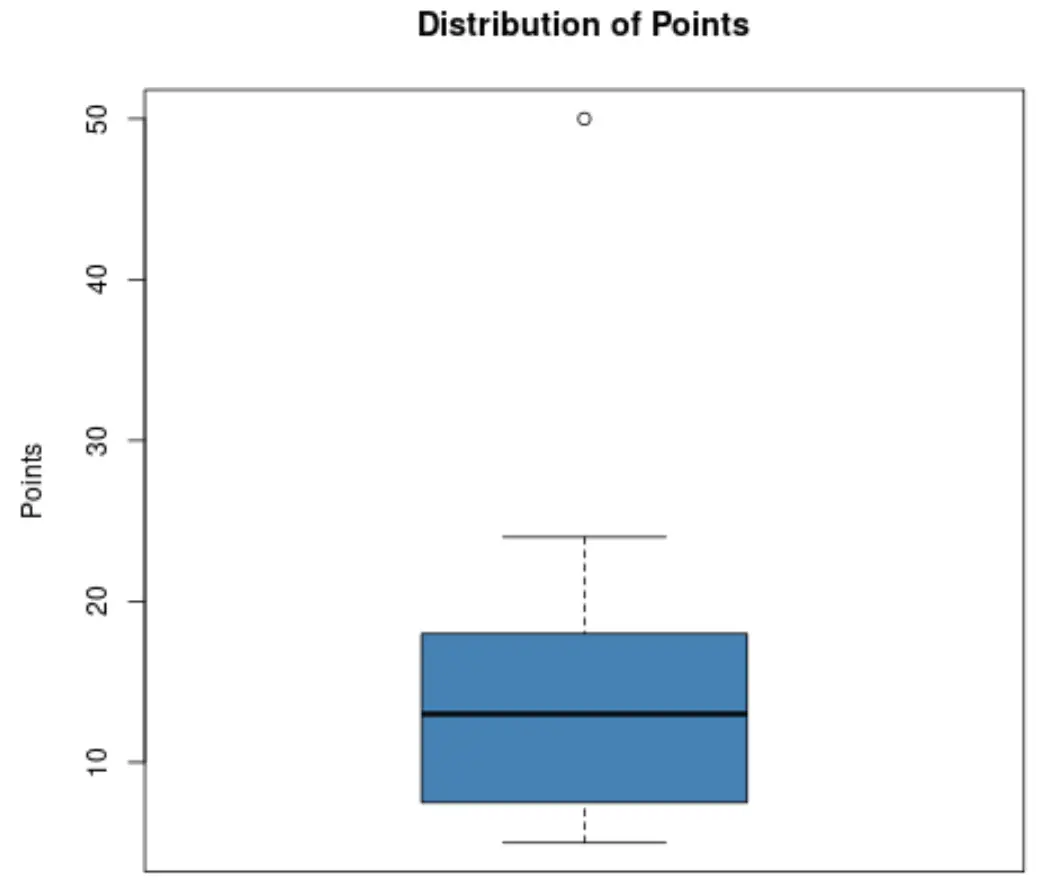
Usando questo grafico, l’allenatore può vedere che il piccolo punto nella parte superiore del grafico indica un valore anomalo.

Nello specifico, uno dei giocatori ha segnato circa 50 punti, un valore considerato anomalo rispetto a tutti gli altri punti segnati.

Risorse addizionali

I seguenti tutorial offrono spiegazioni dettagliate su come utilizzare i boxplot nella pratica:

Come trovare l’intervallo interquartile (IQR) di un box plot
Come identificare l’asimmetria nei box plot
Come confrontare i box plot

I seguenti tutorial spiegano come creare box plot in diversi software statistici:

Come creare un diagramma a scatola in Fogli Google
Come creare box plot in SPSS
Come creare box plot affiancati in Excel
Come creare box plot affiancati in R