Quando dovresti usare la correlazione? (spiegazione ed esempi)

La correlazione viene utilizzata per misurare l’associazione lineare tra due variabili.

Un coefficiente di correlazione assume sempre un valore compreso tra -1 e 1 dove:

• -1 indica una correlazione lineare perfettamente negativa tra due variabili
• 0 indica alcuna correlazione lineare tra due variabili
• 1 indica una correlazione lineare perfettamente positiva tra due variabili

Una domanda che spesso gli studenti pongono è: quando dovrei usare la correlazione?

La risposta breve: utilizzare la correlazione quando si desidera quantificare la relazione lineare tra due variabili e nessuna delle due variabili rappresenta una risposta o una variabile di “risultato” .

Gli esempi seguenti illustrano quando è opportuno e quando non è opportuno utilizzare la correlazione nella pratica.

Esempio 1: quando utilizzare la correlazione

Supponiamo che un professore voglia comprendere la relazione lineare tra i punteggi dei test di matematica e i punteggi dei test di scienze degli studenti della sua classe.

Ad esempio, gli studenti che ottengono buoni risultati nell’esame di matematica ottengono buoni risultati anche nell’esame di scienze? Oppure gli studenti che ottengono punteggi alti in matematica tendono ad avere punteggi bassi in scienze?

In questo scenario, potrebbe calcolare la correlazione tra i punteggi degli esami di matematica e quelli degli esami di scienze perché vuole solo comprendere la relazione lineare tra le due variabili e nessuna delle due variabili può essere considerata una variabile di risposta.

Supponiamo che calcoli il coefficiente di correlazione di Pearson e trovi che è r = 0,78. Si tratta di una forte correlazione positiva, nel senso che gli studenti che ottengono buoni risultati in matematica tendono ad avere buoni risultati anche in scienze.

Esempio 2: quando non utilizzare la correlazione

Supponiamo che il reparto marketing di un’azienda voglia quantificare l’impatto della spesa pubblicitaria sulle entrate totali.

Ad esempio, per ogni dollaro aggiuntivo speso in pubblicità, quante entrate aggiuntive può aspettarsi di guadagnare l’azienda?

In questo scenario, il dipartimento deve utilizzare un modello di regressione lineare per quantificare la relazione tra la spesa pubblicitaria e le entrate totali, poiché la variabile “entrate” è la variabile di risposta.

Supponiamo che il dipartimento applichi un semplice modello di regressione lineare e scopra che la seguente equazione descrive meglio la relazione tra la spesa pubblicitaria e le entrate totali:

Entrate totali = 145,4 + 0,34*(spese pubblicitarie)

Interpreteremmo ciò nel senso che ogni dollaro aggiuntivo speso in pubblicità si traduce in un aumento medio di 0,34 dollari nelle entrate totali.

Precauzioni per l’uso della correlazione

È importante notare che la correlazione può essere utilizzata solo per quantificare la relazione lineare tra due variabili.

Tuttavia, in determinate circostanze, un coefficiente di correlazione non sarà in grado di catturare efficacemente una relazione tra due variabili che condividono una relazione non lineare.

Ad esempio, supponiamo di creare il seguente grafico a dispersione per visualizzare la relazione tra due variabili:

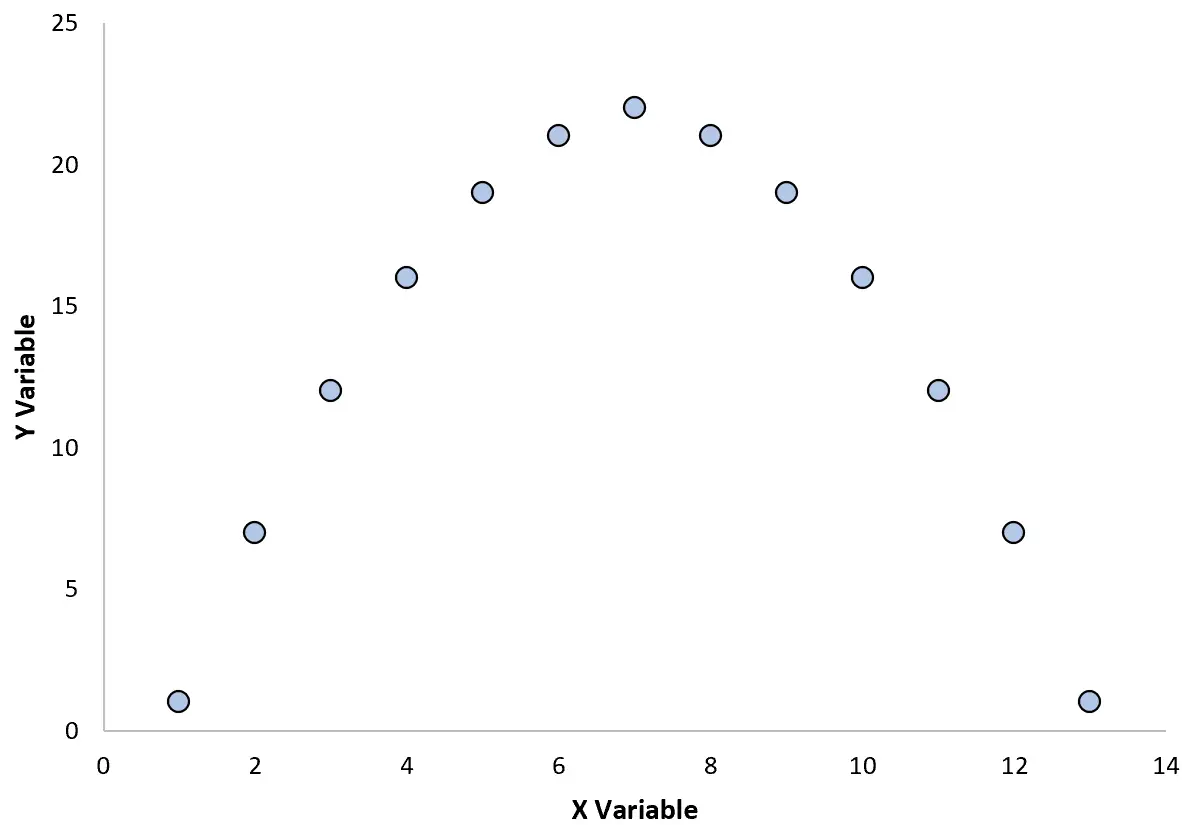
Se calcoliamo il coefficiente di correlazione tra queste due variabili, risulta essere r = 0. Ciò significa che non esiste una relazione lineare tra le due variabili.

Tuttavia, dal grafico possiamo vedere che le due variabili hanno effettivamente una relazione: si tratta semplicemente di una relazione quadratica invece che di una relazione lineare.

Quindi, quando calcoli la correlazione tra due variabili, tieni presente che può essere utile anche creare un grafico a dispersione per visualizzare la relazione tra le variabili.

Anche se due variabili non hanno una relazione lineare, è possibile che abbiano una relazione non lineare che verrebbe rivelata in un grafico a dispersione.

Risorse addizionali

I seguenti tutorial spiegano più in dettaglio come viene utilizzata la correlazione in diverse circostanze:

6 esempi di correlazione nella vita reale
Cos’è considerata una correlazione “forte”?
Correlazione vs. associazione: qual è la differenza?
Correlazione vs regressione: qual è la differenza?