Quando utilizzare la correlazione del rango di spearman (2 scenari)

Il modo più comune per quantificare l’associazione lineare tra due variabili è utilizzare il coefficiente di correlazione di Pearson , che assume sempre un valore compreso tra -1 e 1 dove:

• -1 indica una correlazione lineare perfettamente negativa
• 0 indica alcuna correlazione lineare
• 1 indica una correlazione lineare perfettamente positiva

Tuttavia, questo tipo di coefficiente di correlazione funziona meglio quando la vera relazione sottostante tra le due variabili è lineare .

Esiste un altro tipo di coefficiente di correlazione chiamato correlazione dei ranghi di Spearman che è meglio utilizzato in due scenari specifici:

Scenario 1 : quando si lavora con dati classificati.

• Un esempio potrebbe essere un set di dati contenente la classifica del punteggio dell’esame di matematica di uno studente, nonché la classifica del punteggio dell’esame di scienze in una classe.

Scenario 2 : quando sono presenti uno o più valori anomali estremi.

• Quando in un set di dati sono presenti valori anomali estremi, il coefficiente di correlazione di Pearson ne risente notevolmente.

Gli esempi seguenti mostrano come calcolare la correlazione del rango di Spearman in ciascuno di questi scenari.

Scenario 1: correlazione della classifica dei lancieri con i dati classificati

Considera il seguente set di dati (e il corrispondente diagramma a dispersione) che mostra la relazione tra due variabili:

Utilizzando un software statistico, possiamo calcolare i seguenti coefficienti di correlazione per queste due variabili:

• Correlazione di Pearson: 0,79
• Correlazione del rango di Spearman: 1

In questo scenario, se ci preoccupiamo solo del rango dei valori dei dati (all’aumentare del rango di x, aumenta anche il rango di y?), allora la correlazione dei ranghi di Spearman ci darebbe un’idea migliore del correlazione tra le due variabili. .

In questo particolare set di dati, all’aumentare del rango di x, aumenta sempre il rango di y.

La correlazione dei ranghi di Spearman cattura perfettamente questo comportamento dicendoci che esiste una relazione positiva perfetta ( ρ = 1 ) tra i ranghi di x e i ranghi di y.

D’altra parte, la correlazione di Pearson ci dice che esiste una forte relazione lineare ( r = 0,79 ) tra le due variabili.

Questo è vero, ma non è utile se ci interessa solo la relazione tra i ranghi di x e i ranghi di y.

Scenario 2: correlazione della classifica di Spearman con valori anomali estremi

Considera il seguente set di dati (e il corrispondente diagramma a dispersione) che mostra la relazione tra due variabili:

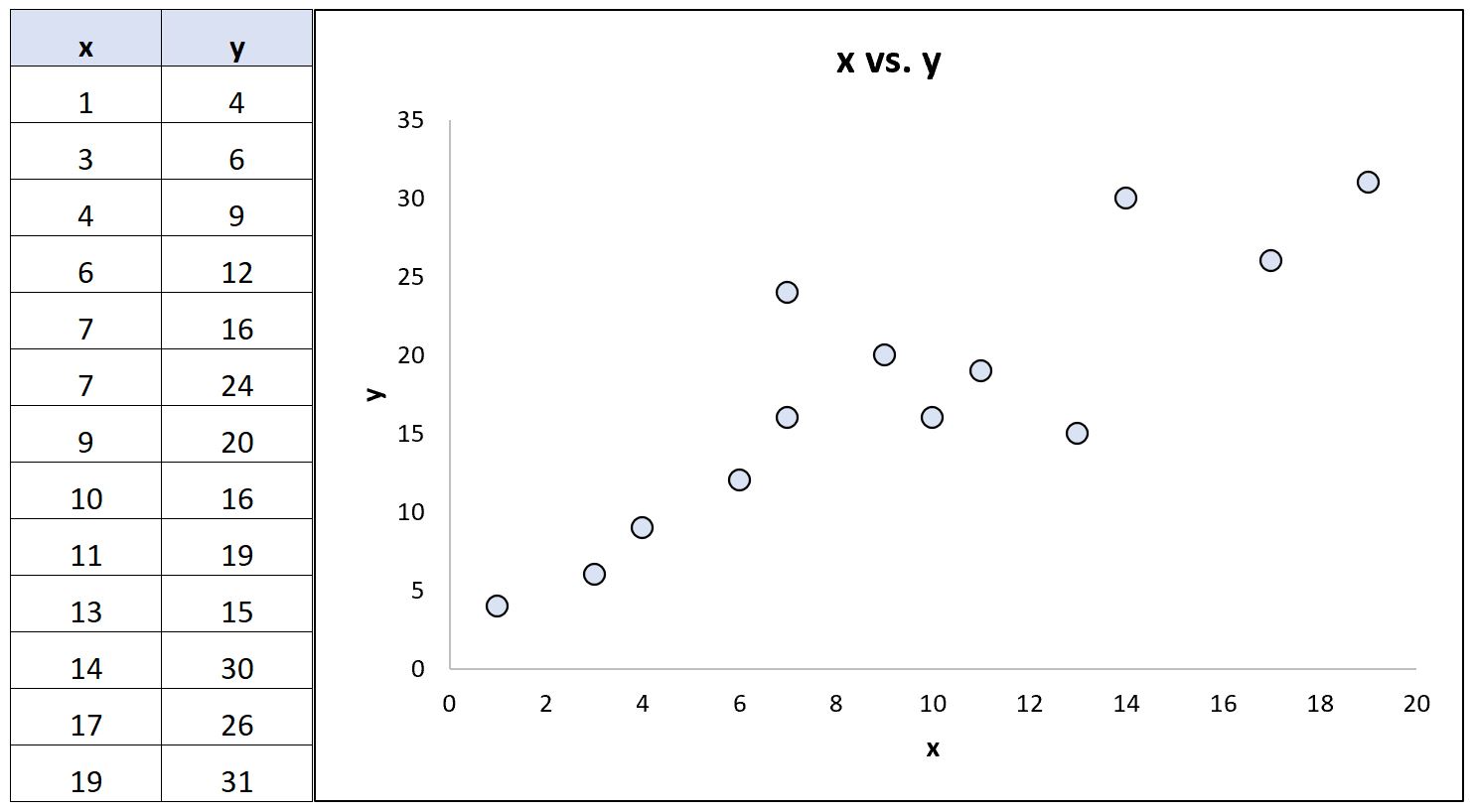
Utilizzando un software statistico, possiamo calcolare i seguenti coefficienti di correlazione per queste due variabili:

• Correlazione di Pearson: 0,86
• Correlazione del grado di Spearman: 0,85

I coefficienti di correlazione sono quasi identici perché la relazione sottostante tra le variabili è approssimativamente lineare e non ci sono valori anomali estremi.

Supponiamo ora di modificare l’ultimo valore y nel set di dati in modo che diventi un valore anomalo estremo:

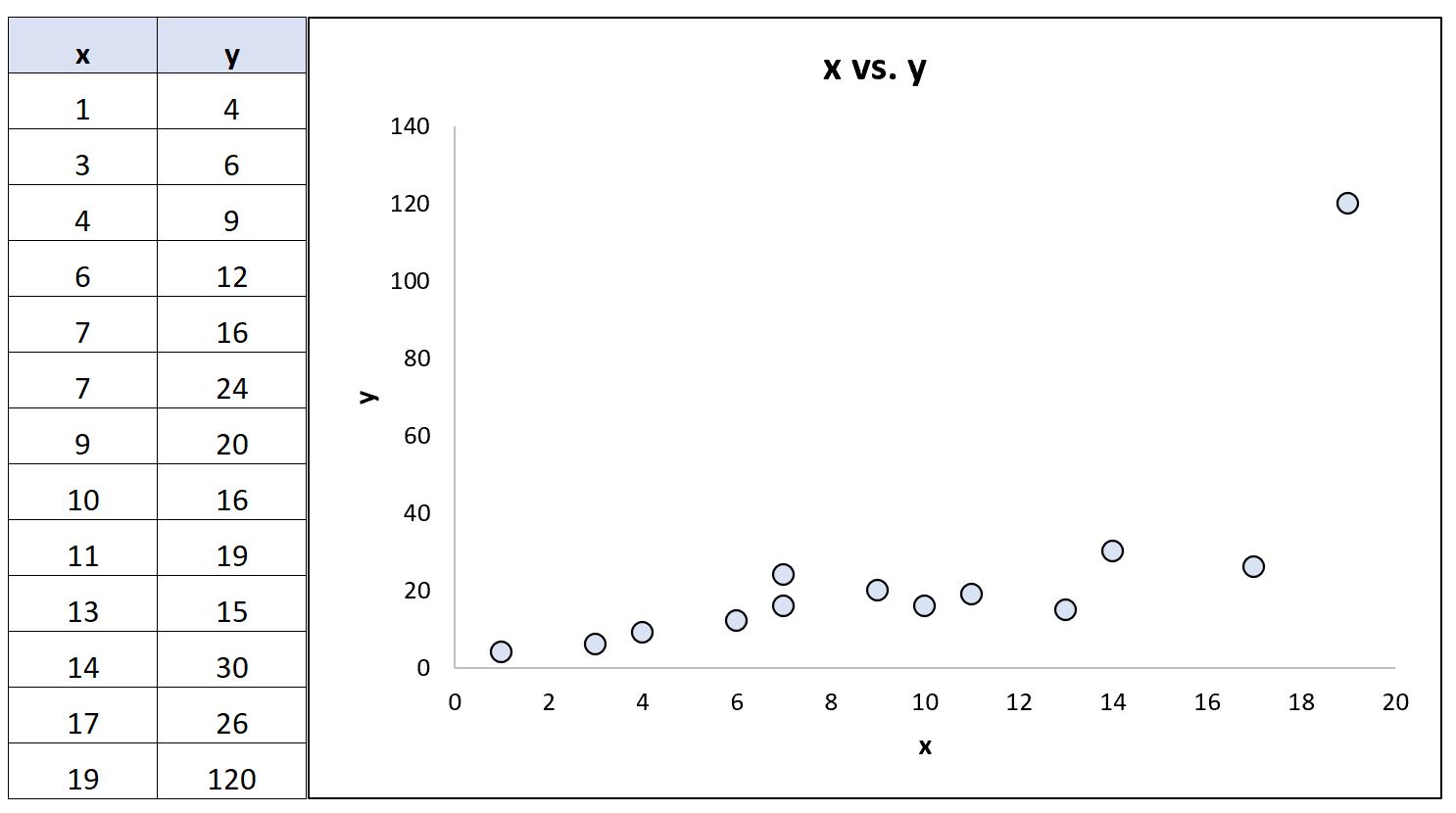
Utilizzando un software statistico, possiamo ricalcolare i coefficienti di correlazione:

• Correlazione di Pearson: 0,69
• Correlazione del grado di Spearman: 0,85

Il coefficiente di correlazione di Pearson è cambiato in modo significativo mentre il coefficiente di correlazione del rango di Spearman è rimasto lo stesso.

Usando il gergo statistico, diremmo che la relazione tra x e y è monotona (all’aumentare di x, y generalmente aumenta) ma non lineare poiché l’outlier influenza notevolmente i dati.

In questo scenario, la correlazione per ranghi di Spearman quantifica bene questa relazione monotona, mentre la correlazione di Pearson fa un pessimo lavoro perché tenta di calcolare la relazione lineare tra le due variabili.

Correlato: Come segnalare la correlazione del rango Spearman in formato APA

Risorse addizionali

I seguenti tutorial spiegano come calcolare la correlazione dei ranghi di Spearman utilizzando diversi software:

Come calcolare la correlazione del rango di Spearman in Excel
Come calcolare la correlazione del rango di Spearman in Fogli Google
Come calcolare la correlazione del rango di Spearman in R
Come calcolare la correlazione del rango di Spearman in Python