Quando utilizzare la regressione ridge e lazo

Nella regressione lineare multipla ordinaria, utilizziamo un insieme di variabili predittive p e una variabile di risposta per adattare un modello della forma:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

I valori di β ₀ , β ₁ , B ₂ , …, β _p sono scelti utilizzando il metodo dei minimi quadrati, che minimizza la somma dei quadrati dei residui (RSS):

RSS = Σ(y _i – ŷ _i ) ²

Oro:

• Σ : Un simbolo che significa “somma”
• y _i : il valore di risposta effettivo per l’ ^i-esima osservazione
• ŷ _i : il valore di risposta previsto per l’ ^iesima osservazione

Il problema della multicollinearità nella regressione

Un problema che spesso si presenta nella pratica con la regressione lineare multipla è la multicollinearità , ovvero quando due o più variabili predittive sono altamente correlate tra loro, in modo tale da non fornire informazioni univoche o indipendenti nel modello di regressione.

Ciò può rendere inaffidabili le stime dei coefficienti del modello e presentare una varianza elevata. Cioè, quando il modello viene applicato a un nuovo set di dati mai visto prima, è probabile che funzioni in modo scarso.

Evitare la multicollinearità: regressione Ridge e Lasso

Due metodi che possiamo utilizzare per aggirare questo problema di multicollinearità sono la regressione della cresta e la regressione del lazo .

La regressione della cresta cerca di minimizzare quanto segue:

• RSS + λΣβ _j ²

La regressione lazo cerca di minimizzare quanto segue:

• RSS + λΣ|β _j |

In entrambe le equazioni, il secondo termine è chiamato penalità di ritiro .

Quando λ = 0, questo termine di penalità non ha alcun effetto e la regressione della cresta e la regressione del lazo producono le stesse stime dei coefficienti dei minimi quadrati.

Tuttavia, quando λ si avvicina all’infinito, la penalità di contrazione diventa più influente e le variabili predittive che non sono importabili nel modello diminuiscono verso zero.

Con la regressione Lasso, è possibile che alcuni coefficienti diventino completamente pari a zero quando λ diventa sufficientemente grande.

Vantaggi e svantaggi della regressione Ridge e Lasso

Il vantaggio della regressione Ridge e Lasso rispetto alla regressione dei minimi quadrati è il compromesso bias-varianza .

Ricordiamo che l’errore quadratico medio (MSE) è una metrica che possiamo utilizzare per misurare l’accuratezza di un determinato modello e viene calcolata come segue:

MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE = Varianza + Bias ² + Errore irriducibile

L’idea di base della regressione Ridge e della regressione Lasso è quella di introdurre una piccola distorsione in modo che la varianza possa essere significativamente ridotta, portando a un MSE complessivo inferiore.

Per illustrare ciò, si consideri il seguente grafico:

Si noti che all’aumentare di λ, la varianza diminuisce in modo significativo con un aumento molto piccolo della distorsione. Tuttavia, oltre un certo punto, la varianza diminuisce meno rapidamente e la diminuzione dei coefficienti porta ad una loro significativa sottostima, che porta ad un forte aumento della distorsione.

Possiamo vedere dal grafico che l’MSE del test è più basso quando scegliamo un valore per λ che produca un compromesso ottimale tra bias e varianza.

Quando λ = 0, il termine di penalità nella regressione con lazo non ha alcun effetto e quindi produce le stesse stime dei coefficienti dei minimi quadrati. Tuttavia, aumentando λ fino a un certo punto, possiamo ridurre l’MSE complessivo del test.

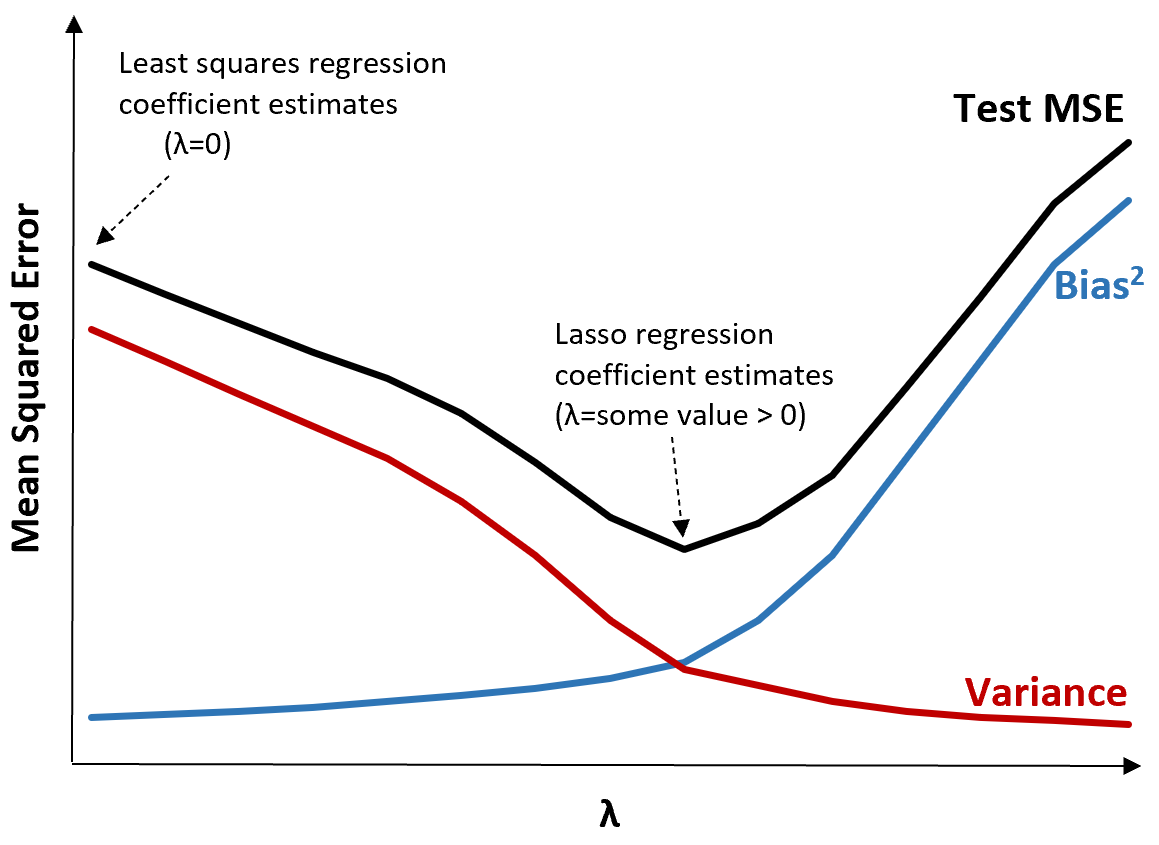
Ciò significa che l’adattamento del modello mediante la regressione ridge e lazo può potenzialmente produrre errori di test più piccoli rispetto all’adattamento del modello mediante la regressione dei minimi quadrati.

Lo svantaggio della regressione Ridge e Lasso è che diventa difficile interpretare i coefficienti nel modello finale man mano che si riducono verso lo zero.

Pertanto, la regressione Ridge e Lasso dovrebbe essere utilizzata quando si desidera ottimizzare la capacità predittiva anziché l’inferenza.

Cresta vs. Regressione lazo: quando utilizzarli ciascuno

La regressione del lasso e la regressione della cresta sono noti come metodi di regolarizzazione perché entrambi tentano di ridurre al minimo la somma residua dei quadrati (RSS) nonché un determinato termine di penalità.

In altre parole, vincolano o regolarizzano le stime dei coefficienti del modello.

Ciò solleva naturalmente la domanda: è migliore la regressione della cresta o del lazo?

Nei casi in cui solo un numero limitato di variabili predittive sono significative, la regressione lazo tende a funzionare meglio perché è in grado di ridurre completamente a zero le variabili insignificanti e rimuoverle dal modello.

Tuttavia, quando molte variabili predittive sono significative nel modello e i relativi coefficienti sono approssimativamente uguali, la regressione ridge tende a funzionare meglio perché mantiene tutti i predittori nel modello.

Per determinare quale modello è il migliore per fare previsioni, in genere eseguiamo una convalida incrociata k-fold e scegliamo il modello che produce l’errore quadratico medio radice del test più basso.

Risorse addizionali

Le seguenti esercitazioni forniscono un’introduzione alla regressione Ridge e alla regressione lazo:

• Introduzione alla regressione della cresta
• Introduzione alla regressione lazo

I seguenti tutorial spiegano come eseguire entrambi i tipi di regressione in R e Python:

• Regressione della cresta in R
• Regressione della cresta in Python
• Regressione al lazo in R
• Regressione lazo in Python