Quando dovresti usare la regressione polinomiale?

La regressione polinomiale è una tecnica che possiamo utilizzare per adattare un modello di regressione quando la relazione tra le variabili predittive e la variabile di risposta non è lineare.

Un modello di regressione polinomiale assume la forma seguente:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

In pratica, ci sono tre semplici modi per determinare se utilizzare la regressione polinomiale rispetto a un modello più semplice come la regressione lineare .

1. Creare un grafico a dispersione della variabile predittore e della variabile risposta

Il modo più semplice per determinare se utilizzare la regressione polinomiale è creare un semplice grafico a dispersione della variabile predittore e della variabile di risposta.

Ad esempio, supponiamo di voler utilizzare la variabile predittore “ore di studio” per prevedere il voto che uno studente riceverà all’esame finale.

Prima di adattare un modello di regressione, possiamo creare un grafico a dispersione delle ore studiate rispetto ai risultati dell’esame. Supponiamo che il nostro grafico a dispersione sia simile al seguente:

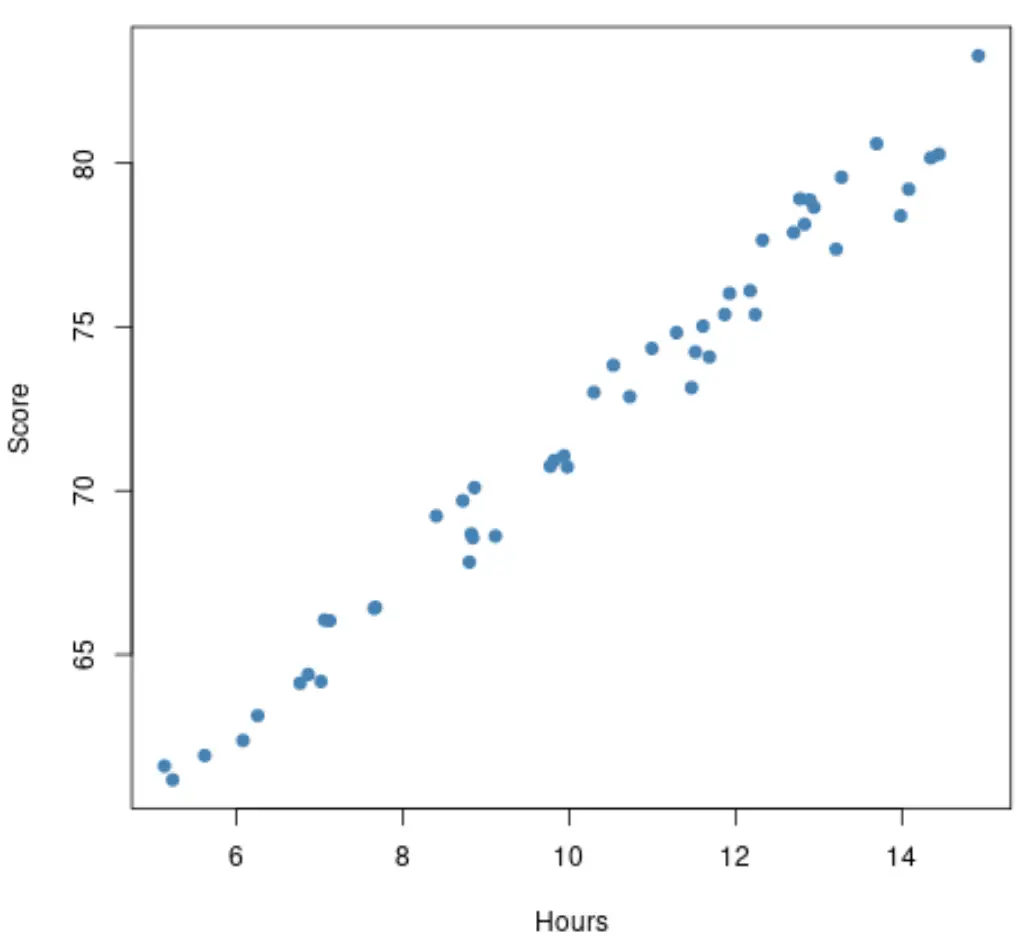
La relazione tra le ore studiate e i risultati degli esami appare lineare , quindi avrebbe senso adattare un semplice modello di regressione lineare a questo set di dati.

Tuttavia, supponiamo che il grafico a dispersione sia effettivamente simile al seguente:

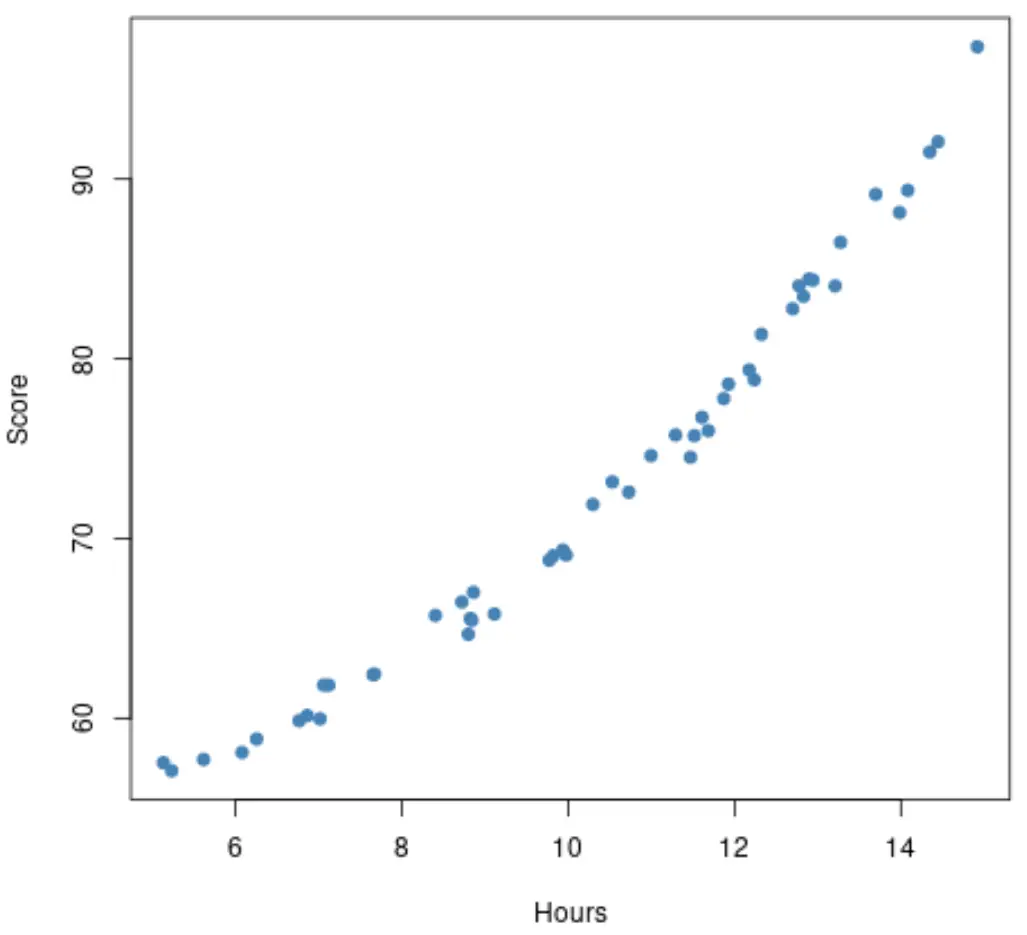
Questa relazione sembra un po’ più non lineare , il che ci dice che potrebbe essere saggio adattare invece un modello di regressione polinomiale.

2. Creare un grafico dei valori adattati e residui

Un altro modo per determinare se è necessario utilizzare la regressione polinomiale è adattare un modello di regressione lineare al set di dati e quindi creare un grafico dei valori adattati rispetto ai residui del modello.

Se esiste una chiara tendenza non lineare nei residui, ciò indica che la regressione polinomiale potrebbe fornire un adattamento migliore ai dati.

Ad esempio, supponiamo di adattare un modello di regressione lineare utilizzando le ore studiate come variabile predittrice e il punteggio dell’esame come variabile di risposta, quindi creare il seguente grafico di valori adattati rispetto ai residui:

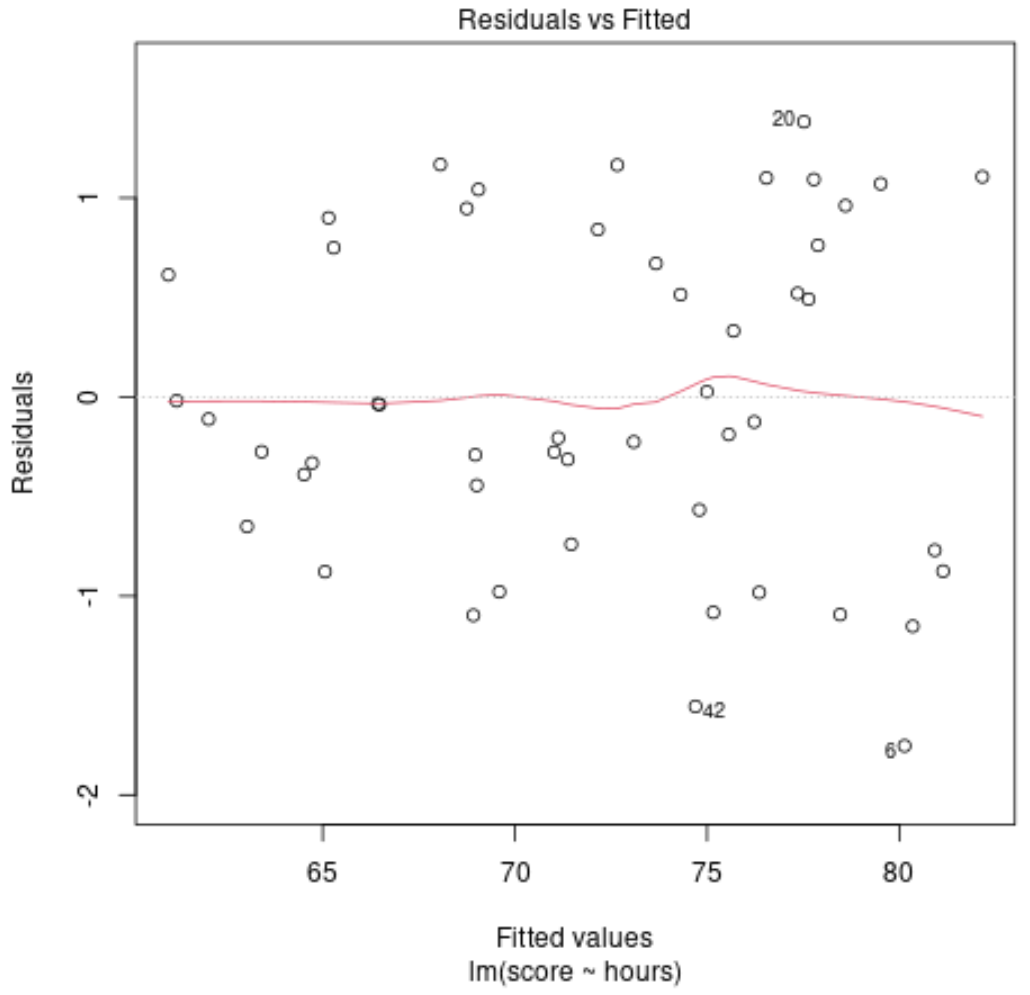
I residui sono sparsi in modo casuale attorno allo zero senza uno schema chiaro, indicando che un modello lineare fornisce un adattamento appropriato ai dati.

Tuttavia, supponiamo che il nostro grafico dei valori adattati rispetto ai residui sia effettivamente simile al seguente:

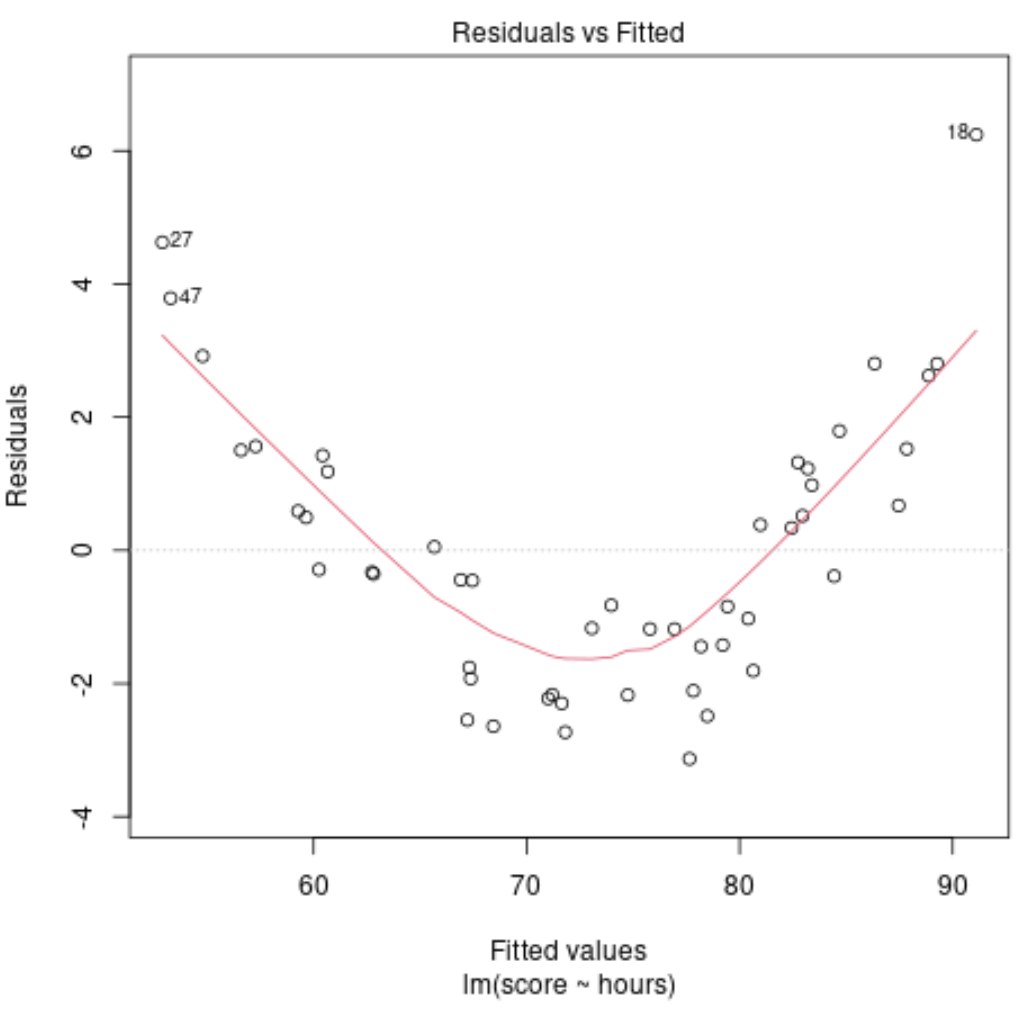
Dal grafico, possiamo vedere che esiste un chiaro modello non lineare nei residui: i residui presentano una forma a “U”.

Questo ci dice che un modello lineare non è appropriato per questi dati particolari e che potrebbe essere saggio adattare invece un modello di regressione polinomiale.

3. Calcolare il valore R quadrato corretto del modello

Un altro modo per determinare se utilizzare la regressione polinomiale è adattare sia un modello di regressione lineare che un modello di regressione polinomiale e calcolare i valori R quadrati adattati per entrambi i modelli.

L’R quadrato corretto rappresenta la proporzione della varianza nella variabile di risposta che può essere spiegata dalle variabili predittive nel modello, corretta per il numero di variabili predittive nel modello.

Il modello con il quadrato R corretto più alto rappresenta il modello che è in grado di utilizzare al meglio le variabili predittive per spiegare la variazione nella variabile di risposta.

Risorse addizionali

I seguenti tutorial spiegano come eseguire la regressione polinomiale utilizzando diversi software statistici:

Un’introduzione alla regressione polinomiale
Come eseguire la regressione polinomiale in R
Come eseguire la regressione polinomiale in Python
Come eseguire la regressione polinomiale in Excel