Quartili

Di Benjamin anderson Agosto 5, 2023 Statistiche 0 commenti

In questo articolo spieghiamo cosa sono i quartili. Troverai la definizione di ogni quartile, come calcolarli e diversi esempi concreti. Ti mostriamo anche come calcolare i quartili per i dati raggruppati. Inoltre, sarai in grado di calcolare i quartili di qualsiasi set di dati con un calcolatore online.

Cosa sono i quartili?

In statistica i quartili sono i tre valori che dividono un insieme di dati ordinati in quattro parti uguali. Pertanto, il primo, il secondo e il terzo quartile rappresentano rispettivamente il 25%, 50% e 75% di tutti i dati statistici.

I quartili sono rappresentati da una Q maiuscola e dall’indice quartile, quindi il primo quartile è Q ₁ , il secondo quartile è Q ₂ e il terzo quartile è Q ₃ .

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare i quartili di qualsiasi set di dati.

Va notato che i quartili sono una misura della posizione non centrale allo stesso modo dei quintili, dei decili e dei percentili. Puoi verificare cosa rappresenta ciascuno di questi tipi quantili in questa pagina web.

primo quartile

Il primo quartile , chiamato anche quartile 1, è il valore maggiore del 25% dei dati statistici in un campione. In altre parole, il primo quartile rappresenta più del 25% dei dati osservati.

Il primo quartile è espresso dal simbolo Q ₁ e viene utilizzato per denotare i valori di dati più piccoli nel campione.

secondo quartile

Il secondo quartile , chiamato anche quartile 2, è il valore maggiore del 50% dei dati statistici in un campione. Pertanto, il secondo quartile separa il set di dati in due metà e coincide con la mediana e il quinto decile.

Il simbolo del secondo quartile è _Q2 .

terzo quartile

Il terzo quartile , chiamato anche 3° quartile, è il valore che supera il 75% dei dati statistici in un campione. In altre parole, il terzo quartile rappresenta oltre il 75% dei dati raccolti.

Il terzo quartile è espresso dal simbolo Q ₃ e rappresenta i valori più grandi nel campione.

Come calcolare i quartili

Per calcolare la posizione dei quartili di un set di dati statistici, è necessario moltiplicare il numero di quartili per la somma del numero totale di dati più uno e dividere il risultato per quattro.

La formula per i quartili è quindi la seguente:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Nota: questa formula ci dice la posizione del quartile, non il valore del quartile. Il quartile saranno i dati situati nella posizione ottenuta dalla formula.

Tuttavia, a volte il risultato di questa formula ci darà un numero decimale. Dobbiamo quindi distinguere due casi a seconda che il risultato sia un numero decimale oppure no:

Se il risultato della formula è un numero senza parte decimale , il quartile è il dato che si trova nella posizione fornita dalla formula precedente.
Se il risultato della formula è un numero con una parte decimale , il valore quartile viene calcolato utilizzando la seguente formula:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Dove x _i e x _i+1 sono i numeri delle posizioni tra le quali si trova il numero ottenuto dalla prima formula, e d è la parte decimale del numero ottenuto dalla prima formula.

Ora, forse calcolare i quartili è molto complicato per te, perché ci sono molte cose da tenere in considerazione. Ma con i due esempi nella prossima sezione, vedrai come in realtà sia abbastanza semplice.

Nota : nella comunità scientifica non c’è consenso su come calcolare i quartili, quindi puoi trovare un libro di statistica che lo spiega in modo leggermente diverso.

Esempi di calcolo dei quartili

Per comprendere appieno come vengono calcolati i quartili, di seguito troverai due esercizi svolti. Nella prima i quartili sono numeri interi e nella seconda i quartili sono numeri decimali, quindi puoi vedere quali due casi puoi trovare.

Esempio 1

Calcolare i tre quartili del seguente set di dati:

Come abbiamo visto sopra, la formula per determinare i quartili è:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

In questo caso n , il numero totale di osservazioni è 15, dobbiamo quindi sostituire n con 15 e k con 1 per trovare il primo quartile:

$\cfrac{1\cdot (15+1)}{4}=4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_1=39$

Pertanto, il primo quartile è il numero nella posizione quattro dell’elenco ordinato di valori, che in questo caso è 39.

Allo stesso modo calcoliamo il secondo quartile sostituendo il coefficiente k con a 2:

$\cfrac{2\cdot (15+1)}{4}=8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_2=48$

Il quartile 2 è quindi l’ottavo numero dell’elenco ordinato, che corrisponde al valore 48.

Infine, applichiamo la formula un’ultima volta con k = 3 per calcolare il terzo quartile:

$\cfrac{3\cdot (15+1)}{4}=12 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_3=60$

Il quartile 3 corrisponde al dato in dodicesima posizione, cioè 60.

Esempio 2

Trova i tre quartili delle seguenti serie di dati:

In questo secondo esempio abbiamo 24 osservazioni, quindi i numeri ottenuti dalla formula quartile saranno decimali.

Per prima cosa calcoliamo la posizione del primo quartile sostituendo k con 1 nella formula generale:

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (24+1)}{4}=6,25$

Ma abbiamo ottenuto il numero decimale 6,25, quindi il primo quartile si trova tra il sesto e il settimo dato, che sono rispettivamente 22 e 25. Pertanto, per calcolare il quartile esatto dobbiamo applicare la seguente formula:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

In questo caso x _i è 22, x _i+1 25 e d è la parte decimale del numero ottenuto, cioè 0,25. Ancora:

$Q_1=22+0,25\cdot (25-22)=22,75$

Ora eseguiamo la stessa procedura per trovare il secondo quartile:

$\cfrac{2\cdot (24+1)}{4}=12,5$

Anche in questo caso otteniamo un numero decimale dalla formula, in questo caso è 12,5. Dobbiamo quindi utilizzare la stessa formula con il dodicesimo e il tredicesimo numero della tabella dati, che corrisponde a 49 e 50:

$Q_2=49+0,5\cdot (50-49)=49,5$

Infine ripetiamo lo stesso procedimento per ottenere il terzo quartile:

$\cfrac{3\cdot (24+1)}{4}=18,75$

Ma il numero 18,75 è compreso tra i numeri 18 e 19, quindi il terzo quartile sarà compreso tra i valori di queste posizioni (71 e 73). Più precisamente questo sarà il valore che otterremo dalla seguente espressione:

$Q_3=71+0,75\cdot (73-71)=72,5$

calcolatore del quartile

Inserisci un set di dati statistici nella calcolatrice qui sotto per calcolare i quartili. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Quartili nei dati raggruppati

Per calcolare i quartili quando i dati vengono raggruppati in intervalli, dobbiamo prima trovare l’intervallo o il contenitore in cui rientra il quartile utilizzando la seguente formula:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Il quartile si troverà quindi nell’intervallo la cui frequenza cumulativa assoluta è immediatamente maggiore del numero ottenuto con l’espressione precedente.

E una volta conosciuto l’intervallo a cui appartiene il quartile, dobbiamo applicare la seguente formula per trovare il valore esatto del quartile:

$Q_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3$

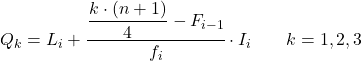
Oro:

L _i è il limite inferiore dell’intervallo in cui si trova il quartile.
n è il numero totale di osservazioni.
F _i-1 è la frequenza assoluta cumulativa dell’intervallo precedente.
f _i è la frequenza assoluta dell’intervallo in cui si trova il quartile.
I _i è la larghezza dell’intervallo quartile.

Ad esempio, ecco un esercizio per calcolare i quartili in una serie di dati raggruppati:

Per calcolare il primo quartile è necessario innanzitutto determinare l’intervallo in cui rientra. Per fare ciò applichiamo la seguente formula:

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (30+1)}{4} =7,75 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [50,60)$

Quindi il primo quartile sarà nell’intervallo la cui frequenza assoluta cumulativa è immediatamente maggiore di 7,75, in questo caso è l’intervallo [50,60) la cui frequenza assoluta cumulativa è 15. E una volta noto l’intervallo quartile, utilizziamo la seconda formula di processo :

$Q_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i$

$Q_1=50+\cfrac{\displaystyle\frac{1\cdot (30+1)}{4}-7}{8}\cdot 10=50,94$

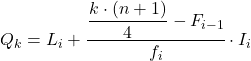
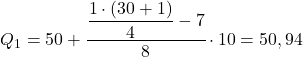
Applichiamo nuovamente la stessa procedura per ottenere il secondo quartile. Per prima cosa determiniamo l’intervallo in cui si trova il quartile:

$\cfrac{2\cdot (30+1)}{4} =15,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

L’intervallo la cui frequenza assoluta cumulativa è immediatamente maggiore di 15,5 è [60,70), con una frequenza assoluta cumulativa pari a 26. Il secondo quartile è quindi:

$Q_2=60+\cfrac{\displaystyle\frac{2\cdot (30+1)}{4}-15}{11}\cdot 10=60,45$

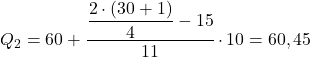
E infine, ripetiamo il processo per trovare il terzo quartile. Per prima cosa calcoliamo l’intervallo che contiene il quartile:

$\cfrac{3\cdot (30+1)}{4} =22,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

La frequenza assoluta cumulativa immediatamente superiore a 23,25 è 26, quindi l’intervallo del terzo quartile è [60,70). Applichiamo quindi la formula per calcolare il quartile con questo intervallo:

$Q_3=60+\cfrac{\displaystyle\frac{3\cdot (30+1)}{4}-15}{11}\cdot 10=67,5$

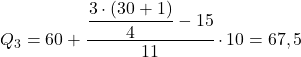
A cosa servono i quartili?

I quartili sono una misura di posizione, quindi vengono utilizzati per sapere come sono posizionati i dati. In altre parole, i valori dei tre quartili ci permettono di sapere se un dato casuale nel campione è molto grande, molto piccolo o se si tratta di un valore medio.

Se prendiamo a caso un dato dal campione, possiamo dire se il suo valore è alto o basso confrontandolo con i quartili. Se il valore dei dati casuali è inferiore al primo quartile, sarà un valore piccolo, ma se è maggiore del terzo quartile, sarà un valore grande. Allo stesso modo, se il valore di tali dati è compreso tra il primo e il terzo quartile, si tratta di un valore intermedio.

D’altra parte, i quartili vengono utilizzati anche per calcolare altre misure statistiche, come l’intervallo interquartile (o intervallo interquartile), e per creare diagrammi, come il box and whisker plot (o boxplot).

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più

Cosa sono i quartili?

primo quartile

secondo quartile

terzo quartile

Come calcolare i quartili

Esempi di calcolo dei quartili

Esempio 1

Esempio 2

calcolatore del quartile

Quartili nei dati raggruppati

A cosa servono i quartili?

Informazioni sull'autore

Benjamin anderson

Aggiungi un commento