Come calcolare i quartili per i dati raggruppati

I quartili sono valori che dividono un set di dati in quattro parti uguali.

È possibile utilizzare la seguente formula per calcolare i quartili per i dati raggruppati:

Q _i = L + (C/F) * (iN/4 – M)

Oro:

• L : Il limite inferiore dell’intervallo che contiene l’ ^iesimo quartile
• C : La larghezza della classe
• F : La frequenza dell’intervallo che contiene l’ ^iesimo quartile
• N : La frequenza totale
• M : La frequenza cumulativa che porta all’intervallo che contiene l’i- ^esimo quartile

L’esempio seguente mostra come utilizzare questa formula nella pratica.

Esempio: calcolare i quartili per i dati raggruppati

Supponiamo di avere la seguente distribuzione di frequenza:

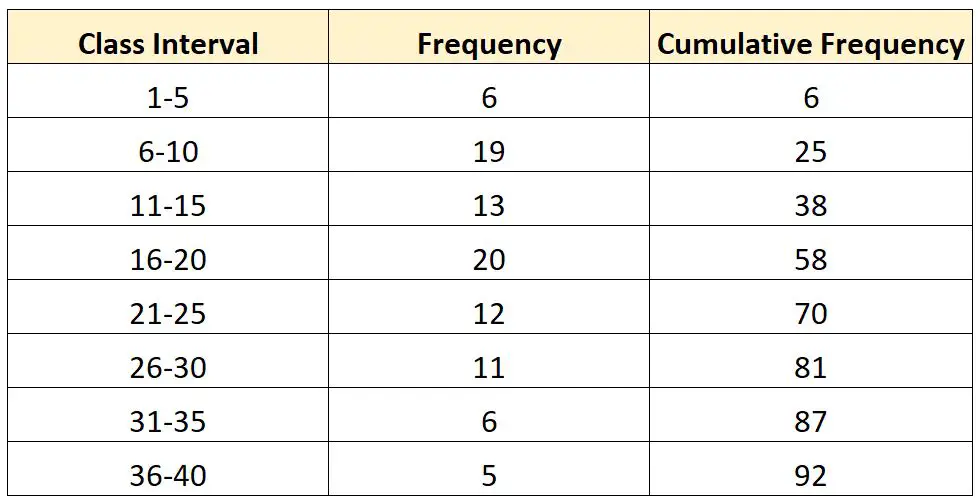
Supponiamo ora di voler calcolare il valore al terzo quartile (Q ₃ ) di questa distribuzione.

Il valore nel terzo quartile si troverà nella posizione (iN/4) nella distribuzione.

Quindi, (iN/4) = (3*92/4) = 69.

L’intervallo che contiene il terzo quartile sarà l’intervallo 21-25 poiché 69 si trova tra le frequenze cumulative di 58 e 70.

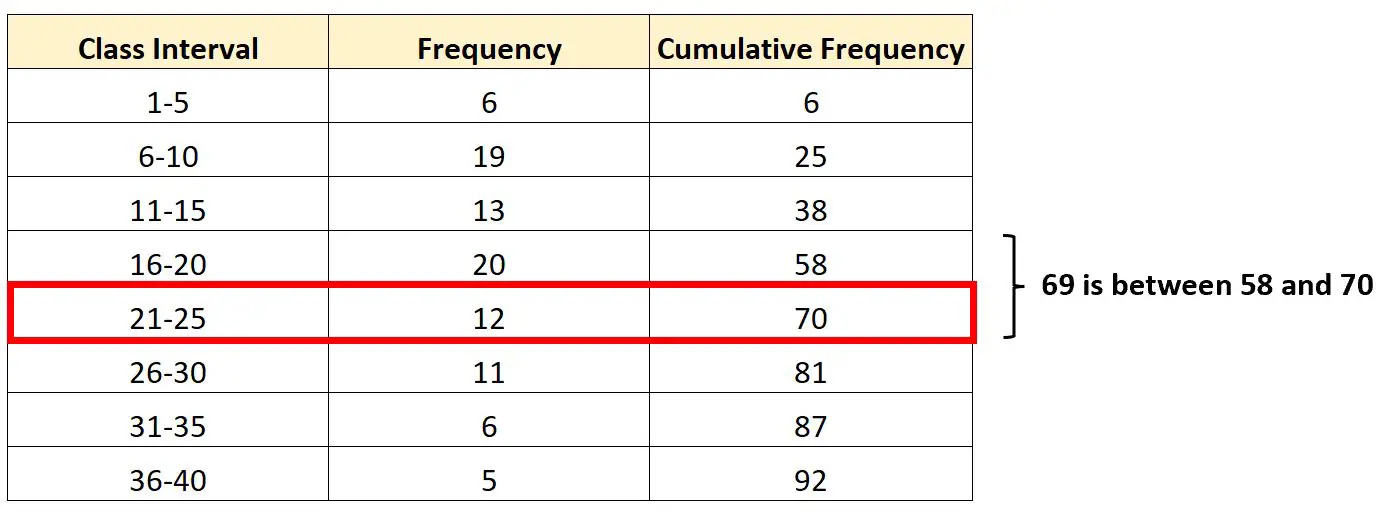
Sapendo questo, possiamo trovare ciascuno dei valori necessari da inserire nella nostra formula:

L : Il limite inferiore dell’intervallo che contiene l’ ^iesimo quartile

• Il limite inferiore dell’intervallo è 21 .

C : La larghezza della classe

• La larghezza della classe è calcolata come segue: 25 – 21 = 4 .

F : La frequenza dell’intervallo che contiene l’ ^iesimo quartile

• La frequenza della classe 21-25 è 12

N : La frequenza totale

• La frequenza cumulativa totale nella tabella è 92 .

M : La frequenza cumulativa che porta all’intervallo che contiene l’i- ^esimo quartile

• La frequenza cumulativa fino alle classi 21-25 è 58 .

Possiamo quindi inserire tutti questi valori nella formula precedente per trovare il valore nel terzo quartile:

• Q _i = L + (C/F) * (iN/4 – M)
• Q ₃ = 21 + (4/12) * ((3)(92)/4 – 58)
• _Q3 = 24,67

Il valore nel terzo quartile è 24,67 .

È possibile utilizzare un approccio simile per calcolare i valori del primo e del secondo quartile.

Risorse addizionali

Le seguenti esercitazioni forniscono ulteriori informazioni sull’utilizzo dei dati raggruppati:

Come trovare la media e la deviazione standard dei dati raggruppati
Come trovare la modalità dati raggruppati
Come trovare la mediana dei dati raggruppati
Distribuzioni di frequenza raggruppate o non raggruppate