Quasivarianza

Di Benjamin anderson Agosto 3, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la quasivarianza nelle statistiche. Scoprirai così come calcolare la quasivarianza, un esercizio risolto e quali sono le differenze tra quasivarianza e varianza. Inoltre, puoi calcolare la quasivarianza di qualsiasi set di dati con un calcolatore online.

Cos’è la quasivarianza?

In statistica, la quasivarianza è una misura di dispersione che indica la variabilità di un campione. Più precisamente, la quasivarianza è pari alla somma dei quadrati delle deviazioni divisa per il numero totale di osservazioni meno uno.

Il simbolo della quasivarianza è

$\sigma_{n-1}^2$

$s_{n-1}^2$

. a volte anche se viene utilizzato anche il simbolo

$\widehat{s}^2$

per rappresentare la quasivarianza.

La quasivarianza viene utilizzata per determinare la dispersione di un campione evitando distorsioni, motivo per cui viene spesso chiamata varianza imparziale. La quasivarianza è quindi un buon stimatore della varianza della popolazione. Infatti, quando si calcola la varianza campionaria, spesso viene utilizzata la formula della quasi-varianza al posto della formula della varianza. Di seguito entreremo nel dettaglio della differenza tra queste due misure statistiche.

Formula di quasivarianza

Per calcolare la quasivarianza, è necessario trovare la somma dei quadrati delle differenze tra i valori e la media dell’insieme di dati e successivamente dividerla per il numero totale di dati meno uno.

Quindi, la formula per calcolare la quasivarianza è la seguente:

Oro:

$\sigma_{n-1}^2$

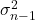
è la quasivarianza.
$x_i$

è il valore dei dati

$i$

.
$n$

è il numero totale di dati.
$\overline{X}$

è la media del set di dati.

👉 Puoi utilizzare la calcolatrice qui sotto per calcolare la quasivarianza di qualsiasi set di dati.

Forse ti starai chiedendo perché è diviso per n-1 e non per n? Bene, si tratta di eliminare il bias, in questo modo otteniamo uno stimatore imparziale. Questo è precisamente il motivo per cui la quasivarianza è un buon stimatore della varianza della popolazione.

Esempio di calcolo della quasivarianza

Ora che conosciamo la definizione di quasivarianza, risolveremo un semplice esempio in modo da poter vedere come viene calcolata la quasivarianza di una serie di dati.

Di una multinazionale conosciamo il risultato economico che ha avuto negli ultimi cinque anni, nella maggior parte ha ottenuto utili ma un anno ha presentato perdite considerevoli: 11,5,2, -9,7 milioni di euro. Calcola la quasivarianza di questo set di dati.

La prima cosa che dobbiamo fare per ottenere la quasivarianza di un insieme di dati è calcolarne la media aritmetica:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

E una volta conosciuto il valore medio dei dati, applichiamo la formula della quasivarianza:

$\sigma_{n-1}^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

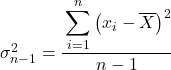
Quindi, sostituiamo i dati forniti dalle istruzioni dell’esercizio nella formula:

$\sigma_{n-1}^2=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5-1}$

Infine è sufficiente risolvere le operazioni per calcolare la quasivarianza:

$\begin{aligned}\sigma_{n-1}^2&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5-1}\\[2ex]&= \cfrac{228,8}{4} \\[2ex]&=57,2 \ \text{millones de euros}^2\end{aligned}$

Si noti che le unità della quasivarianza sono le stesse unità dei dati statistici ma al quadrato, quindi la quasivarianza di questo set di dati è 57,2 milioni ² .

➤ Vedi: Deviazione quasi standard

Calcolatore della quasivarianza

Inserisci un set di dati statistici nel seguente calcolatore per calcolarne la quasivarianza. I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Varianza e quasivarianza

Infine, vedremo la differenza tra quasivarianza e varianza, perché nonostante la somiglianza nel nome, sono anche calcolate in modo molto simile.

La differenza tra la quasivarianza e la varianza è il denominatore della formula. Per calcolare la quasivarianza è necessario dividere per n-1, tuttavia la varianza viene calcolata dividendo per n.

Pertanto, la quasivarianza e la varianza sono matematicamente correlate, poiché la quasivarianza è equivalente alla varianza moltiplicata per n (il numero totale di punti dati) e divisa per n-1.

$\sigma_{n-1}^2=\cfrac{n}{n-1}\cdot \sigma^2$

Pertanto, per lo stesso set di dati, il valore di quasivarianza sarà sempre maggiore del valore di varianza.

➤ Vedi: Proprietà delle deviazioni

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più