R vs r-square: qual è la differenza?

Due termini che gli studenti spesso confondono in statistica sono R e R al quadrato , spesso scritti ^R2 .

Nel contesto di una regressione lineare semplice :

• R: La correlazione tra la variabile predittore, x, e la variabile di risposta, y.
• R ² : Proporzione della varianza nella variabile di risposta che può essere spiegata dalla variabile predittrice nel modello di regressione.

E nel contesto di una regressione lineare multipla :

• A: La correlazione tra i valori osservati della variabile di risposta e i valori previsti della variabile di risposta realizzati dal modello.
• R ² : Proporzione della varianza della variabile di risposta che può essere spiegata dalle variabili predittive del modello di regressione.

Si noti che il valore di R ² è compreso tra 0 e 1. Quanto più il valore è vicino a 1, tanto più forte è la relazione tra le variabili predittive e la variabile di risposta.

Gli esempi seguenti mostrano come interpretare i valori R e R quadrato nei modelli di regressione lineare semplice e di regressione lineare multipla.

Esempio 1: regressione lineare semplice

Supponiamo di avere il seguente set di dati che mostra le ore studiate e i punteggi degli esami ottenuti da 12 studenti in un determinato corso di matematica:

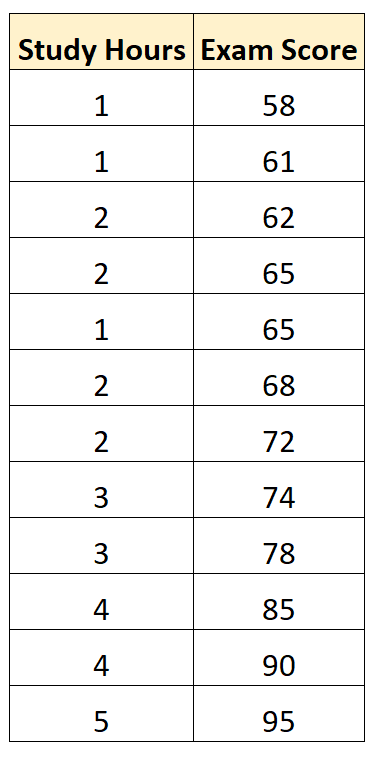
Utilizzando software statistico (come Excel, R, Python, SPSS, ecc.), possiamo adattare un semplice modello di regressione lineare utilizzando le “ore di studio” come variabile predittrice e il “voto dell’esame” come variabile di risposta .

Possiamo trovare il seguente output per questo modello:

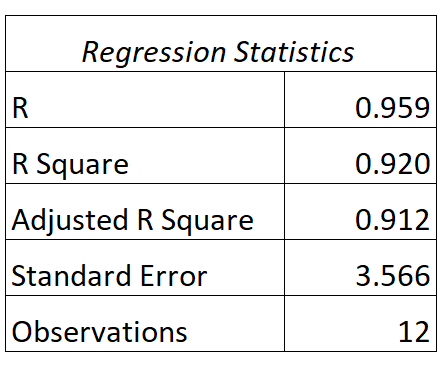
Ecco come interpretare i valori R e R al quadrato di questo modello:

• R: La correlazione tra le ore studiate e il punteggio dell’esame è 0,959 .
• R ² : L’R quadrato per questo modello di regressione è 0,920 . Questo ci dice che il 92,0% della variazione dei punteggi degli esami può essere spiegato dal numero di ore studiate.

Si noti inoltre che il valore R ² è semplicemente uguale al valore R, al quadrato:

^R2 = R * R = 0,959 * 0,959 = 0,920

Esempio 2: Regressione lineare multipla

Supponiamo di avere il seguente set di dati che mostra le ore studiate, il voto attuale dello studente e il voto dell’esame ottenuto da 12 studenti in un determinato corso di matematica:

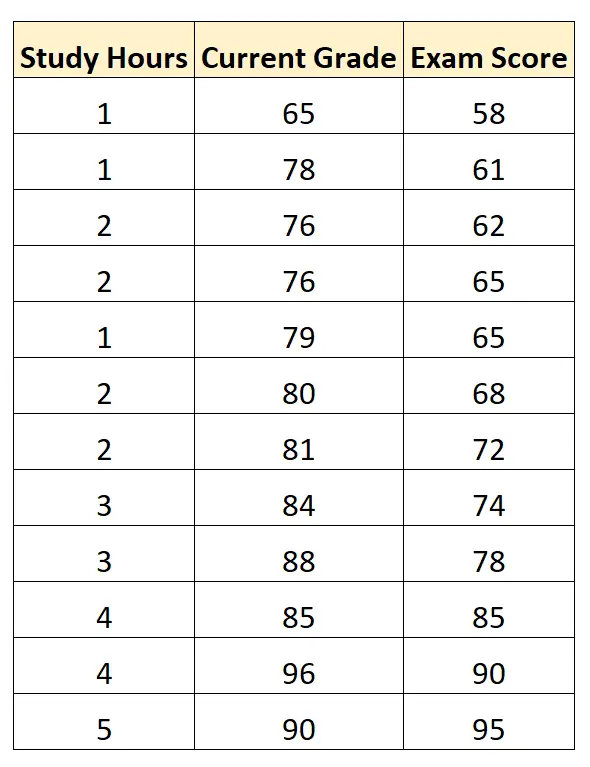
Utilizzando un software statistico, possiamo adattare un modello di regressione lineare multipla utilizzando “ore di studio” e “voto attuale” come variabili predittive e “voto di esame” come variabile di risposta.

Possiamo trovare il seguente output per questo modello:

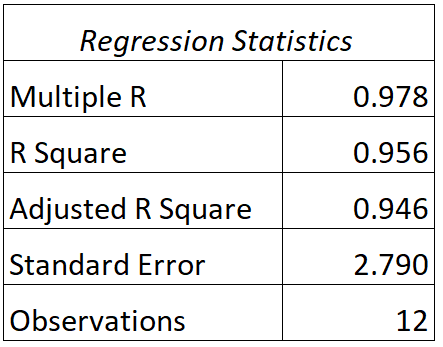
Ecco come interpretare i valori R e R al quadrato di questo modello:

• R: La correlazione tra i punteggi effettivi dei test e i punteggi dei test previsti dal modello è 0,978 .
• R ² : L’R quadrato per questo modello di regressione è 0,956 . Questo ci dice che il 95,6% della variazione dei punteggi degli esami può essere spiegata dal numero di ore studiate e dal voto attuale dello studente nella classe.

Si noti inoltre che il valore R ² è semplicemente uguale al valore R, al quadrato:

^R2 = R * R = 0,978 * 0,978 = 0,956

Risorse addizionali

Qual è un buon valore di R quadrato?
Una guida delicata alla somma dei quadrati: SST, SSR, SSE