Adattamento della curva in python (con esempi)
Spesso potresti voler adattare una curva a un set di dati in Python.

Il seguente esempio passo passo spiega come adattare le curve ai dati in Python utilizzando la funzione numpy.polyfit() e come determinare quale curva si adatta meglio ai dati.
Passaggio 1: creare e visualizzare i dati
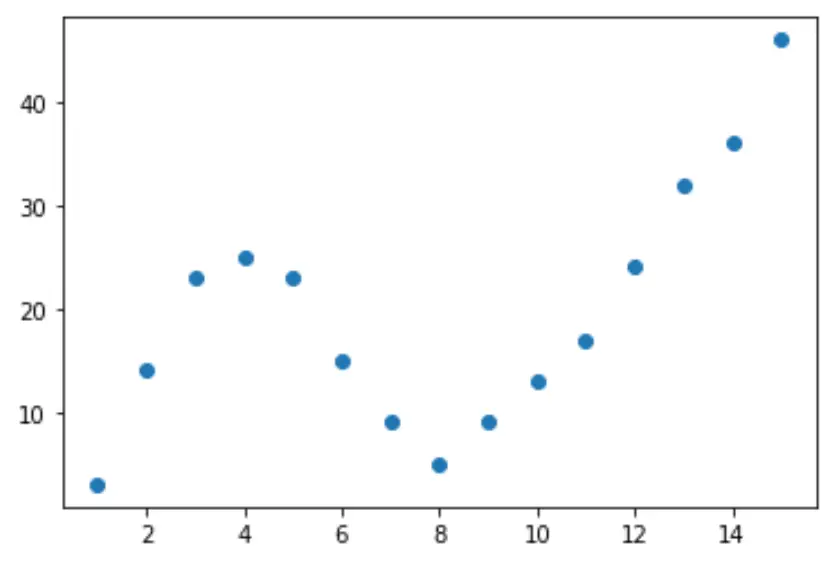
Iniziamo creando un set di dati falso, quindi creiamo un grafico a dispersione per visualizzare i dati:
import pandas as pd import matplotlib. pyplot as plt #createDataFrame df = pd. DataFrame ({' x ': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15], ' y ': [3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46]}) #create scatterplot of x vs. y plt. scatter (df. x , df. y )
Passaggio 2: regola più curve
Adattiamo quindi diversi modelli di regressione polinomiale ai dati e visualizziamo la curva di ciascun modello nello stesso grafico:
import numpy as np
#fit polynomial models up to degree 5
model1 = np. poly1d (np. polyfit (df. x , df. y , 1))
model2 = np. poly1d (np. polyfit (df. x , df. y , 2))
model3 = np. poly1d (np. polyfit (df. x , df. y , 3))
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))
model5 = np. poly1d (np. polyfit (df. x , df. y , 5))
#create scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )
#add fitted polynomial lines to scatterplot
plt. plot (polyline, model1(polyline), color=' green ')
plt. plot (polyline, model2(polyline), color=' red ')
plt. plot (polyline, model3(polyline), color=' purple ')
plt. plot (polyline, model4(polyline), color=' blue ')
plt. plot (polyline, model5(polyline), color=' orange ')
plt. show ()
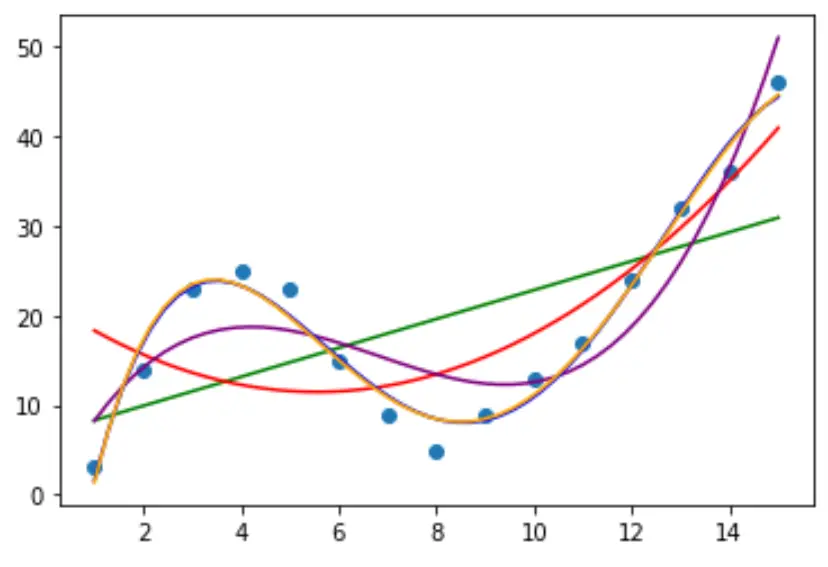
Per determinare quale curva si adatta meglio ai dati, possiamo osservare il quadrato R corretto di ciascun modello.
Questo valore indica la percentuale di variazione nella variabile di risposta che può essere spiegata dalle variabili predittive nel modello, adattata al numero di variabili predittive.
#define function to calculate adjusted r-squared def adjR(x, y, degree): results = {} coeffs = np. polyfit (x, y, degree) p = np. poly1d (coeffs) yhat = p(x) ybar = np. sum (y)/len(y) ssreg = np. sum ((yhat-ybar)**2) sstot = np. sum ((y - ybar)**2) results[' r_squared '] = 1- (((1-(ssreg/sstot))*(len(y)-1))/(len(y)-degree-1)) return results #calculated adjusted R-squared of each model adjR(df. x , df. y , 1) adjR(df. x , df. y , 2) adjR(df. x , df. y , 3) adjR(df. x , df. y , 4) adjR(df. x , df. y , 5) {'r_squared': 0.3144819} {'r_squared': 0.5186706} {'r_squared': 0.7842864} {'r_squared': 0.9590276} {'r_squared': 0.9549709}
Dal risultato, possiamo vedere che il modello con l’R quadrato corretto più alto è il polinomio di quarto grado, che ha un R quadrato corretto di 0,959 .
Passaggio 3: Visualizza la curva finale
Infine, possiamo creare un grafico a dispersione con la curva del modello polinomiale di quarto grado:
#fit fourth-degree polynomial model4 = np. poly1d (np. polyfit (df. x , df. y , 4)) #define scatterplot polyline = np. linspace (1, 15, 50) plt. scatter (df. x , df. y ) #add fitted polynomial curve to scatterplot plt. plot (polyline, model4(polyline), ' -- ', color=' red ') plt. show ()

Possiamo anche ottenere l’equazione per questa riga utilizzando la funzione print() :
print (model4)
4 3 2
-0.01924x + 0.7081x - 8.365x + 35.82x - 26.52
L’equazione della curva è la seguente:
y = -0,01924x 4 + 0,7081x 3 – 8,365x 2 + 35,82x – 26,52
Possiamo utilizzare questa equazione per prevedere il valore della variabile di risposta in base alle variabili predittive nel modello. Ad esempio, se x = 4, allora dovremmo prevedere che y = 23,32 :
y = -0,0192(4) 4 + 0,7081(4) 3 – 8,365(4) 2 + 35,82(4) – 26,52 = 23,32
Risorse addizionali
Un’introduzione alla regressione polinomiale
Come eseguire la regressione polinomiale in Python