Come calcolare i rapporti di probabilità in sas (con esempio)

In statistica, un odds ratio ci dice il rapporto tra le probabilità che un evento si verifichi in un gruppo di trattamento e le probabilità che un evento si verifichi in un gruppo di controllo.

Spesso calcoliamo un rapporto probabilità quando eseguiamo l’analisi su una tabella 2 per 2, che assume il seguente formato:

Per calcolare un rapporto odd in SAS, possiamo utilizzare l’istruzione PROC FREQ .

L’esempio seguente mostra come utilizzare questa affermazione nella pratica.

Esempio: calcolo di un odds ratio in SAS

Diciamo che 50 giocatori di basket utilizzano un nuovo programma di allenamento e 50 giocatori utilizzano un vecchio programma di allenamento. Alla fine del programma, testiamo ogni giocatore per vedere se supera un determinato test di abilità.

La tabella seguente mostra il numero di giocatori che hanno superato e fallito, in base al programma utilizzato:

Diciamo che vogliamo calcolare un rapporto probabilità per confrontare le possibilità che un giocatore superi il test di abilità utilizzando il nuovo programma rispetto a quelle che utilizzano il vecchio programma.

Possiamo utilizzare la seguente sintassi con PROC FREQ in SAS con le istruzioni chisq e relrisk per calcolare questo odds ratio insieme ai relativi valori di rischio:

 /*create dataset*/
data my_data;
    input result $program $count;
    datalines ;
Passed New 34
Passed Old 39
_Failed New 16
_Failed Old 11
;
run ;
/*calculate odds ratio*/
proc freq data =my_data;
    weightcount ;
    tables program * result / chisq relrisk ;
run ;

La prima tabella dei risultati mostra la frequenza di ciascuna combinazione di variabili categoriali:

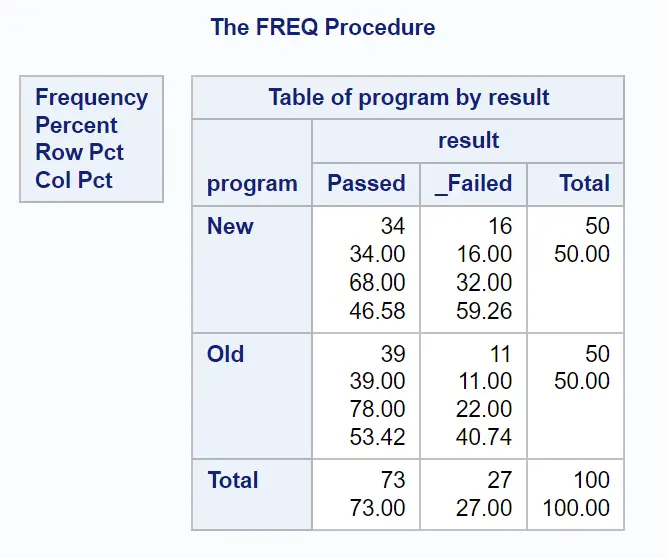
L’ultima tabella dei risultati mostra il rapporto di probabilità che ci interessa:

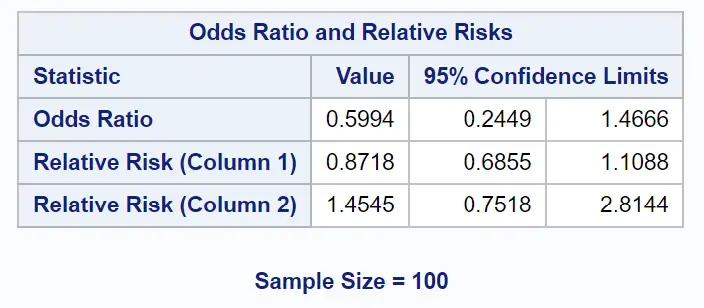
L’odds ratio risulta essere 0,5994 .

Interpretiamo questo nel senso che le probabilità che un giocatore superi il test utilizzando il nuovo programma sono solo 0,5994 volte le probabilità che un giocatore superi il test utilizzando il vecchio programma.

In altre parole, le possibilità che un giocatore superi il test vengono effettivamente ridotte di circa il 40,06% grazie all’utilizzo del nuovo programma.

Possiamo anche utilizzare i valori nelle colonne Limiti di confidenza del 95% dei risultati per costruire il seguente intervallo di confidenza del 95% per l’odds ratio:

Intervallo di confidenza al 95% per l’odds ratio: [0,2449, 1,4666] .

Siamo sicuri al 95% che il vero odds ratio tra il nuovo e il vecchio programma di allenamento sia contenuto in questo intervallo.

Poiché l’intervallo di confidenza contiene il valore del rapporto odd pari a 1, ciò significa che il rapporto odd non è statisticamente significativo.

In altre parole, sappiamo dall’odds ratio che le possibilità di successo di un giocatore utilizzando il nuovo programma sono inferiori rispetto alle possibilità di successo utilizzando il vecchio programma, ma la differenza tra queste possibilità non è in realtà statisticamente significativa.

Risorse addizionali

I seguenti tutorial forniscono ulteriori informazioni sui rapporti di probabilità:

La differenza tra odds ratio e rischio relativo
La guida completa: come segnalare i rapporti di probabilità
Come calcolare un intervallo di confidenza per un odds ratio