Recinzioni superiori e inferiori: definizione ed esempio

Nelle statistiche, i limiti superiore e inferiore rappresentano i valori di soglia per i valori anomali superiori e inferiori in un set di dati. Sono calcolati come segue:

• Chiusura inferiore = Q1 – (1,5*IQR)
• Chiusura superiore = Q3 + (1,5*IQR)

dove IQR sta per “intervallo interquartile” che rappresenta la differenza tra il 75° percentile (Q3) e il 25° percentile (Q1) in un set di dati.

Un’osservazione situata sopra la barriera superiore o sotto la barriera inferiore è spesso considerata un valore anomalo.

Esempio: Calcolo della guida superiore e inferiore

Supponiamo di avere il seguente set di dati:

 Dataset: 11, 13, 14, 14, 15, 16, 18, 22, 24, 27, 34, 36, 38, 41, 45

Possiamo utilizzare i seguenti passaggi per calcolare la recinzione superiore e inferiore del set di dati:

Passaggio 1: cerca Q1 e Q3.

Q1 rappresenta il 25° percentile del set di dati e Q3 rappresenta il 75° percentile. Secondo il calcolatore dell’intervallo interquartile, Q1 e Q3 per questo set di dati sono:

• T1: 14
• T3: 36

Passaggio 2: trova l’IQR (intervallo interquartile).

L’intervallo interquartile rappresenta la differenza tra Q3 e Q1, che viene calcolata come segue:

• Scala interquartile: Q3 – Q1 = 36 – 14 = 22

Passaggio 3: trova la recinzione superiore e inferiore

Possiamo utilizzare le seguenti formule per calcolare le recinzioni superiore e inferiore:

• Chiusura inferiore: Q1 – (1,5*IQR) = 14 – (1,5*22) = -19
• Recinzione superiore: Q3 + (1,5*IQR) = 36 + (1,5*22) = 69

Poiché nessuna delle osservazioni nel nostro set di dati cade al di sotto del limite inferiore o al di sopra del limite superiore, nessuna delle osservazioni sarebbe considerata anomala.

Possiamo anche creare un boxplot per visualizzare la nostra distribuzione dei valori dei dati nonché le barriere superiore e inferiore:

Bonus: calcolatore di chiusura superiore e inferiore

Invece di calcolare manualmente i recinti superiore e inferiore di un set di dati, sentiti libero di utilizzare il calcolatore del recinto superiore e inferiore:

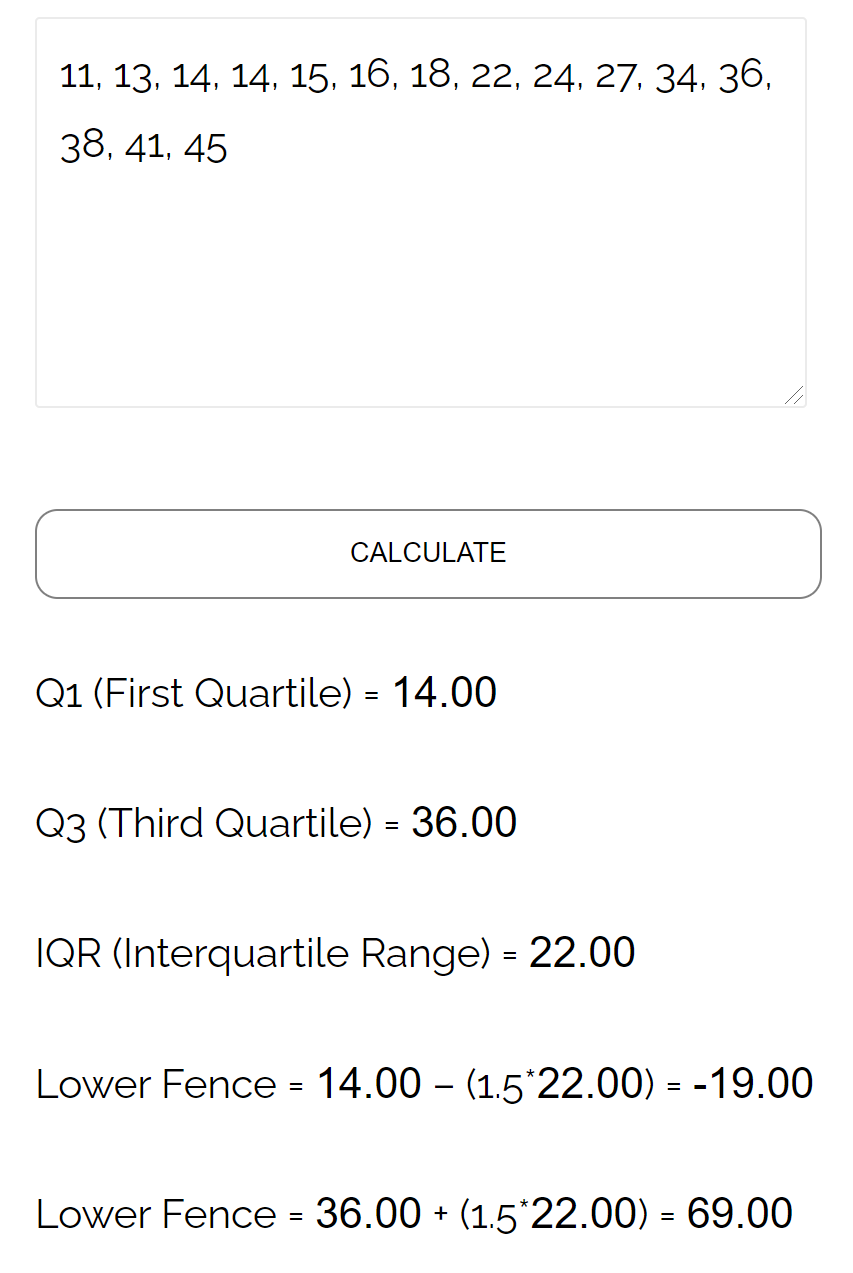
Puoi trovare calcolatori statistici più utili in questa pagina .