Regola dell'addizione (o regola dell'addizione)

Questo articolo spiega cos’è la regola dell’addizione, nota anche come regola dell’addizione, e a cosa serve in probabilità e statistica. Inoltre, potrai vedere qual è la formula per la regola dell’addizione e risolvere esercizi che mostrano come usarla.

Qual è la regola dell’addizione (o regola dell’addizione)?

La regola dell’addizione (o regola dell’addizione ) afferma che la somma delle probabilità di due eventi è uguale alla somma della probabilità che ciascun evento si verifichi separatamente meno la probabilità che entrambi gli eventi si verifichino contemporaneamente.

Pertanto, la formula per la regola dell’addizione è P(A⋃B)=P(A)+P(B)−P(A⋂B).

Pertanto, per sommare due probabilità, non possiamo semplicemente sommare ciascuna probabilità, poiché dobbiamo anche sottrarre il termine che rappresenta la probabilità congiunta dei due eventi. Tuttavia, in alcuni casi, solo sommando la probabilità di ciascun evento si può ottenere il risultato corretto della somma delle probabilità. Di seguito vedremo quali sono questi casi.

In breve, la regola dell’addizione serve per calcolare la probabilità che si verifichi un evento o un altro, cioè la probabilità che si verifichi almeno uno dei due eventi possibili.

Formula della regola di addizione

La regola dell’addizione dice che per calcolare la probabilità che si verifichi l’evento A o l’evento B, dobbiamo sommare la probabilità che si verifichi l’evento A più la probabilità che si verifichi l’evento B e sottrarre la probabilità che entrambi gli eventi si verifichino contemporaneamente. .

La formula per la regola dell’addizione (o regola dell’addizione) è quindi la seguente:

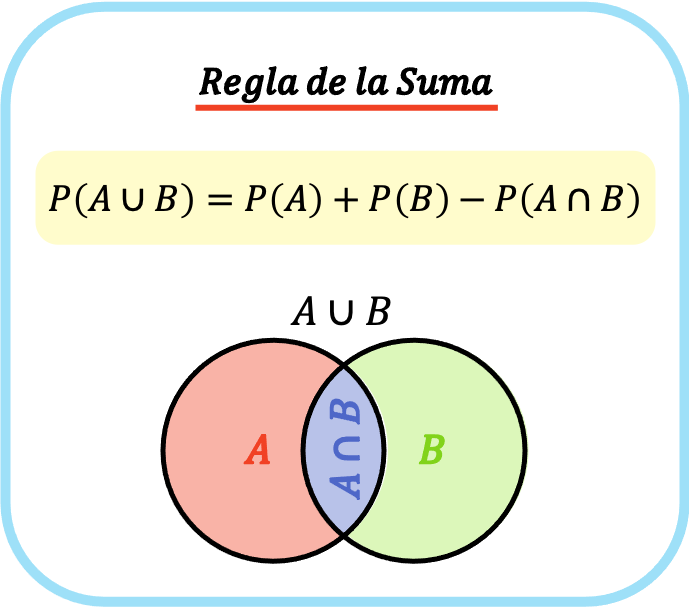
Oro:

• 

  è la probabilità dell’evento A o dell’evento B.

• 

  è la probabilità che si verifichi l’evento A.

• 

  è la probabilità che si verifichi l’evento B.

• 

  è la probabilità congiunta che si verifichino l’evento A e l’evento B.

Pertanto, per utilizzare la regola della somma, è necessario sapere come calcolare la probabilità congiunta di due eventi. Puoi vedere come è fatto nel seguente link:

Esempio di regola di somma per eventi esclusivi

Per finire di comprendere il concetto, vediamo un esempio di come applicare la regola dell’addizione.

• Mettiamo in una scatola 10 palline blu, 6 palline arancioni e 4 palline verdi. Qual è la probabilità di estrarre una pallina blu o arancione?

L’esercizio ci chiede di determinare la probabilità che si verifichi un evento o un altro. Pertanto, per risolvere il problema, dobbiamo utilizzare la formula della regola di addizione:

Quindi, per prima cosa calcoliamo la probabilità che ciascun evento si verifichi separatamente utilizzando la regola di Laplace :

Tuttavia, in questo caso, gli eventi non possono verificarsi contemporaneamente, perché sono due eventi che si escludono a vicenda . Quindi se disegniamo una pallina blu non potremo più disegnare una pallina arancione, e viceversa.

Pertanto, la probabilità congiunta di entrambi gli eventi è zero e quindi la formula della regola della somma è semplificata:

Quindi il calcolo della probabilità di prendere una pallina blu o una pallina arancione è il seguente:

In breve, la probabilità di estrarre una pallina blu o arancione dalla scatola è dell’80%.

Esempio di regola di aggiunta per eventi non esclusivi

Avendo visto un esempio concreto della regola di addizione quando gli eventi sono esclusivi, vedremo ora come viene utilizzata questa legge quando gli eventi non sono esclusivi.

• Se lanciamo una moneta due volte, qual è la probabilità che esca testa almeno al primo lancio?

In questo caso gli eventi non si escludono a vicenda, poiché possiamo ottenere “testa” al primo lancio e “croce” al secondo lancio. La formula per la regola dell’addizione non è quindi semplificata ed è la seguente:

Quindi, dobbiamo prima calcolare la probabilità di ottenere “testa” lanciando una moneta applicando la regola di Laplace:

Inoltre, i due eventi sono indipendenti, quindi possiamo calcolare la probabilità congiunta dei due eventi utilizzando la regola del prodotto :

Infine, per trovare la probabilità che esca testa in almeno uno dei due lanci, è sufficiente sostituire i valori nella formula della regola di addizione ed eseguire il calcolo:

In conclusione, la probabilità che lanciando due volte una moneta si ottenga testa almeno una volta è del 75%.