Adattamento della curva in excel (con esempi)

Spesso potresti voler trovare l’equazione che meglio si adatta a una curva per un insieme di dati in Excel.

Fortunatamente, questo è abbastanza semplice da fare utilizzando la funzione Trendline di Excel.

Questo tutorial fornisce un esempio passo passo di come adattare un’equazione a una curva in Excel.

Passaggio 1: creare i dati

Innanzitutto, creiamo un set di dati falso con cui lavorare:

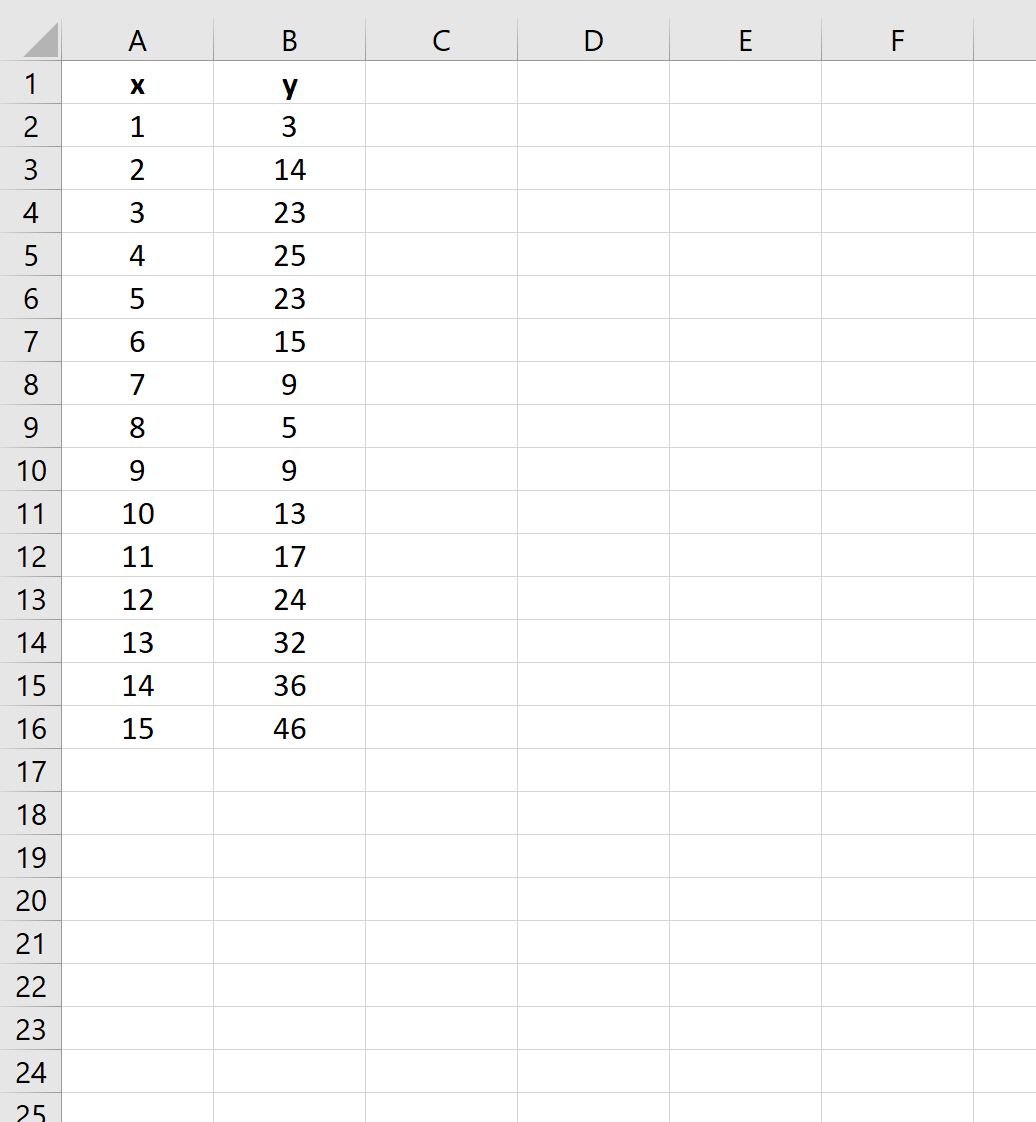
Passaggio 2: crea un grafico a dispersione

Successivamente, creiamo un grafico a dispersione per visualizzare il set di dati.

Innanzitutto, evidenzia le celle A2:B16 come segue:

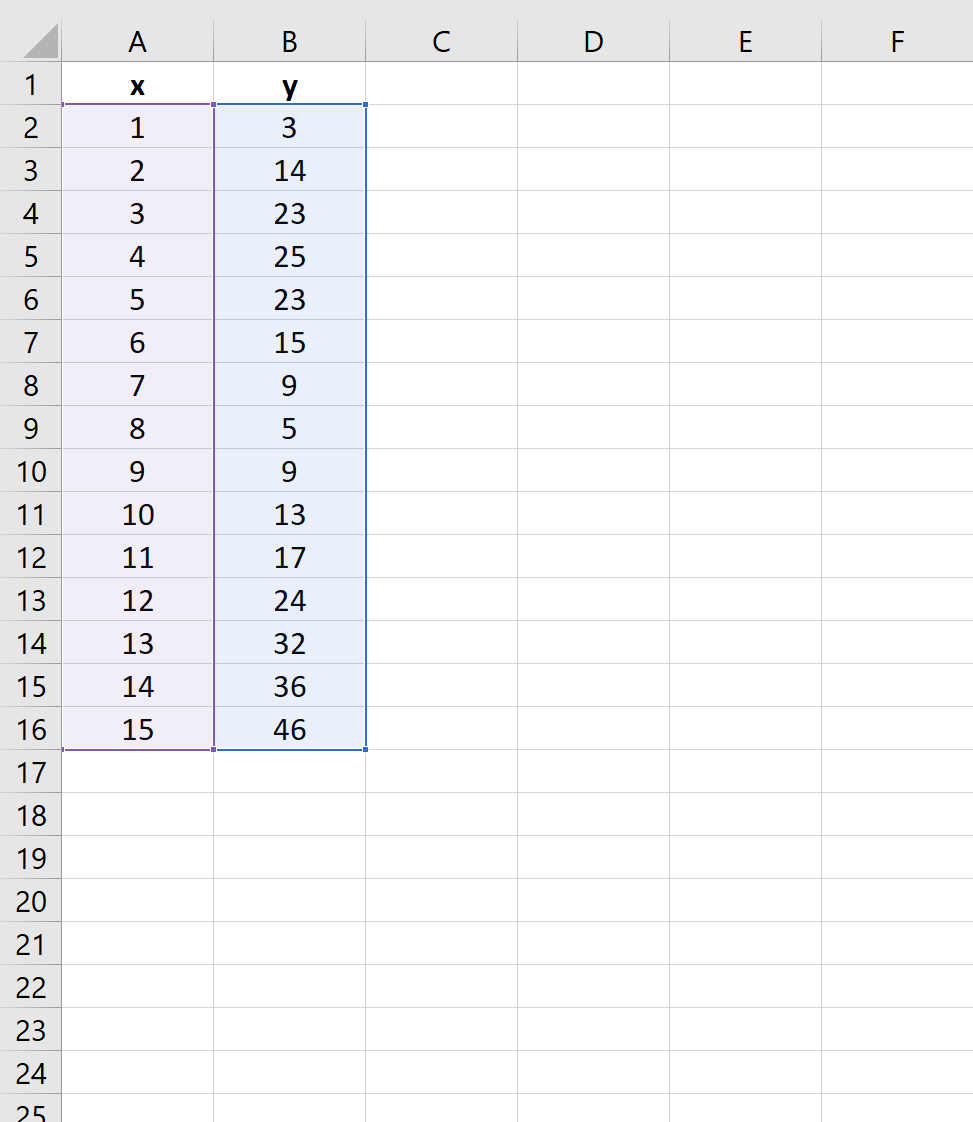
Successivamente, fai clic sulla scheda Inserisci lungo la barra multifunzione superiore, quindi fai clic sulla prima opzione di grafico in Dispersione :

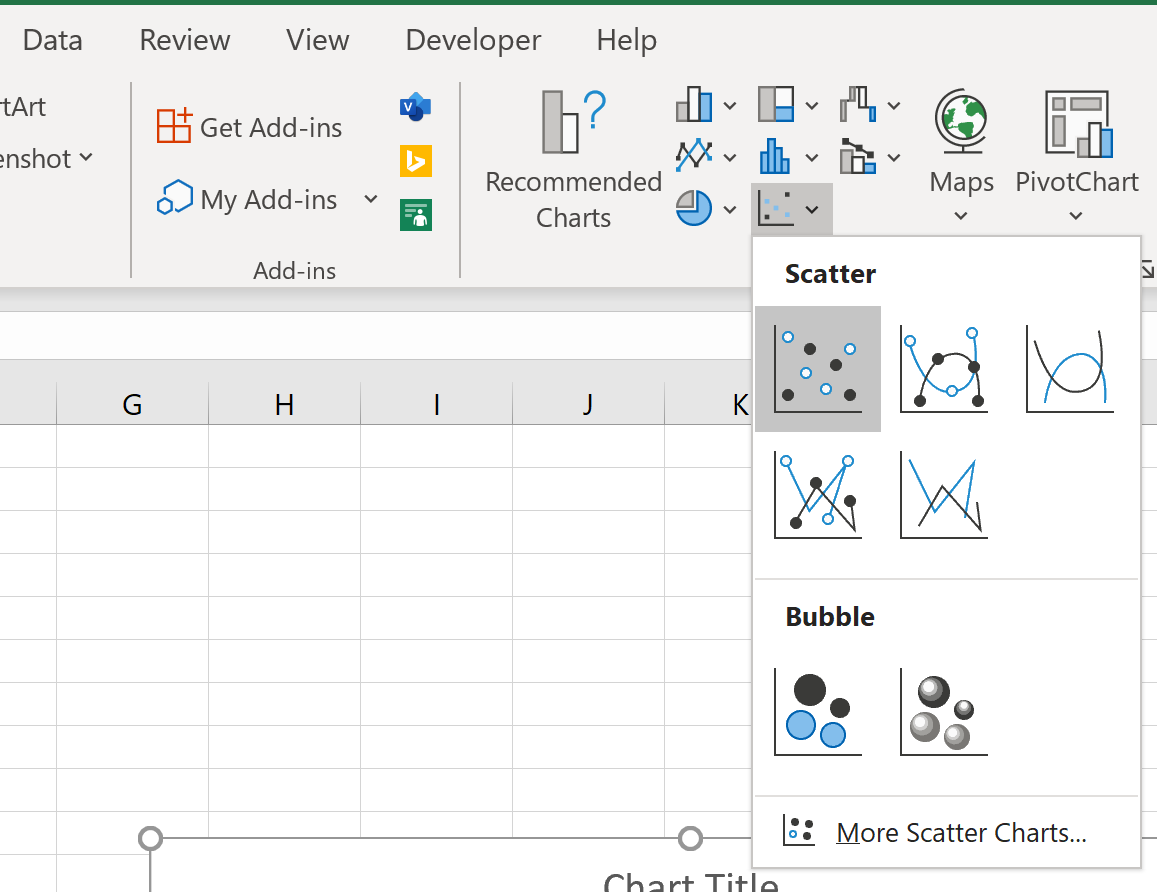
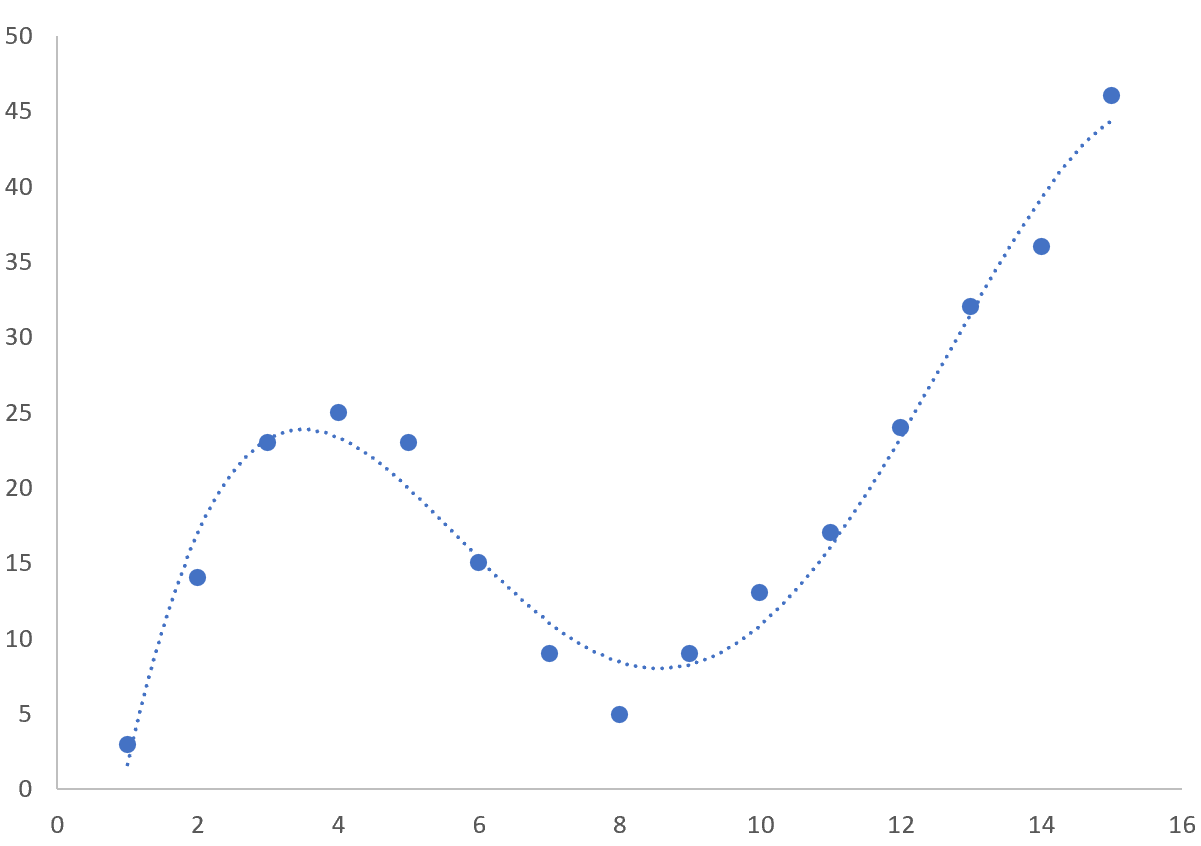
Ciò produce il seguente grafico a dispersione:

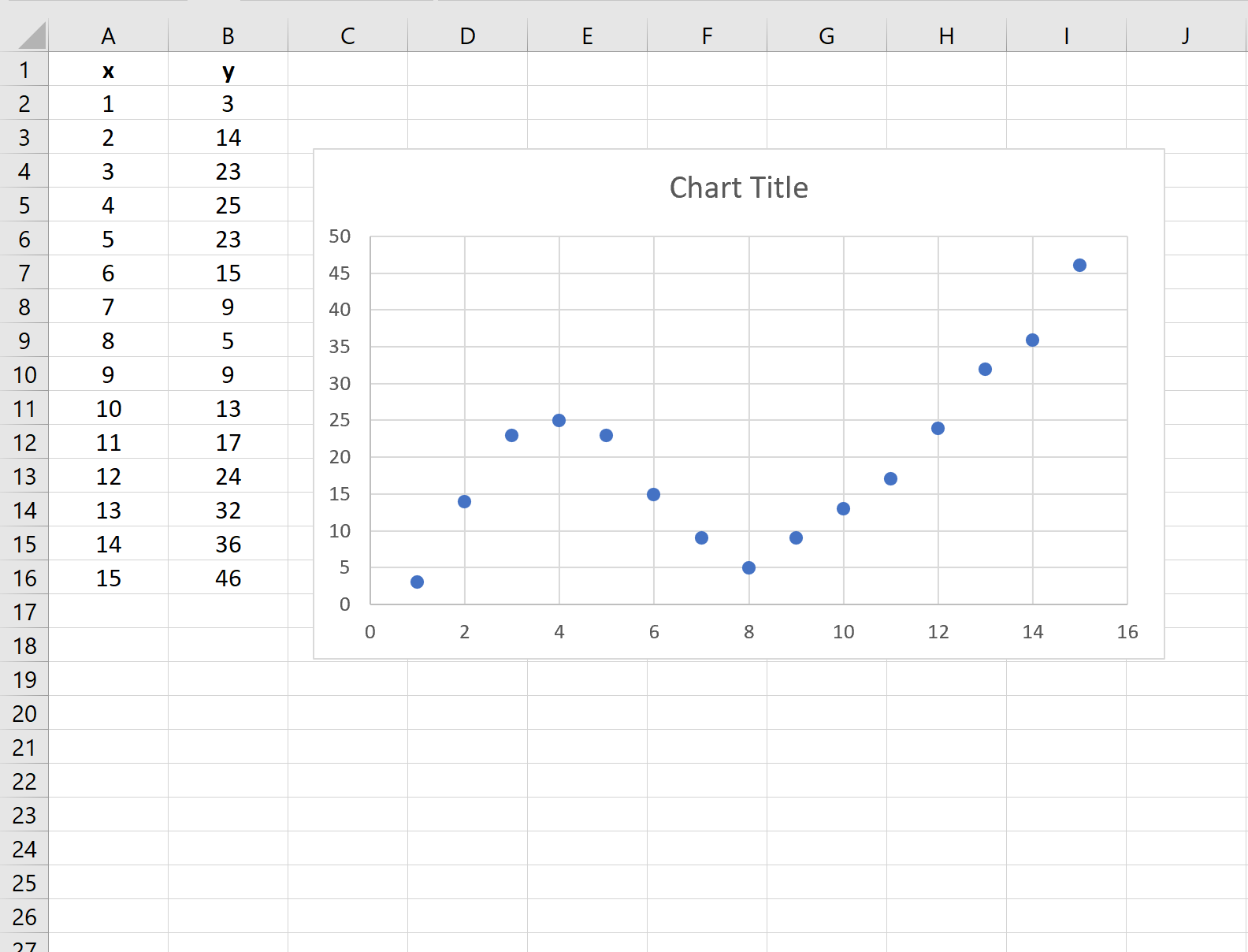
Passaggio 3: aggiungi una linea di tendenza

Successivamente, fai clic in un punto qualsiasi del grafico a dispersione. Quindi fare clic sul segno + nell’angolo in alto a destra. Nel menu a discesa, fai clic sulla freccia accanto a Trendline , quindi su Altre opzioni :

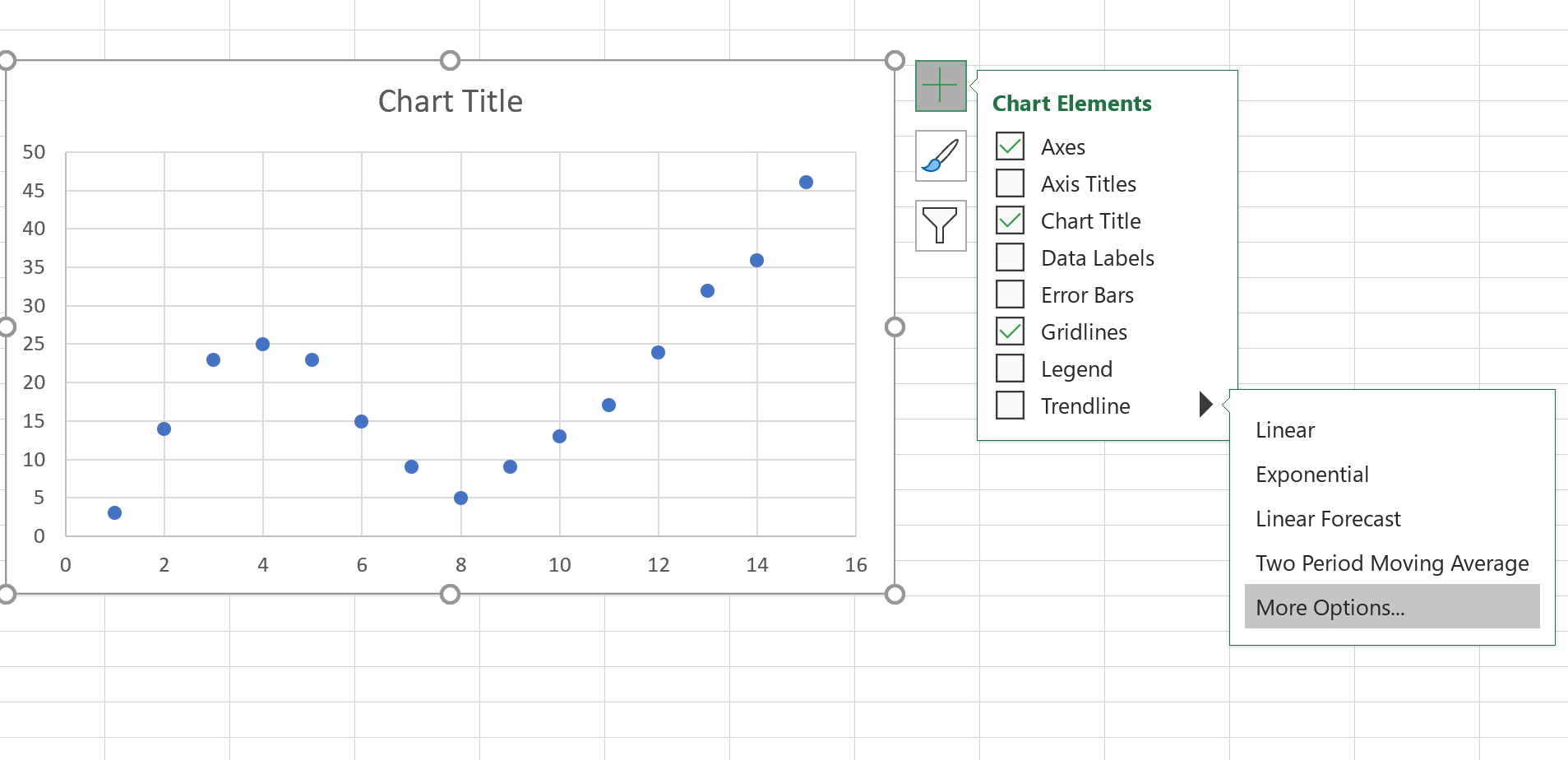
Nella finestra che appare a destra, fai clic sul pulsante accanto a Polinomio . Quindi seleziona le caselle accanto a Mostra equazione sul grafico e Mostra valore R quadrato sul grafico .

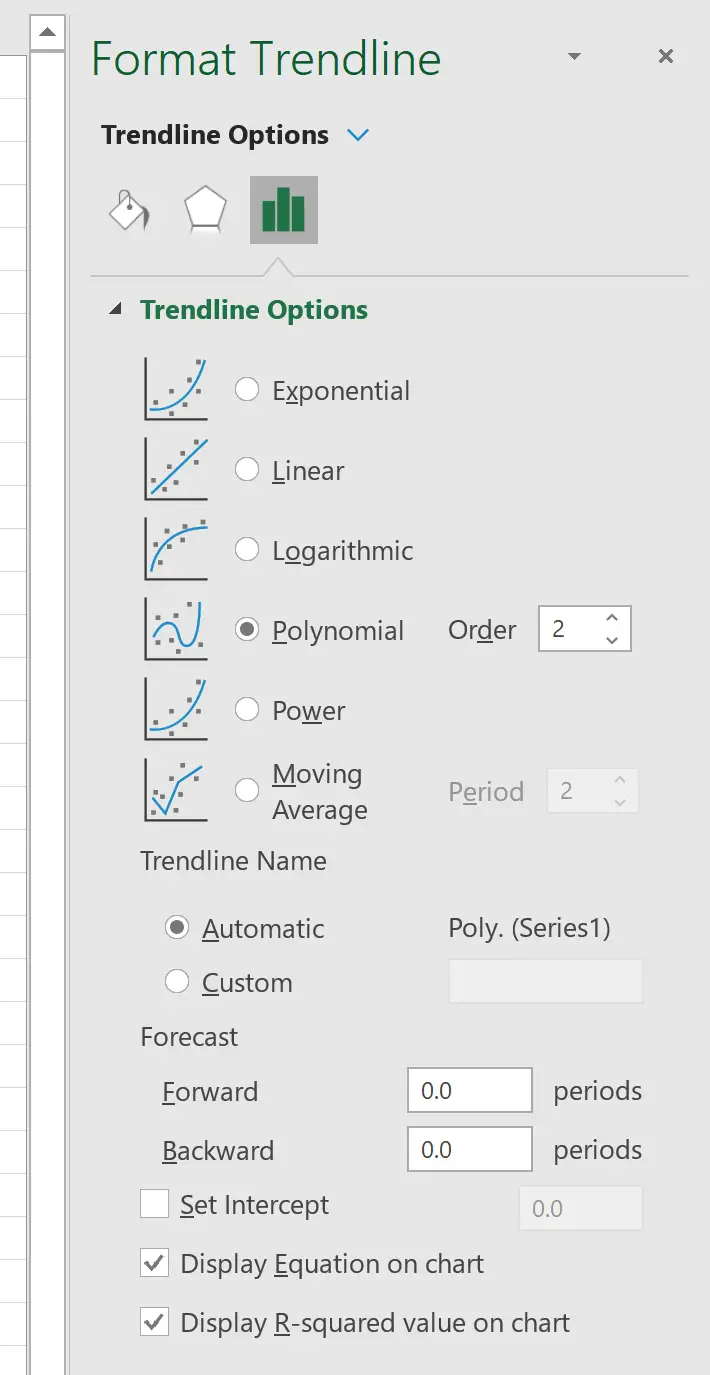
Ciò produce la seguente curva sulla nuvola di punti:

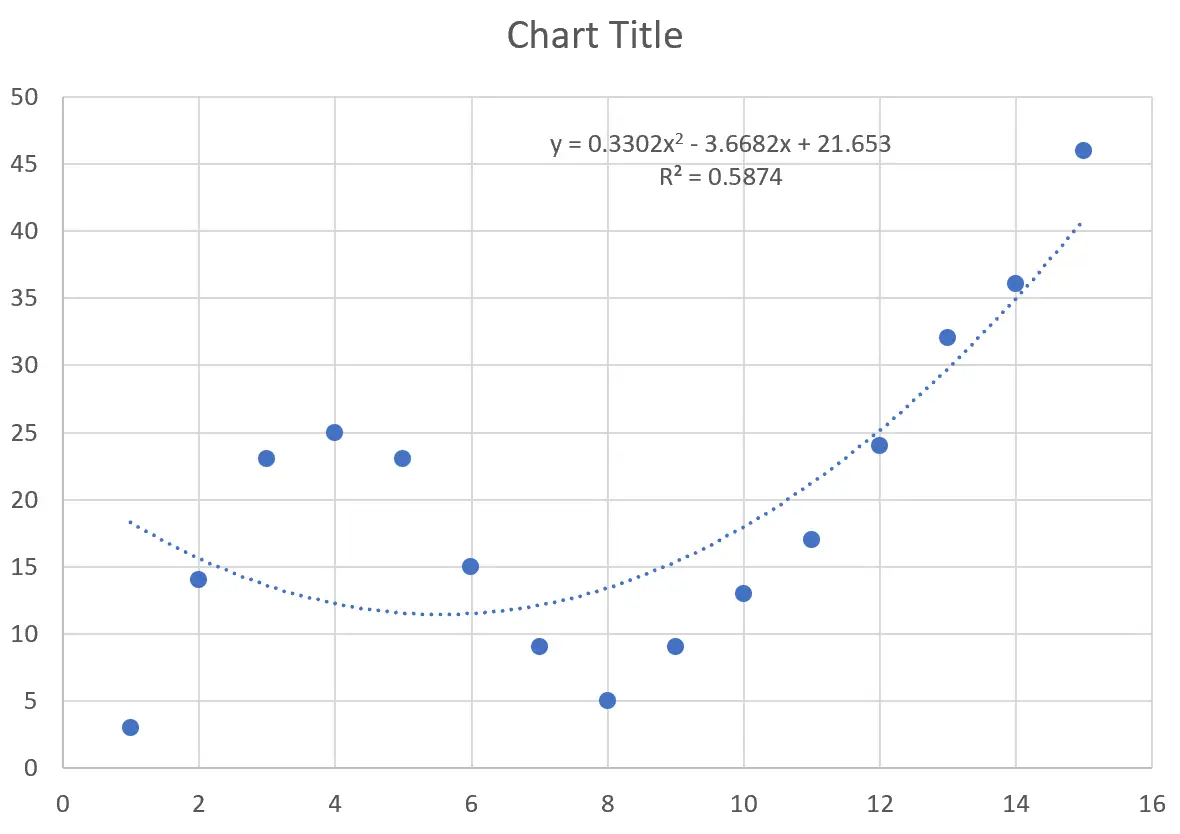
L’equazione della curva è la seguente:

y = ^0,3302×2 – 3,6682x + 21,653

L’ R quadrato ci dice la percentuale di variazione nella variabile di risposta che può essere spiegata dalle variabili predittive. La R al quadrato per questa curva particolare è 0,5874 .

Passaggio 4: scegli la migliore linea di tendenza

Possiamo anche aumentare l’ordine del polinomio che stiamo utilizzando per vedere se una curva più flessibile fornisce un adattamento migliore al set di dati.

Ad esempio, potremmo scegliere di impostare l’ordine dei polinomi su 4:

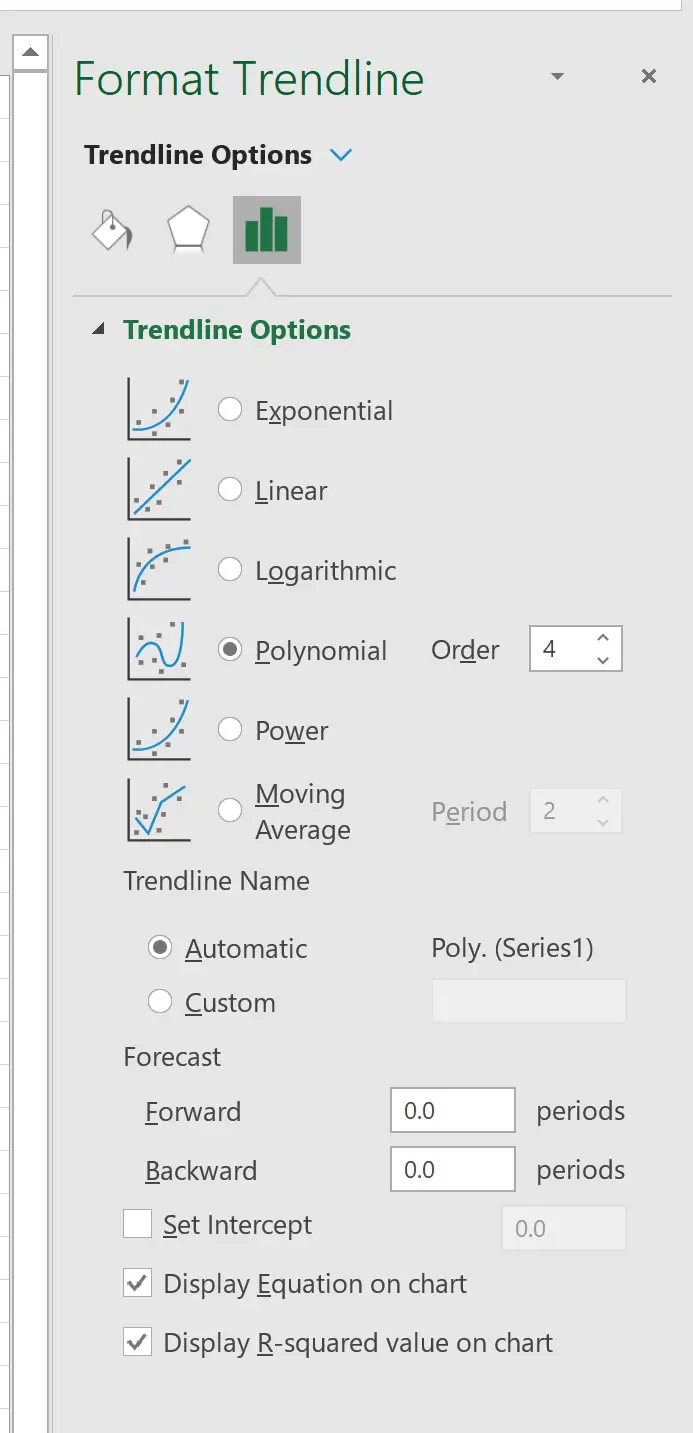
Ciò si traduce nella seguente curva:

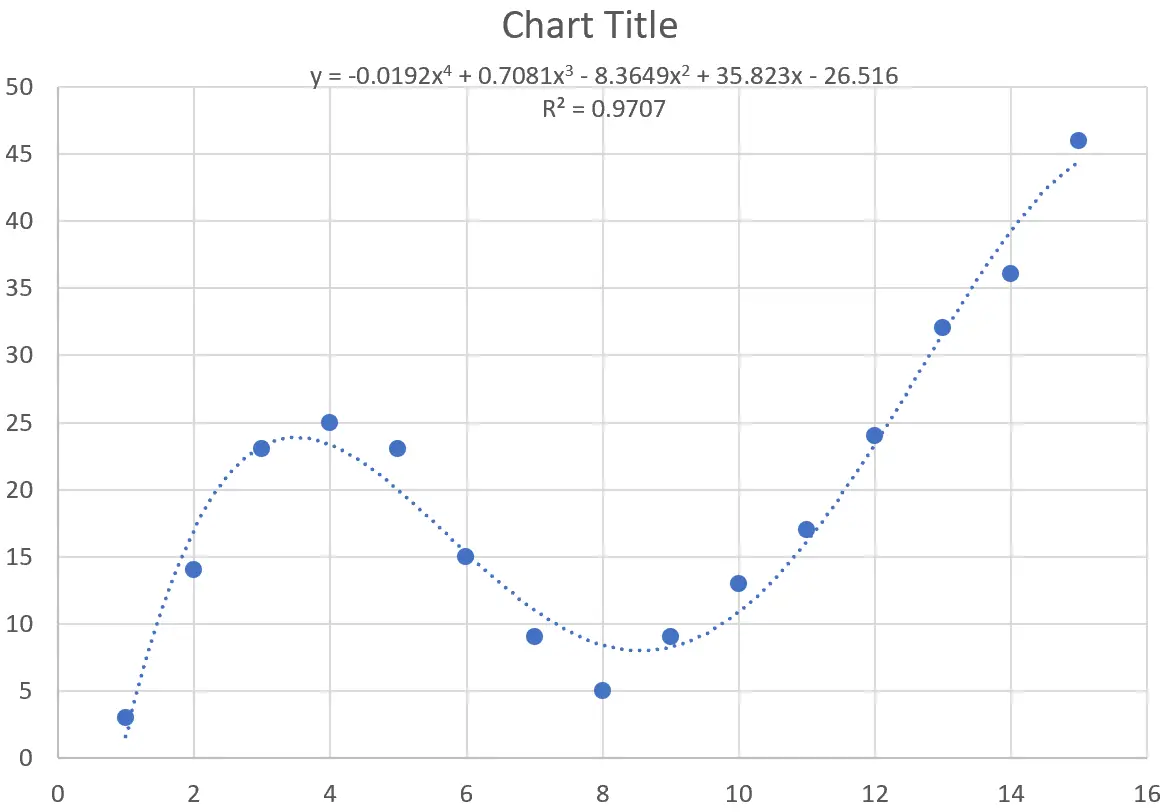
L’equazione della curva è la seguente:

y = -0,0192x ⁴ + 0,7081x ³ – 8,3649x ² + 35,823x – 26,516

La R al quadrato per questa curva particolare è 0,9707 .

Questo R quadrato è considerevolmente più alto di quello della curva precedente, indicando che corrisponde molto più da vicino al set di dati.

Possiamo anche utilizzare questa equazione della curva per prevedere il valore della variabile di risposta in base alla variabile predittrice. Ad esempio, se x = 4, allora dovremmo prevedere che y = 23,34 :

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,3649(4) ² + 35,823(4) – 26,516 = 23,34

Puoi trovare altri tutorial su Excel in questa pagina .