Come eseguire la regressione loess in r (con esempio)

La regressione LOESS , a volte chiamata regressione locale, è un metodo che utilizza l’aggiustamento locale per adattare un modello di regressione a un insieme di dati.

Il seguente esempio passo passo mostra come eseguire la regressione LOESS in R.

Passaggio 1: creare i dati

Innanzitutto, creiamo il seguente frame di dati in R:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
                 y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))

#view first six rows of data frame
head(df)

  xy
1 1 1
2 2 4
3 3 7
4 4 13
5 5 19
6 6 24

Passaggio 2: adattamento di più modelli di regressione LOESS

Possiamo utilizzare la funzione loess() per adattare più modelli di regressione LOESS a questo set di dati, utilizzando valori diversi per il parametro span :

 #fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50) 

loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75) 

loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90) 

#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
        col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')

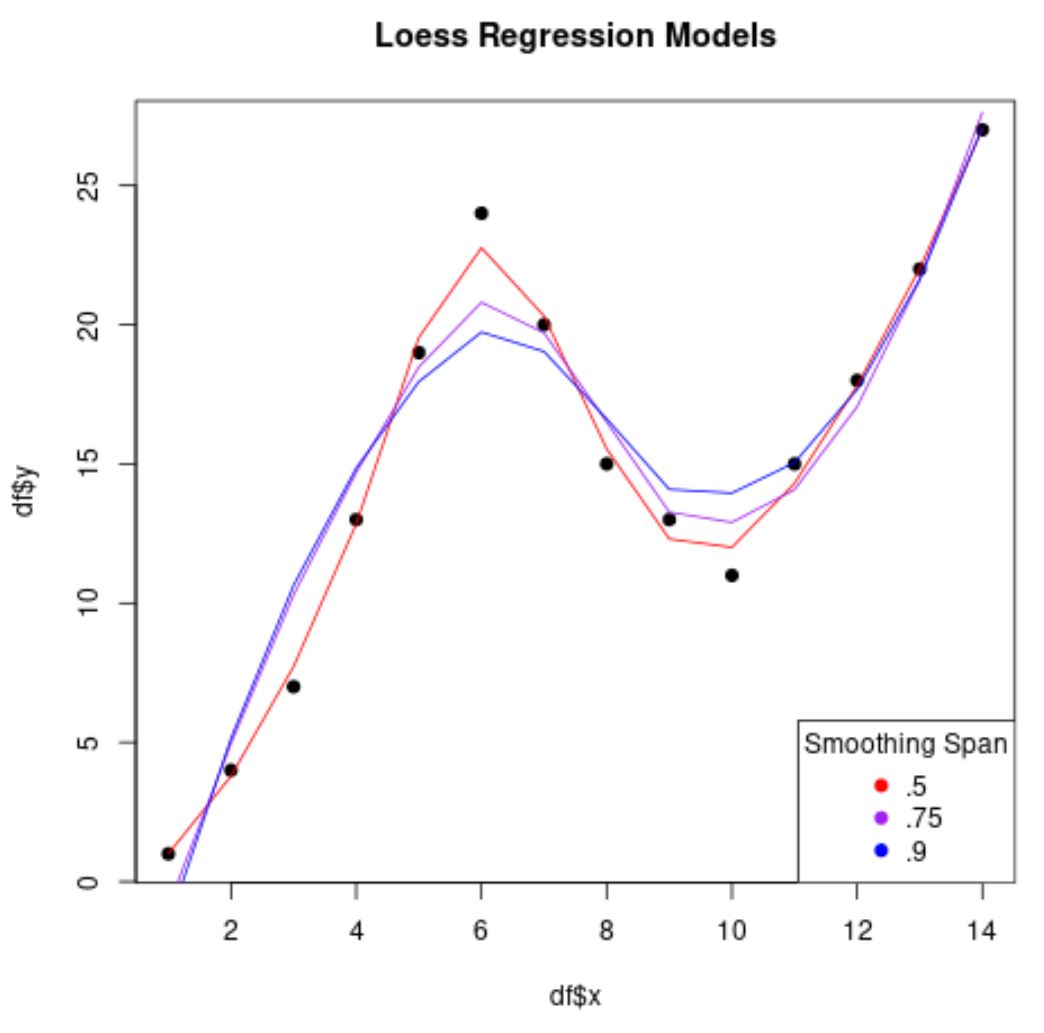
Si noti che quanto più basso è il valore utilizzato per span , tanto meno “fluido” sarà il modello di regressione e tanto più il modello tenterà di adattare i punti dati.

Passaggio 3: utilizzare la convalida incrociata K-Fold per trovare il modello migliore

Per trovare il valore di estensione ottimale da utilizzare, possiamo eseguire la convalida incrociata k-fold utilizzando le funzioni nel pacchetto caret :

 library (caret)

#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )

#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)

#print results of k-fold cross-validation
print (model)

14 samples
 1 predictor

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 12, 11, 11, 11, 11 
Resampling results across tuning parameters:

  span RMSE Rsquared MAE      
  0.5 10.148315 0.9570137 6.467066
  0.6 7.854113 0.9350278 5.343473
  0.7 6.113610 0.8150066 4.769545
  0.8 17.814105 0.8202561 11.875943
  0.9 26.705626 0.7384931 17.304833

Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.

Possiamo vedere che il valore di span che ha prodotto il valore più basso per l’errore quadratico medio (RMSE) è 0,7 .

Quindi, per il nostro modello di regressione LOESS finale, sceglieremmo di utilizzare un valore di 0,7 per l’argomento span nella funzione loess() .

Risorse addizionali

Le esercitazioni seguenti forniscono informazioni aggiuntive sui modelli di regressione in R:

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come eseguire la regressione logistica in R
Come eseguire la regressione quantile in R
Come eseguire la regressione ponderata in R