Cos'è la regressione curvilinea? (definizione ed esempi)
Regressione curvilinea è il nome dato a qualsiasi modello di regressione che tenta di adattare una curva anziché una linea retta.
Esempi comuni di modelli di regressione curvilinea includono:
Regressione quadratica: utilizzata quando esiste una relazione quadratica tra una variabile predittore e una variabile di risposta . Quando rappresentato graficamente, questo tipo di relazione appare come una “U” o una “U” rovesciata su un grafico a dispersione:
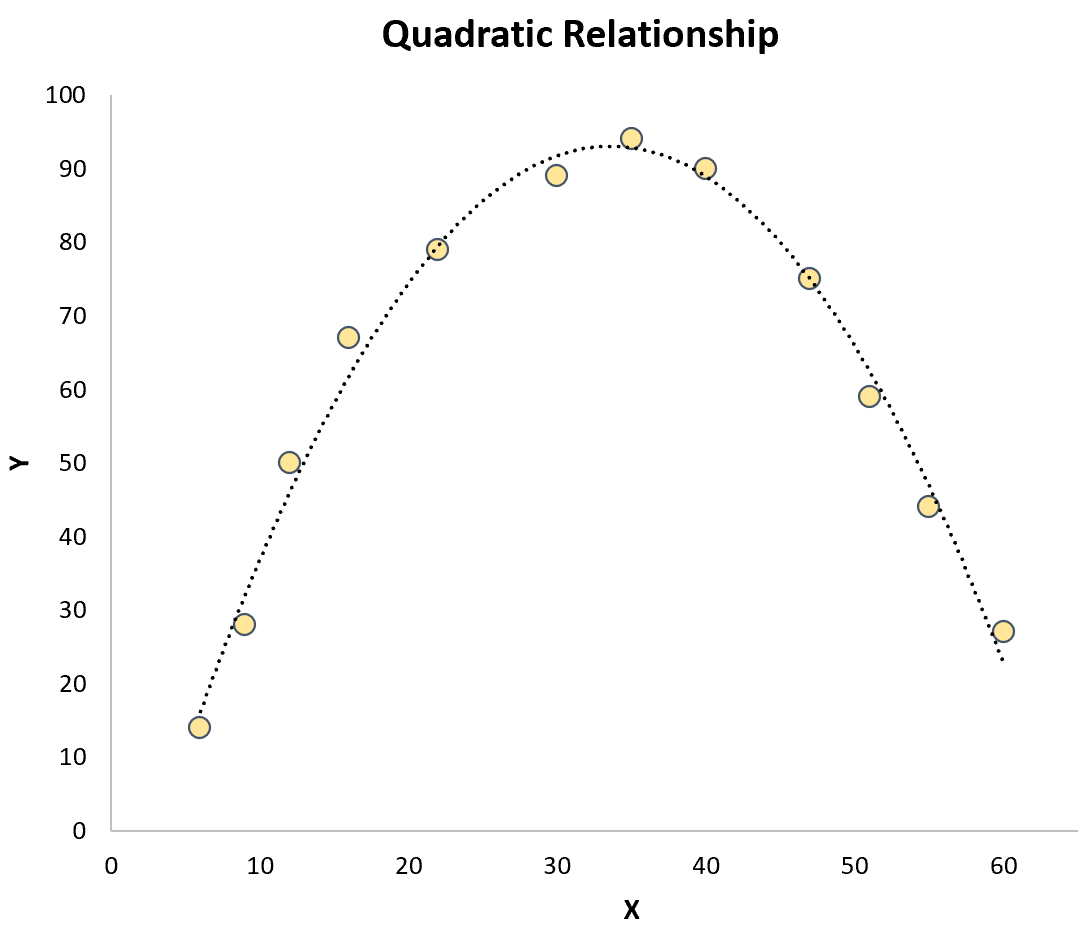
Regressione cubica: utilizzata quando esiste una relazione cubica tra una variabile predittrice e una variabile di risposta. Quando rappresentato graficamente, questo tipo di relazione mostra due curve distinte su un grafico a dispersione:
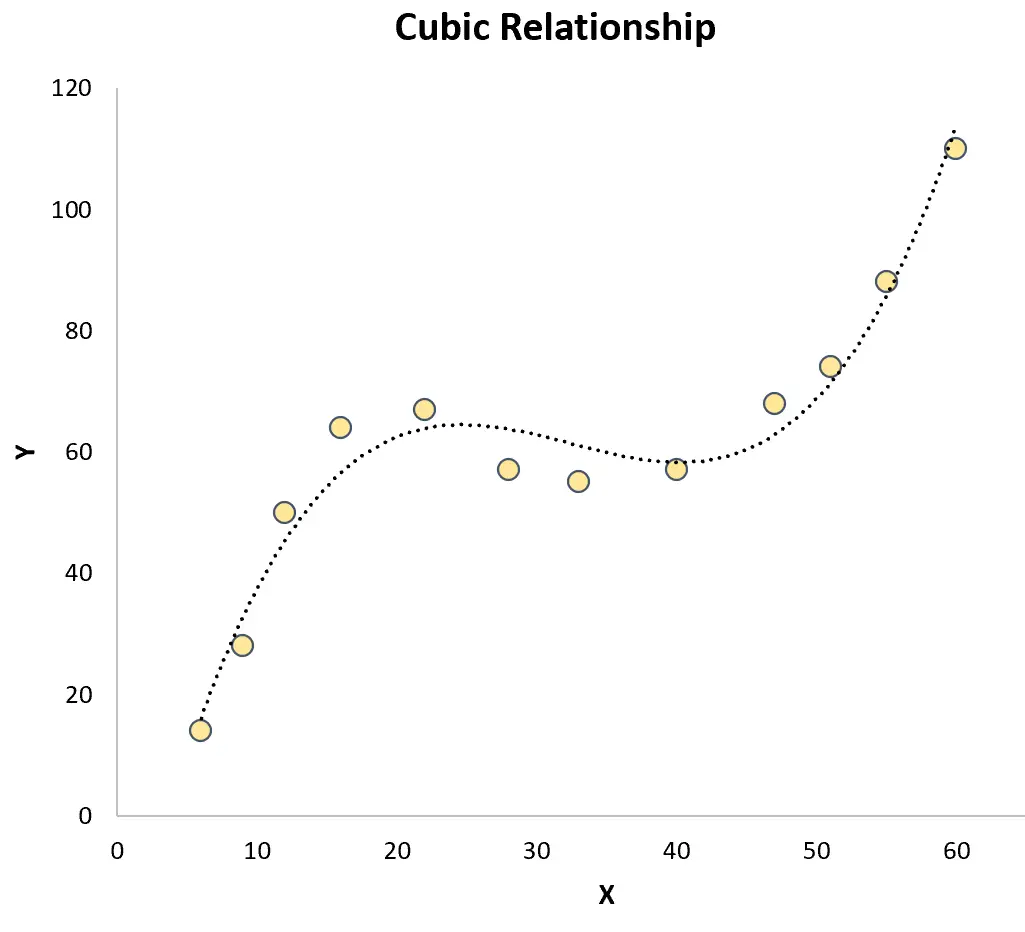
Entrambi contrastano con la regressione lineare semplice in cui la relazione tra la variabile predittore e la variabile risposta è lineare:
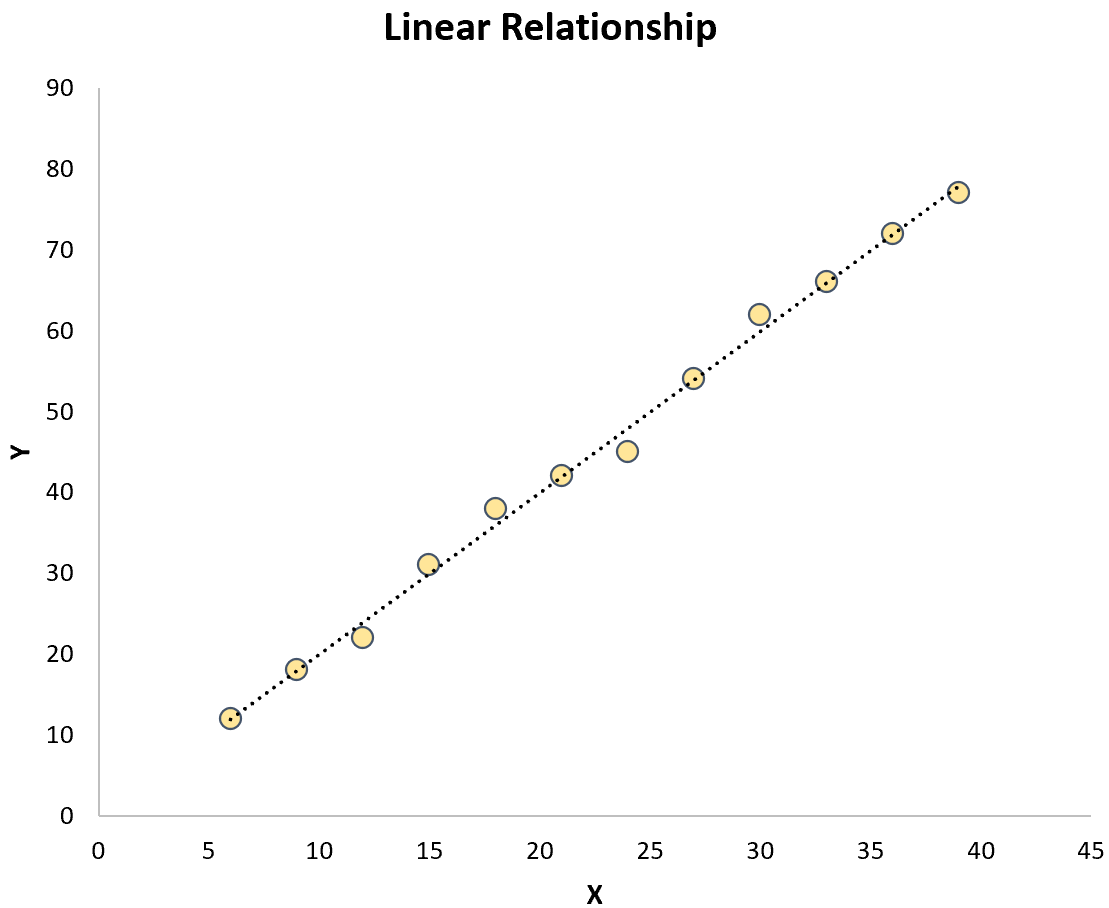
La formula per i modelli di regressione curvilinea
Un semplice modello di regressione lineare tenta di adattare un insieme di dati utilizzando la seguente formula:
ŷ = β 0 + β 1 x
Oro:
- ŷ: La variabile di risposta
- β 0 , β 1 : I coefficienti di regressione
- x: la variabile predittiva
Al contrario, un modello di regressione quadratica utilizza la seguente formula:
ŷ = β 0 + β 1 x + β 2 x 2
E un modello di regressione cubica utilizza la seguente formula:
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
Un nome più generale dato ai modelli di regressione che includono esponenti è regressione polinomiale , che accetta la seguente formula:
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
Il valore di k indica il grado del polinomio. Sebbene il grado possa essere qualsiasi numero positivo, in pratica raramente adattiamo modelli di regressione polinomiale con un grado maggiore di 3 o 4.
Utilizzando gli esponenti nella formula del modello di regressione, i modelli di regressione polinomiale sono in grado di adattare le curve ai set di dati anziché alle linee rette.
Quando utilizzare la regressione curvilinea
Il modo più semplice per sapere se utilizzare o meno la regressione curvilinea è creare un grafico a dispersione della variabile predittore e della variabile risposta.
Se il grafico a dispersione mostra una relazione lineare tra le due variabili, probabilmente è appropriata una semplice regressione lineare.
Tuttavia, se il grafico a dispersione mostra uno schema quadratico, cubico o altro curvilineo tra il predittore e la variabile di risposta, probabilmente è più appropriato utilizzare la regressione curvilinea.
È inoltre possibile adattare un modello di regressione lineare semplice e un modello di regressione curvilinea e confrontare i valori R quadrati adattati di ciascun modello per determinare quale modello fornisce l’adattamento migliore ai dati.
L’R quadrato corretto è utile perché indica quanta varianza nella variabile di risposta può essere spiegata dalle variabili predittive, corrette per il numero di variabili predittive nel modello.
In generale, il modello con il valore R quadrato corretto più alto fornisce un adattamento migliore al set di dati.
Risorse addizionali
I seguenti tutorial spiegano come eseguire la regressione polinomiale in diversi software statistici:
Un’introduzione alla regressione polinomiale
Come eseguire la regressione polinomiale in Excel
Come eseguire la regressione polinomiale in Python
Come eseguire la regressione polinomiale in R
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più