Regressione attraverso l'origine: definizione ed esempio

La regressione lineare semplice è un metodo che può essere utilizzato per quantificare la relazione tra una o più variabili predittive e una variabile di risposta .

Un modello di regressione lineare semplice assume la forma seguente:

y = β ₀ + β ₁ x

Oro:

• y : il valore della variabile di risposta
• β ₀ : il valore della variabile di risposta quando x = 0 (chiamato termine “intercetta”)
• β ₁ : L’aumento medio della variabile di risposta associato a un aumento di un’unità in x
• x : il valore della variabile predittiva

Una versione modificata di questo modello è nota come regressione attraverso l’origine , che forza y ad essere uguale a 0 quando x è uguale a 0.

Questo tipo di modello assume la seguente forma:

y = _β1x

Si noti che il termine di intercetta è stato completamente rimosso dal modello.

Questo modello viene talvolta utilizzato quando i ricercatori sanno che la variabile di risposta deve essere zero quando la variabile predittrice è zero.

Nel mondo reale, questo tipo di modello viene spesso utilizzato negli studi forestali o ecologici .

Ad esempio, i ricercatori possono utilizzare la circonferenza dell’albero per prevederne l’altezza. Se un dato albero ha circonferenza zero, deve avere altezza zero.

Pertanto, quando si adatta un modello di regressione a questi dati, non avrebbe senso che il termine originale fosse diverso da zero.

L’esempio seguente mostra la differenza tra l’adattamento di un modello di regressione lineare semplice ordinario e un modello che implementa la regressione tramite l’origine.

Esempio: regressione attraverso l’origine

Supponiamo che un biologo voglia adattare un modello di regressione utilizzando la circonferenza dell’albero per prevederne l’altezza. Esce e raccoglie le seguenti misurazioni per un campione di 15 alberi:

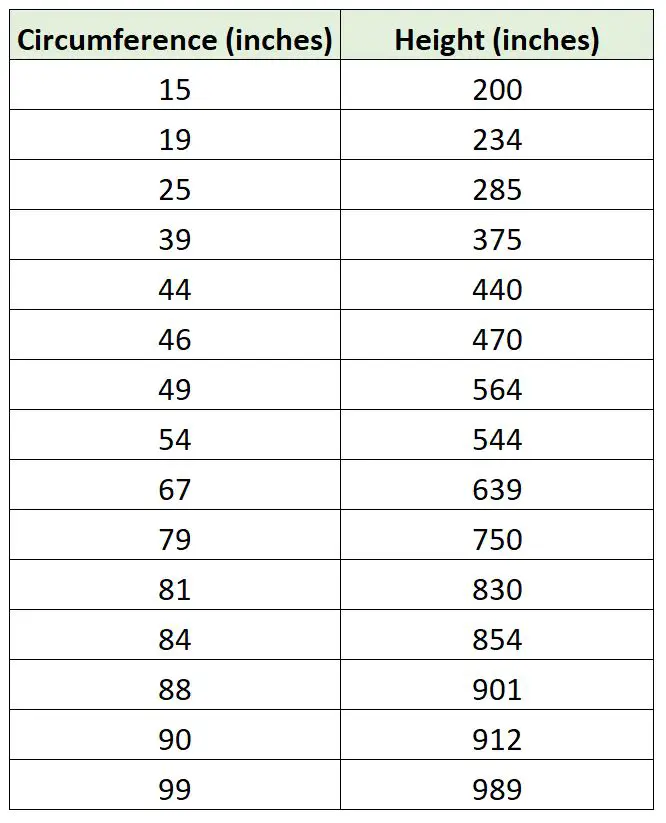
Possiamo utilizzare il seguente codice in R per adattare un modello di regressione lineare semplice con un modello di regressione che non utilizza intercettazioni e tracciare le due linee di regressione:

 #create data frame
df <- data. frame (circ=c(15, 19, 25, 39, 44, 46, 49, 54, 67, 79, 81, 84, 88, 90, 99),
                 height=c(200, 234, 285, 375, 440, 470, 564, 544, 639, 750, 830, 854,
                          901, 912, 989))

#fit a simple linear regression model
model <- lm(height ~ circ, data = df)

#fit regression through the origin
model_origin <- lm(height ~ 0 + ., data = df)

#create scatterplot
plot(df$circ, df$height, xlab=' Circumference ', ylab=' Height ',
     cex= 1.5 , pch= 16 , ylim=c(0.1000), xlim=c(0.100))

#add the fitted regression lines to the scatterplot
abline(model, col=' blue ', lwd= 2 )
abline(model_origin, lty=' dashed ', col=' red ', lwd= 2 )

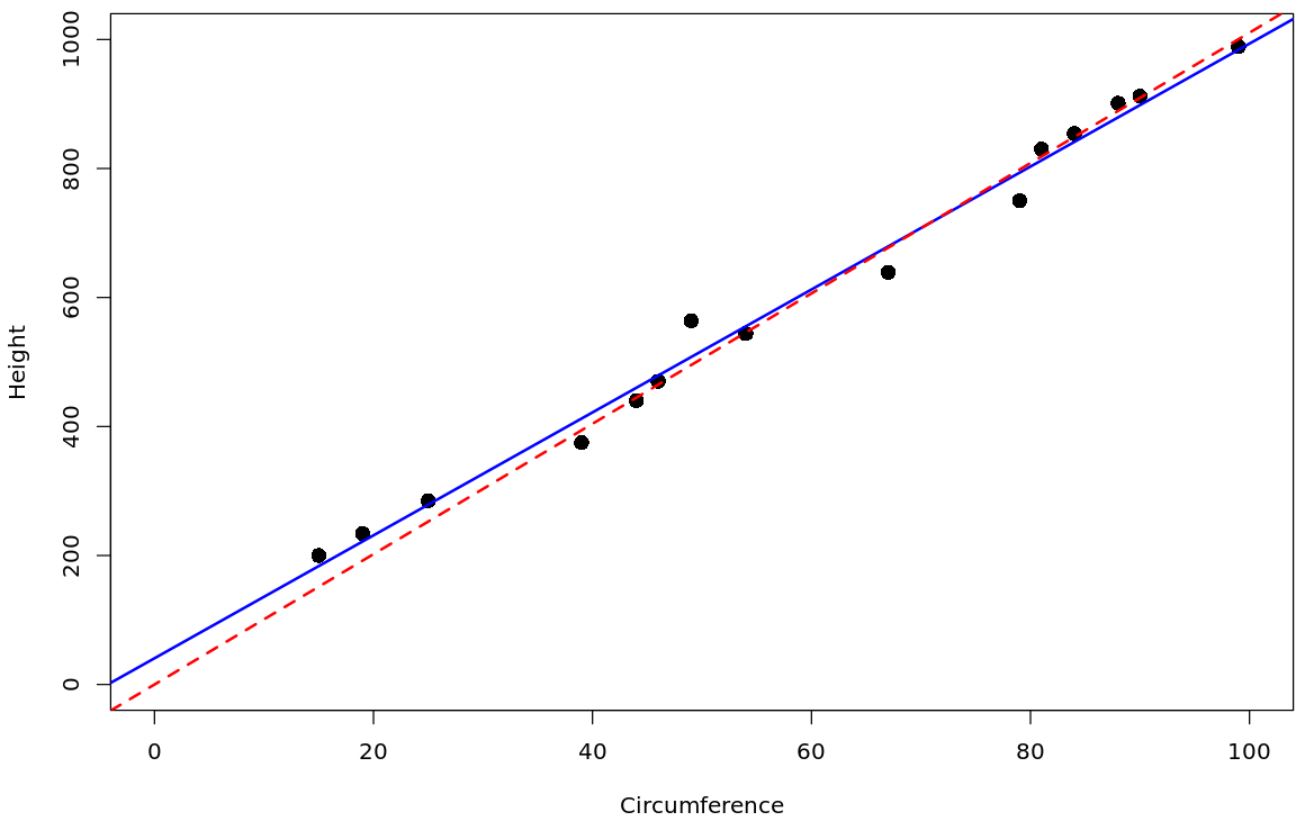
La linea tratteggiata rossa rappresenta il modello di regressione che passa attraverso l’origine e la linea continua blu rappresenta il modello di regressione lineare semplice ordinario.

Possiamo utilizzare il seguente codice in R per ottenere le stime dei coefficienti per ciascun modello:

 #display coefficients for simple linear regression model
coef(model)

(Intercept) circ 
  40.696971 9.529631 

#display coefficients for regression model through the origin
coef(model_origin)

    circ 
10.10574 

L’equazione adattata per il modello di regressione lineare semplice è:

Altezza = 40,6969 + 9,5296 (circonferenza)

E l’equazione adattata per il modello di regressione tramite l’origine è:

Altezza = 10.1057 (circonferenza)

Si noti che le stime dei coefficienti per la variabile circonferenza sono leggermente diverse.

Precauzioni per l’utilizzo della regressione tramite l’origine

Prima di utilizzare la regressione con intercetta, è necessario essere assolutamente sicuri che un valore pari a 0 per la variabile predittore implichi un valore pari a 0 per la variabile di risposta. In molti scenari, è quasi impossibile saperlo con certezza.

E se si utilizza la regressione tramite l’origine per risparmiare un certo grado di libertà nella stima dell’origine, raramente si fa una differenza sostanziale se la dimensione del campione è sufficientemente grande.

Se scegli di utilizzare la regressione tramite l’origine, assicurati di delineare il tuo ragionamento nell’analisi o nel rapporto finale.

Risorse addizionali

Le seguenti esercitazioni forniscono informazioni aggiuntive sulla regressione lineare:

Introduzione alla regressione lineare semplice
Introduzione alla regressione lineare multipla
Come leggere e interpretare una tabella di regressione