Regressione dei componenti principali in python (passo dopo passo)

Dato un insieme di variabili predittive p e una variabile di risposta, la regressione lineare multipla utilizza un metodo noto come minimo quadrato per ridurre al minimo la somma residua dei quadrati (RSS):

RSS = Σ(y _i – ŷ _i ) ²

Oro:

• Σ : simbolo greco che significa somma
• y _i : il valore di risposta effettivo per l’ ^i-esima osservazione
• ŷ _i : il valore di risposta previsto basato sul modello di regressione lineare multipla

Tuttavia, quando le variabili predittive sono altamente correlate, la multicollinearità può diventare un problema. Ciò può rendere inaffidabili le stime dei coefficienti del modello e presentare una varianza elevata.

Un modo per evitare questo problema è utilizzare la regressione delle componenti principali , che trova M combinazioni lineari (chiamate “componenti principali”) dei predittori p originali e quindi utilizza i minimi quadrati per adattare un modello di regressione lineare utilizzando le componenti principali come predittori.

Questo tutorial fornisce un esempio passo passo di come eseguire la regressione dei componenti principali in Python.

Passaggio 1: importa i pacchetti necessari

Per prima cosa importeremo i pacchetti necessari per eseguire la regressione dei componenti principali (PCR) in Python:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn. PCA import decomposition
from sklearn. linear_model import LinearRegression
from sklearn. metrics import mean_squared_error

Passaggio 2: caricare i dati

Per questo esempio utilizzeremo un set di dati chiamato mtcars , che contiene informazioni su 33 auto diverse. Utilizzeremo hp come variabile di risposta e le seguenti variabili come predittori:

• mpg
• Schermo
• merda
• peso
• qsec

Il codice seguente mostra come caricare e visualizzare questo set di dati:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

Passaggio 3: modificare il modello PCR

Il codice seguente mostra come adattare il modello PCR a questi dati. Tieni presente quanto segue:

• pca.fit_transform(scale(X)) : Questo dice a Python che ciascuna delle variabili predittive dovrebbe essere ridimensionata per avere una media pari a 0 e una deviazione standard pari a 1. Ciò garantisce che nessuna variabile predittiva abbia troppa influenza nel modello se questo accade. essere misurato in diverse unità.
• cv = RepeatedKFold() : indica a Python di utilizzare la convalida incrociata k-fold per valutare le prestazioni del modello. Per questo esempio scegliamo k = 10 pieghe, ripetute 3 volte.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#scale predictor variables
pca = pca()
X_reduced = pca. fit_transform ( scale (X))

#define cross validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

regr = LinearRegression()
mse = []

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (regr,
           n.p. ones ((len(X_reduced),1)), y, cv=cv,
           scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    score = -1*model_selection. cross_val_score (regr,
               X_reduced[:,:i], y, cv=cv, scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)
    
# Plot cross-validation results    
plt. plot (mse)
plt. xlabel ('Number of Principal Components')
plt. ylabel ('MSE')
plt. title ('hp') 

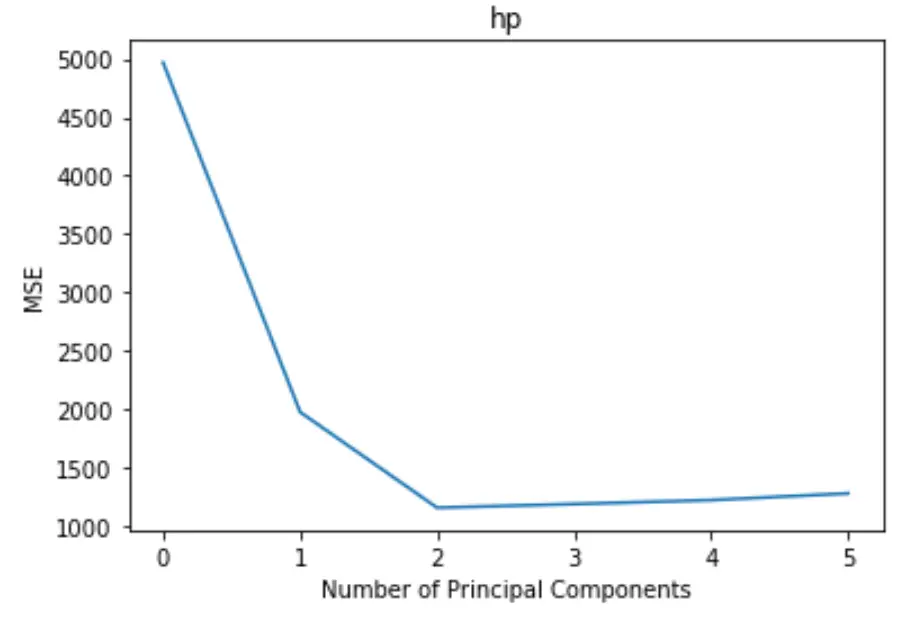
Il grafico mostra il numero di componenti principali lungo l’asse x e il test MSE (errore quadratico medio) lungo l’asse y.

Dal grafico possiamo vedere che l’MSE del test diminuisce aggiungendo due componenti principali, ma inizia ad aumentare quando aggiungiamo più di due componenti principali.

Pertanto, il modello ottimale include solo le prime due componenti principali.

Possiamo anche utilizzare il codice seguente per calcolare la percentuale di varianza nella variabile di risposta spiegata aggiungendo ciascuna componente principale al modello:

 n.p. cumsum (np. round (pca. explained_variance_ratio_ , decimals= 4 )* 100 )

array([69.83, 89.35, 95.88, 98.95, 99.99])

Possiamo vedere quanto segue:

• Utilizzando solo la prima componente principale, possiamo spiegare il 69,83% della variazione della variabile di risposta.
• Aggiungendo la seconda componente principale, possiamo spiegare l’ 89,35% della variazione della variabile di risposta.

Si noti che saremo comunque in grado di spiegare una maggiore varianza utilizzando più componenti principali, ma possiamo vedere che l’aggiunta di più di due componenti principali in realtà non aumenta di molto la percentuale della varianza spiegata.

Passaggio 4: utilizzare il modello finale per fare previsioni

Possiamo utilizzare il modello PCR finale a due componenti principali per fare previsioni su nuove osservazioni.

Il codice seguente mostra come suddividere il set di dati originale in un set di training e un set di test e utilizzare il modello PCR con due componenti principali per fare previsioni sul set di test.

 #split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size= 0.3 , random_state= 0 ) 

#scale the training and testing data
X_reduced_train = pca. fit_transform ( scale (X_train))
X_reduced_test = pca. transform ( scale (X_test))[:,:1]

#train PCR model on training data 
regr = LinearRegression()
reg. fit (X_reduced_train[:,:1], y_train)

#calculate RMSE
pred = regr. predict (X_reduced_test)
n.p. sqrt ( mean_squared_error (y_test, pred))

40.2096

Vediamo che il test RMSE risulta essere 40.2096 . Questa è la deviazione media tra il valore hp previsto e il valore hp osservato per le osservazioni del set di test.

Il codice Python completo utilizzato in questo esempio può essere trovato qui .