Introduzione alla regressione della cresta

Nella regressione lineare multipla ordinaria, utilizziamo un insieme di variabili predittive p e una variabile di risposta per adattare un modello della forma:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Oro:

• Y : la variabile di risposta
• X _j : la j- ^esima variabile predittiva
• β _j : L’effetto medio su Y di un aumento di un’unità in X _j , mantenendo fissi tutti gli altri predittori
• ε : Il termine di errore

I valori di β ₀ , β ₁ , B ₂ , …, β _p vengono scelti utilizzando il metodo dei minimi quadrati , che minimizza la somma dei quadrati dei residui (RSS):

RSS = Σ(y _i – ŷ _i ) ²

Oro:

• Σ : simbolo greco che significa somma
• y _i : il valore di risposta effettivo per l’ ^i-esima osservazione
• ŷ _i : il valore di risposta previsto basato sul modello di regressione lineare multipla

Tuttavia, quando le variabili predittive sono altamente correlate, la multicollinearità può diventare un problema. Ciò può rendere inaffidabili le stime dei coefficienti del modello e presentare una varianza elevata.

Un modo per aggirare questo problema senza rimuovere completamente alcune variabili predittive dal modello è utilizzare un metodo noto come regressione ridge , che cerca invece di ridurre al minimo quanto segue:

RSS + λΣβ _j ²

dove j va da 1 a p e λ ≥ 0.

Questo secondo termine nell’equazione è noto come penalità di ritiro .

Quando λ = 0, questo termine di penalità non ha alcun effetto e la regressione della cresta produce le stesse stime dei coefficienti dei minimi quadrati. Tuttavia, quando λ si avvicina all’infinito, la penalità di contrazione diventa più influente e le stime del coefficiente di regressione di picco si avvicinano allo zero.

In generale, le variabili predittive meno influenti nel modello diminuiranno verso lo zero più velocemente.

Perché utilizzare la regressione della cresta?

Il vantaggio della regressione Ridge rispetto alla regressione dei minimi quadrati è il compromesso bias-varianza .

Ricordiamo che l’errore quadratico medio (MSE) è una metrica che possiamo utilizzare per misurare l’accuratezza di un determinato modello e viene calcolata come segue:

MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE = Varianza + Bias ² + Errore irriducibile

L’idea di base della regressione Ridge è quella di introdurre una piccola distorsione in modo che la varianza possa essere significativamente ridotta, portando a un MSE complessivo inferiore.

Per illustrare ciò, si consideri il seguente grafico:

Si noti che all’aumentare di λ, la varianza diminuisce in modo significativo con un aumento molto piccolo della distorsione. Tuttavia, oltre un certo punto, la varianza diminuisce meno rapidamente e la diminuzione dei coefficienti porta ad una loro significativa sottostima, che porta ad un forte aumento della distorsione.

Possiamo vedere dal grafico che l’MSE del test è più basso quando scegliamo un valore per λ che produca un compromesso ottimale tra bias e varianza.

Quando λ = 0, il termine di penalità nella regressione della cresta non ha alcun effetto e quindi produce le stesse stime dei coefficienti dei minimi quadrati. Tuttavia, aumentando λ fino a un certo punto, possiamo ridurre l’MSE complessivo del test.

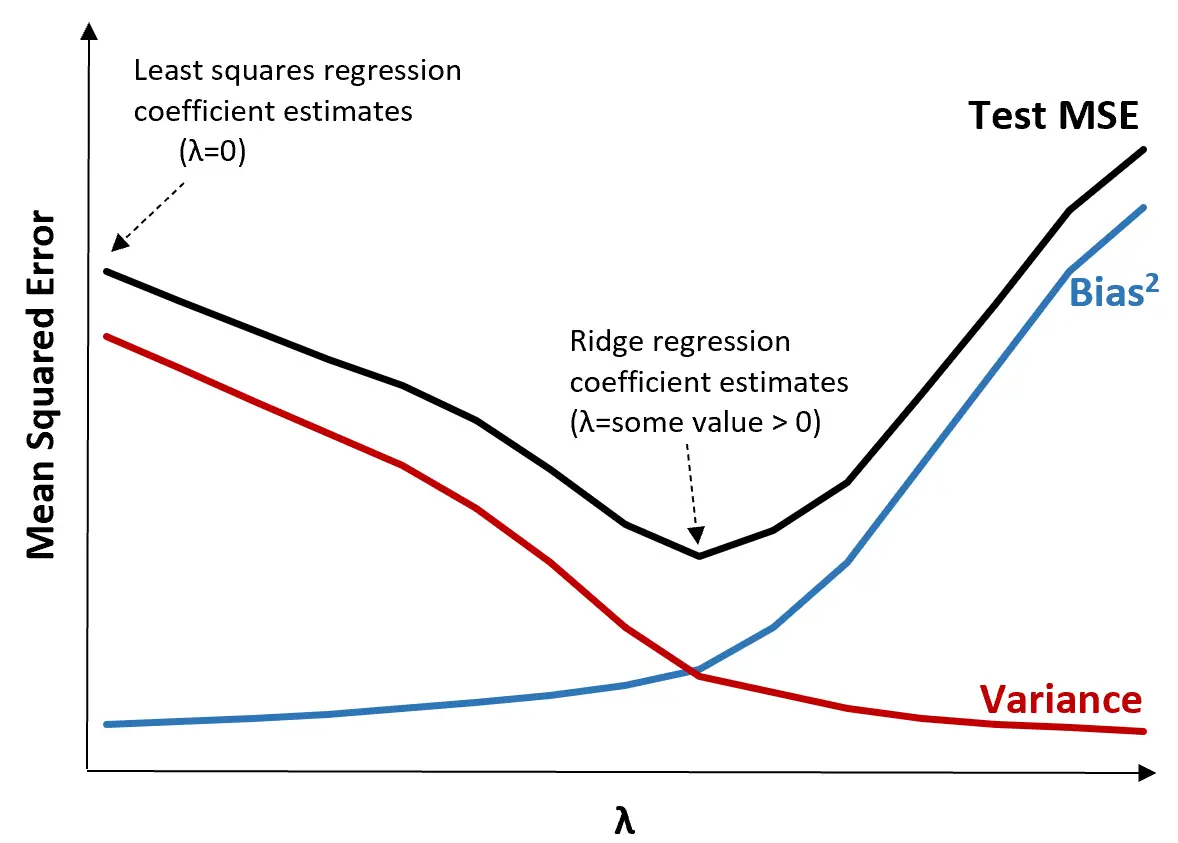
Ciò significa che l’adattamento del modello mediante la regressione della cresta produrrà errori di test minori rispetto all’adattamento del modello mediante la regressione dei minimi quadrati.

Passaggi per eseguire la regressione della cresta nella pratica

È possibile utilizzare i seguenti passaggi per eseguire la regressione della cresta:

Passaggio 1: calcolare la matrice di correlazione e i valori VIF per le variabili predittive.

Innanzitutto, dobbiamo produrre una matrice di correlazione e calcolare i valori VIF (fattore di inflazione della varianza) per ciascuna variabile predittrice.

Se rileviamo una forte correlazione tra le variabili predittive e valori VIF elevati (alcuni testi definiscono un valore VIF “alto” come 5 mentre altri usano 10), allora la regressione della cresta è probabilmente appropriata.

Tuttavia, se nei dati non è presente multicollinearità, potrebbe non essere necessario eseguire innanzitutto la regressione della cresta. Invece, possiamo eseguire la regressione ordinaria dei minimi quadrati.

Passaggio 2: standardizzare ciascuna variabile predittrice.

Prima di eseguire la regressione ridge, è necessario ridimensionare i dati in modo tale che ciascuna variabile predittiva abbia una media pari a 0 e una deviazione standard pari a 1. Ciò garantisce che nessuna singola variabile predittiva abbia un’influenza eccessiva durante l’esecuzione di una regressione ridge.

Passaggio 3: adattare il modello di regressione della cresta e scegliere un valore per λ.

Non esiste una formula esatta che possiamo usare per determinare quale valore usare per λ. In pratica, ci sono due modi comuni per scegliere λ:

(1) Creare un grafico della traccia della cresta. Questo è un grafico che visualizza i valori dei coefficienti stimati all’aumentare di λ verso l’infinito. Tipicamente, scegliamo λ come il valore al quale la maggior parte delle stime dei coefficienti inizia a stabilizzarsi.

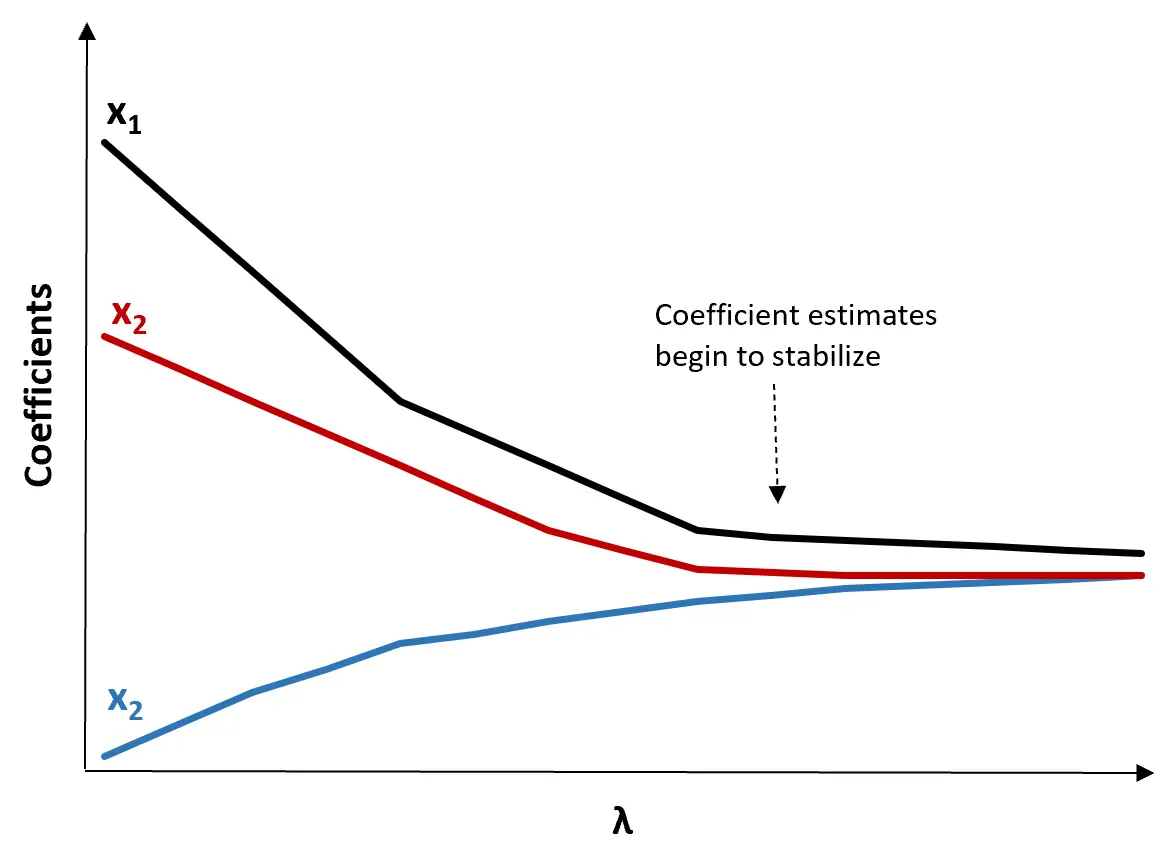
(2) Calcolare il test MSE per ciascun valore di λ.

Un altro modo per scegliere λ è semplicemente calcolare l’MSE di prova di ciascun modello con diversi valori di λ e scegliere λ come valore che produce l’MSE di prova più basso.

Vantaggi e svantaggi della regressione della cresta

Il vantaggio più grande della regressione Ridge è la sua capacità di produrre un errore quadratico medio (MSE) del test inferiore rispetto ai minimi quadrati quando è presente la multicollinearità.

Tuttavia, il più grande svantaggio della regressione Ridge è la sua incapacità di eseguire la selezione delle variabili poiché include tutte le variabili predittive nel modello finale. Poiché alcuni predittori verranno ridotti molto vicino allo zero, ciò può rendere difficile l’interpretazione dei risultati del modello.

In pratica, la regressione Ridge ha il potenziale per produrre un modello in grado di fare previsioni migliori rispetto a un modello dei minimi quadrati, ma spesso è più difficile interpretare i risultati del modello.

A seconda che per te sia più importante l’interpretazione del modello o l’accuratezza della previsione, puoi scegliere di utilizzare i minimi quadrati ordinari o la regressione di cresta in diversi scenari.

Regressione della cresta in R e Python

I seguenti tutorial spiegano come eseguire la regressione della cresta in R e Python, i due linguaggi più comunemente utilizzati per l’adattamento dei modelli di regressione della cresta:

Regressione della cresta in R (passo dopo passo)
Regressione Ridge in Python (passo dopo passo)