Regressione della cresta in r (passo dopo passo)

La regressione della cresta è un metodo che possiamo utilizzare per adattare un modello di regressione quando nei dati è presente la multicollinearità .

In poche parole, la regressione dei minimi quadrati tenta di trovare stime di coefficienti che minimizzino la somma residua dei quadrati (RSS):

RSS = Σ(y _i – ŷ _i )2

Oro:

• Σ : simbolo greco che significa somma
• y _i : il valore di risposta effettivo per l’ ^i-esima osservazione
• ŷ _i : il valore di risposta previsto basato sul modello di regressione lineare multipla

Al contrario, la regressione della cresta cerca di minimizzare quanto segue:

RSS + λΣβ _j ²

dove j va da 1 a p variabili predittive e λ ≥ 0.

Questo secondo termine nell’equazione è noto come penalità di ritiro . Nella regressione della cresta, selezioniamo un valore per λ che produce il test MSE più basso possibile (errore quadratico medio).

Questo tutorial fornisce un esempio passo passo di come eseguire la regressione della cresta in R.

Passaggio 1: caricare i dati

Per questo esempio, utilizzeremo il set di dati integrato di R chiamato mtcars . Utilizzeremo hp come variabile di risposta e le seguenti variabili come predittori:

• mpg
• peso
• merda
• qsec

Per eseguire la regressione ridge, utilizzeremo le funzioni del pacchetto glmnet . Questo pacchetto richiede che la variabile di risposta sia un vettore e che l’insieme di variabili predittive sia della classe data.matrix .

Il codice seguente mostra come definire i nostri dati:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

Passaggio 2: adattare il modello di regressione Ridge

Successivamente, utilizzeremo la funzione glmnet() per adattare il modello di regressione Ridge e specificheremo alpha=0 .

Si noti che impostare alpha uguale a 1 equivale a utilizzare la regressione Lazo e impostare alpha su un valore compreso tra 0 e 1 equivale a utilizzare una rete elastica.

Si noti inoltre che la regressione ridge richiede che i dati siano standardizzati in modo tale che ciascuna variabile predittiva abbia una media pari a 0 e una deviazione standard pari a 1.

Fortunatamente, glmnet() esegue automaticamente questa standardizzazione per te. Se hai già standardizzato le variabili, puoi specificare standardize=False .

 library (glmnet)

#fit ridge regression model
model <- glmnet(x, y, alpha = 0 )

#view summary of model
summary(model)

          Length Class Mode   
a0 100 -none- numeric
beta 400 dgCMatrix S4     
df 100 -none- numeric
dim 2 -none- numeric
lambda 100 -none- numeric
dev.ratio 100 -none- numeric
nulldev 1 -none- numeric
npasses 1 -none- numeric
jerr 1 -none- numeric
offset 1 -none- logical
call 4 -none- call   
nobs 1 -none- numeric

Passaggio 3: scegli un valore ottimale per Lambda

Successivamente, identificheremo il valore lambda che produce l’errore quadratico medio (MSE) più basso del test utilizzando la convalida incrociata k-fold .

Fortunatamente, glmnet ha la funzione cv.glmnet() che esegue automaticamente la convalida incrociata k-fold utilizzando k = 10 volte.

 #perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 0 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 10.04567

#produce plot of test MSE by lambda value
plot(cv_model) 

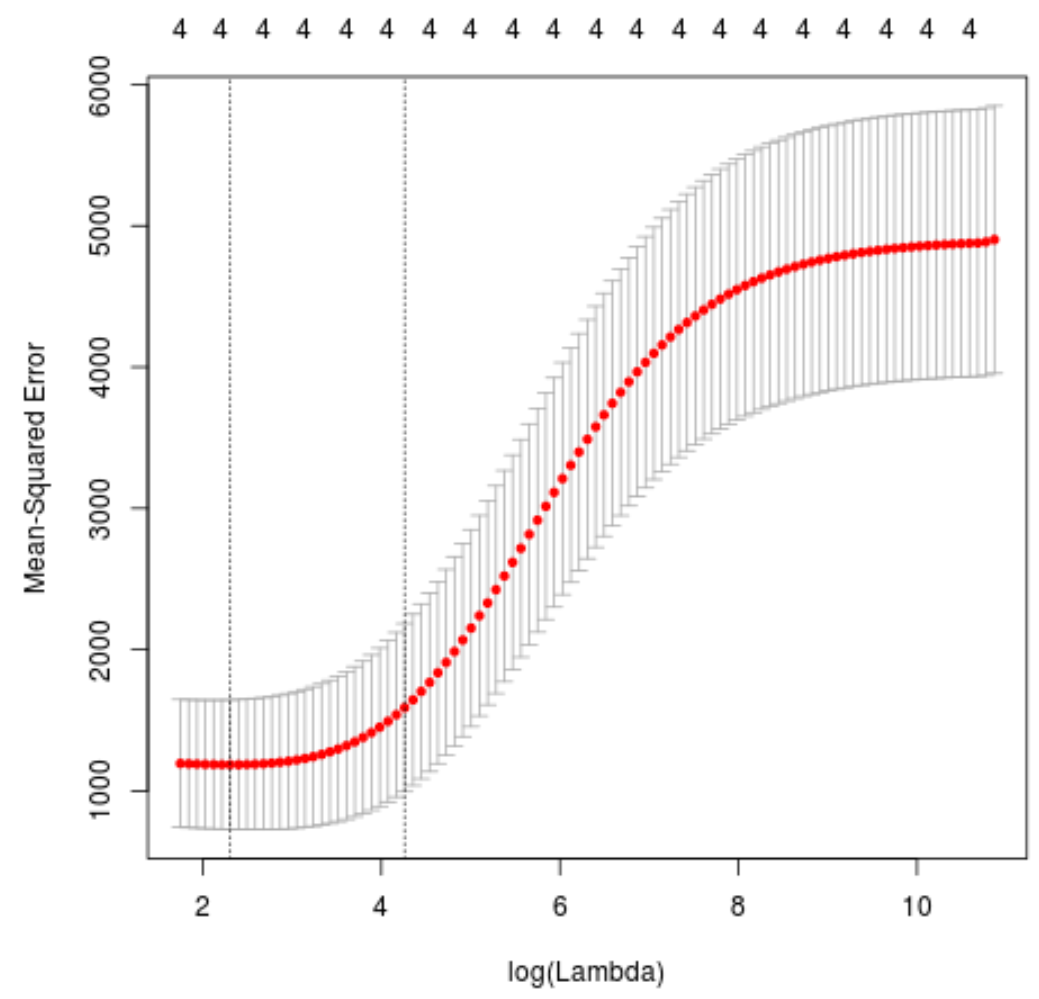
Il valore lambda che minimizza il test MSE risulta essere 10.04567 .

Passaggio 4: analizzare il modello finale

Infine, possiamo analizzare il modello finale prodotto dal valore lambda ottimale.

Possiamo utilizzare il seguente codice per ottenere le stime dei coefficienti per questo modello:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 0 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                    s0
(Intercept) 475.242646
mpg -3.299732
wt 19.431238
drat -1.222429
qsec -17.949721

Possiamo anche produrre un grafico Trace per visualizzare come sono cambiate le stime dei coefficienti a causa dell’aumento di lambda:

 #produce Ridge trace plot
plot(model, xvar = " lambda ") 

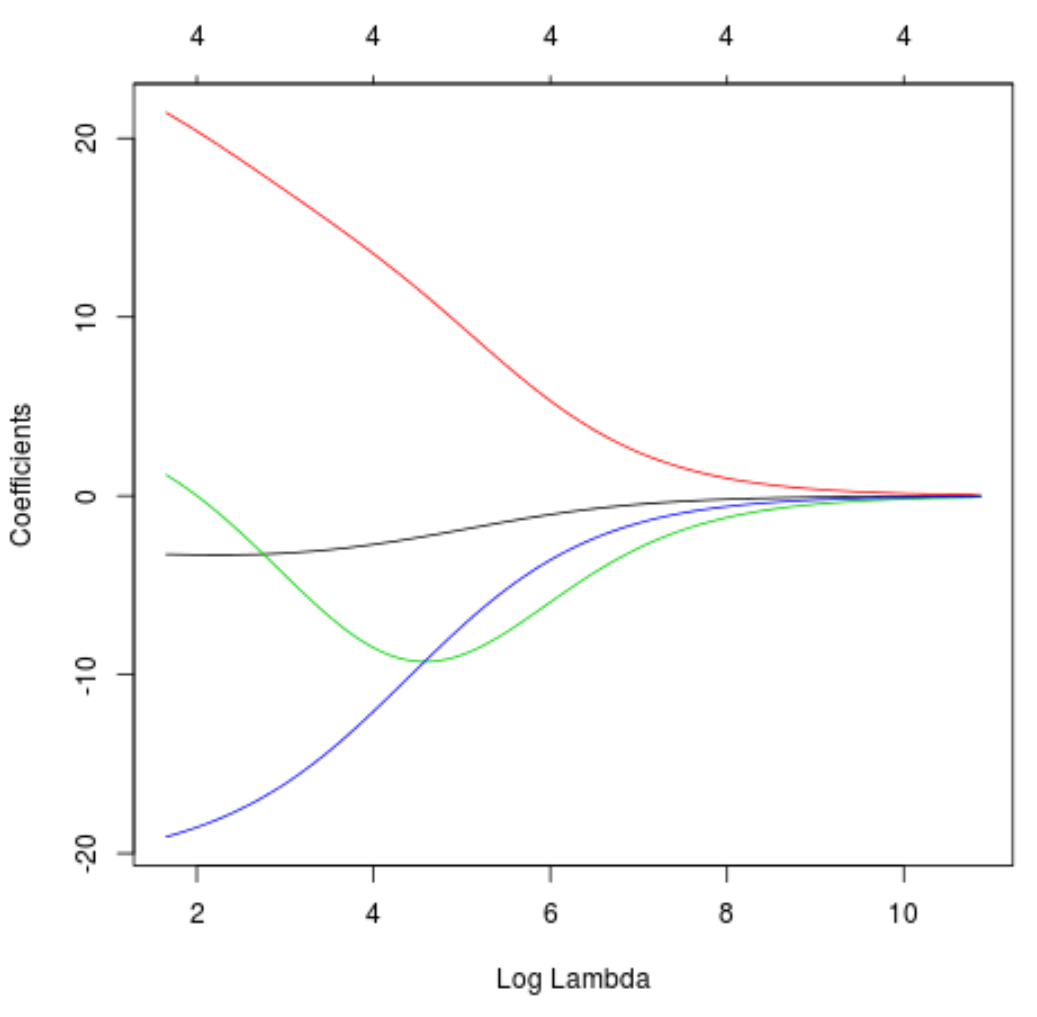
Infine, possiamo calcolare l’ R quadrato del modello sui dati di addestramento:

 #use fitted best model to make predictions
y_predicted <- predict (model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.7999513

La R al quadrato risulta essere 0,7999513 . Cioè, il modello migliore è stato in grado di spiegare il 79,99% della variazione nei valori di risposta dei dati di addestramento.

Puoi trovare il codice R completo utilizzato in questo esempio qui .