Come eseguire la regressione di potenza in r (passo dopo passo)

La regressione su potenza è un tipo di regressione non lineare che assume la forma seguente:

y = ^axb

Oro:

• y: la variabile di risposta
• x: la variabile predittiva
• a, b: i coefficienti di regressione che descrivono la relazione tra x e y

Questo tipo di regressione viene utilizzato per modellare situazioni in cui la variabile di risposta è uguale alla variabile predittore elevata a una potenza.

Il seguente esempio passo passo mostra come eseguire una regressione di potenza per un dato set di dati in R.

Passaggio 1: creare i dati

Innanzitutto, creiamo dati falsi per due variabili: x e y.

 #create data
x=1:20
y=c(1, 8, 5, 7, 6, 20, 15, 19, 23, 37, 33, 38, 49, 50, 56, 52, 70, 89, 97, 115)

Passaggio 2: visualizzare i dati

Successivamente, creiamo un grafico a dispersione per visualizzare la relazione tra x e y:

 #create scatterplot
plot(x, y) 

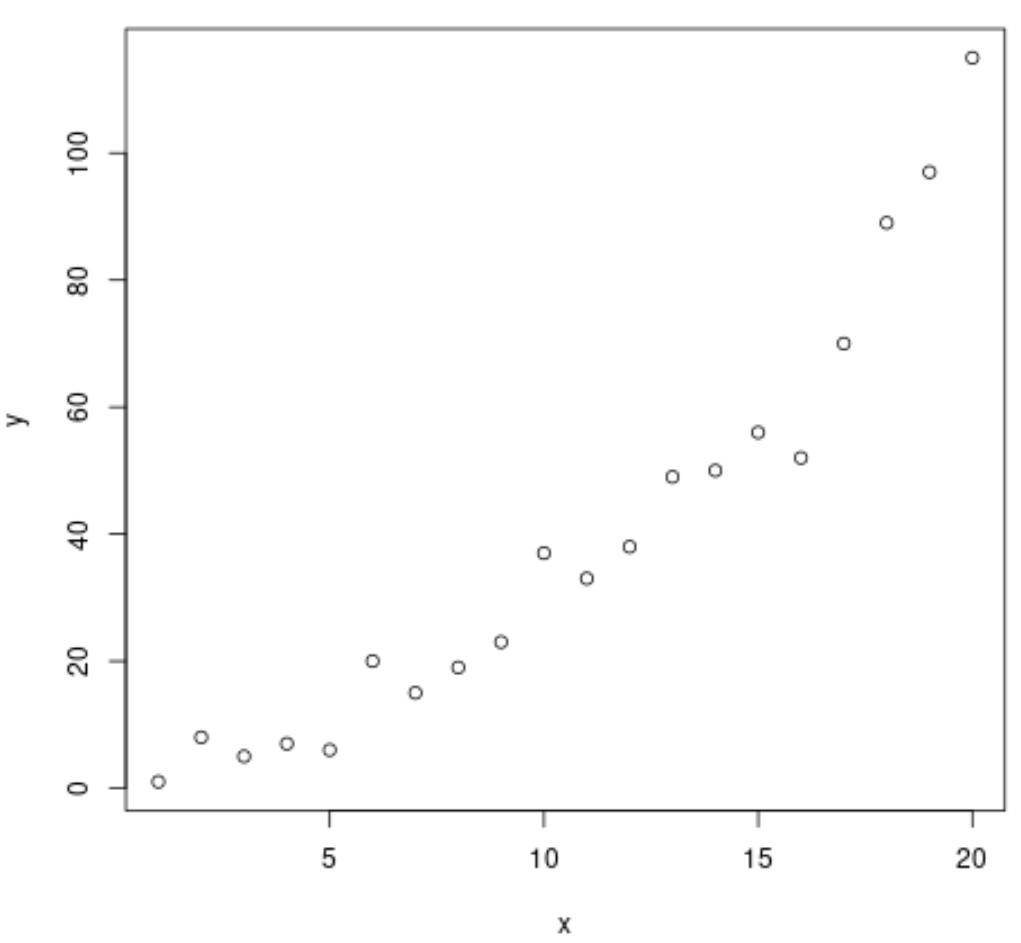
Il grafico mostra che esiste una chiara relazione di potere tra le due variabili. Pertanto, sembra saggio adattare ai dati un’equazione di regressione di potenza piuttosto che un modello di regressione lineare.

Passaggio 3: adattare il modello di regressione della potenza

Successivamente, utilizzeremo la funzione lm() per adattare un modello di regressione ai dati, specificando che R dovrebbe utilizzare la variabile di risposta log e la variabile predittrice log durante l’adattamento del modello:

 #fit the model
model <- lm(log(y)~ log(x))

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ log(x))

Residuals:
     Min 1Q Median 3Q Max 
-0.67014 -0.17190 -0.05341 0.16343 0.93186 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.15333 0.20332 0.754 0.461    
log(x) 1.43439 0.08996 15.945 4.62e-12 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3187 on 18 degrees of freedom
Multiple R-squared: 0.9339, Adjusted R-squared: 0.9302 
F-statistic: 254.2 on 1 and 18 DF, p-value: 4.619e-12

Il valore F complessivo del modello è 252,1 e il valore p corrispondente è estremamente basso (4,619e-12), indicando che il modello nel suo complesso è utile.

Utilizzando i coefficienti della tabella di output, possiamo vedere che l’equazione di regressione della potenza adattata è:

ln(y) = 0,15333 + 1,43439 ln(x)

Applicando e ad entrambi i membri, possiamo riscrivere l’equazione come segue:

• y = ^{e0,15333 + 1,43439ln(x)}
• y = 1,1657x ^1,43439

Possiamo utilizzare questa equazione per prevedere la variabile di risposta, y , in base al valore della variabile predittrice, x .

Ad esempio, se x = 12, allora prevediamo che y sarebbe 41,167 :

y = 1.1657(12) ^1.43439 = 41.167

Bonus: sentiti libero di utilizzare questo calcolatore di regressione di potenza online per calcolare automaticamente l’equazione di regressione di potenza per un determinato predittore e variabile di risposta.

Risorse addizionali

Come eseguire la regressione lineare multipla in R
Come eseguire la regressione esponenziale in R
Come eseguire la regressione logaritmica in R