Come eseguire la regressione lineare multipla in sas

La regressione lineare multipla è un metodo che possiamo utilizzare per comprendere la relazione tra due o più variabili predittive e una variabile di risposta .

Questo tutorial spiega come eseguire la regressione lineare multipla in SAS.

Passaggio 1: creare i dati

Supponiamo di voler adattare un modello di regressione lineare multipla che utilizzi il numero di ore trascorse a studiare e il numero di esami pratici sostenuti per prevedere il voto dell’esame finale degli studenti:

Punteggio esame = β ₀ + β ₁ (ore) + β ₂ (esami preparatori)

Innanzitutto, utilizzeremo il seguente codice per creare un set di dati contenente queste informazioni per 20 studenti:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Passaggio 2: eseguire la regressione lineare multipla

Successivamente, utilizzeremo proc reg per adattare un modello di regressione lineare multipla ai dati:

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

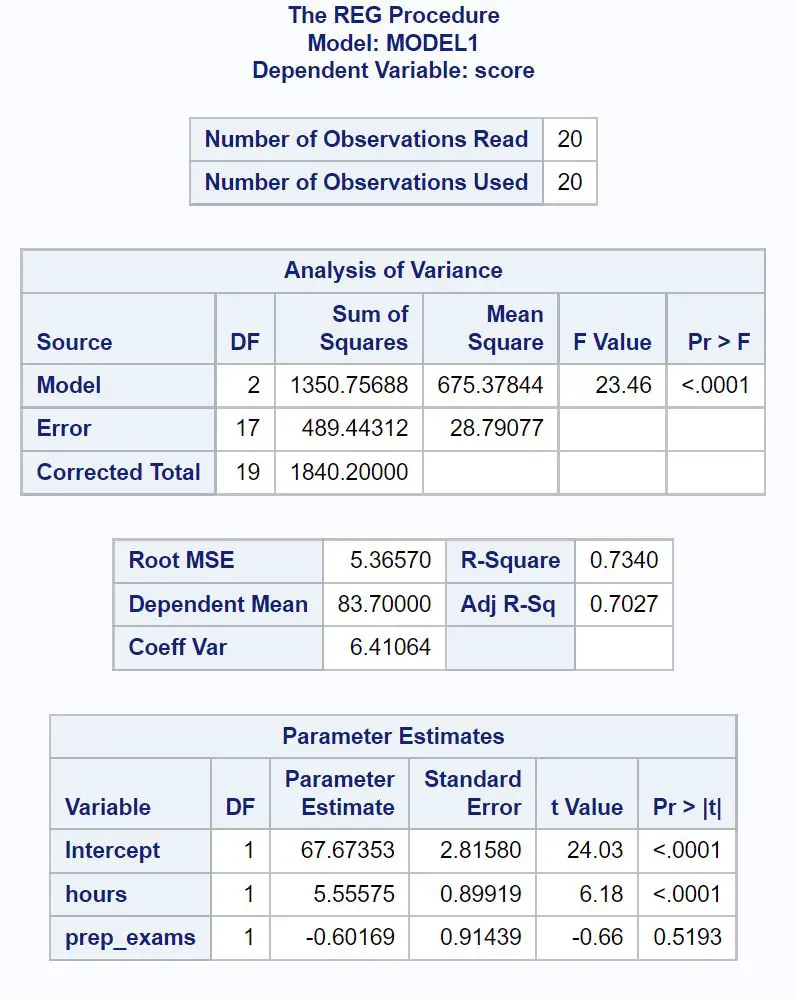
Ecco come interpretare i numeri più rilevanti in ciascuna tabella:

Tabella di analisi degli scostamenti:

Il valore F complessivo del modello di regressione è 23,46 e il valore p corrispondente è <0,0001 .

Poiché questo valore p è inferiore a 0,05, concludiamo che il modello di regressione nel suo insieme è statisticamente significativo.

Tabella di adattamento del modello:

Il valore R-Square ci dice la percentuale di variazione nei punteggi degli esami che può essere spiegata dal numero di ore studiate e dal numero di esami preparatori sostenuti.

In generale, maggiore è il valore R quadrato di un modello di regressione, migliore è la capacità delle variabili predittive di prevedere il valore della variabile di risposta.

In questo caso, il 73,4% della variazione dei punteggi degli esami è spiegabile dal numero di ore studiate e dal numero di esami preparatori sostenuti.

È utile conoscere anche il valore Root MSE . Questo rappresenta la distanza media tra i valori osservati e la retta di regressione.

In questo modello di regressione, i valori osservati si discostano in media di 5,3657 unità dalla retta di regressione.

Tabella delle stime dei parametri:

Possiamo utilizzare i valori di stima dei parametri in questa tabella per scrivere l’equazione di regressione adattata:

Punteggio esame = 67.674 + 5.556*(ore) – 0.602*(prep_exams)

Possiamo utilizzare questa equazione per trovare il punteggio stimato dell’esame di uno studente, in base al numero di ore di studio e al numero di esami pratici che ha sostenuto.

Ad esempio, uno studente che studia per 3 ore e sostiene 2 esami preparatori dovrebbe ricevere un punteggio dell’esame di 83,1 :

Punteggio esame stimato = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

Il valore p per le ore (<0,0001) è inferiore a 0,05, il che significa che ha un’associazione statisticamente significativa con il risultato dell’esame.

Tuttavia, il valore p per gli esami preparatori (0,5193) non è inferiore a 0,05, il che significa che non ha un’associazione statisticamente significativa con il risultato dell’esame.

Potremmo decidere di rimuovere gli esami preparatori dal modello, poiché non sono statisticamente significativi, ed eseguire invece una semplice regressione lineare utilizzando le ore studiate come unica variabile predittiva.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in SAS:

Come calcolare la correlazione in SAS
Come eseguire una regressione lineare semplice in SAS
Come eseguire ANOVA unidirezionale in SAS