Regressione lineare multipla manuale (passo dopo passo)
La regressione lineare multipla è un metodo che possiamo utilizzare per quantificare la relazione tra due o più variabili predittive e una variabile di risposta .
Questo tutorial spiega come eseguire manualmente la regressione lineare multipla.
Esempio: regressione lineare multipla manuale
Supponiamo di avere il seguente set di dati con una variabile di risposta y e due variabili predittive x 1 e x 2 :
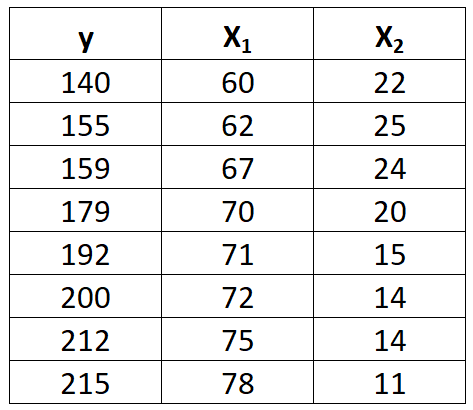
Completare i seguenti passaggi per adattare un modello di regressione lineare multipla a questo set di dati.
Passaggio 1: Calcola x 1 2 , x 2 2 , x 1 y, x 2 y e x 1 x 2 .
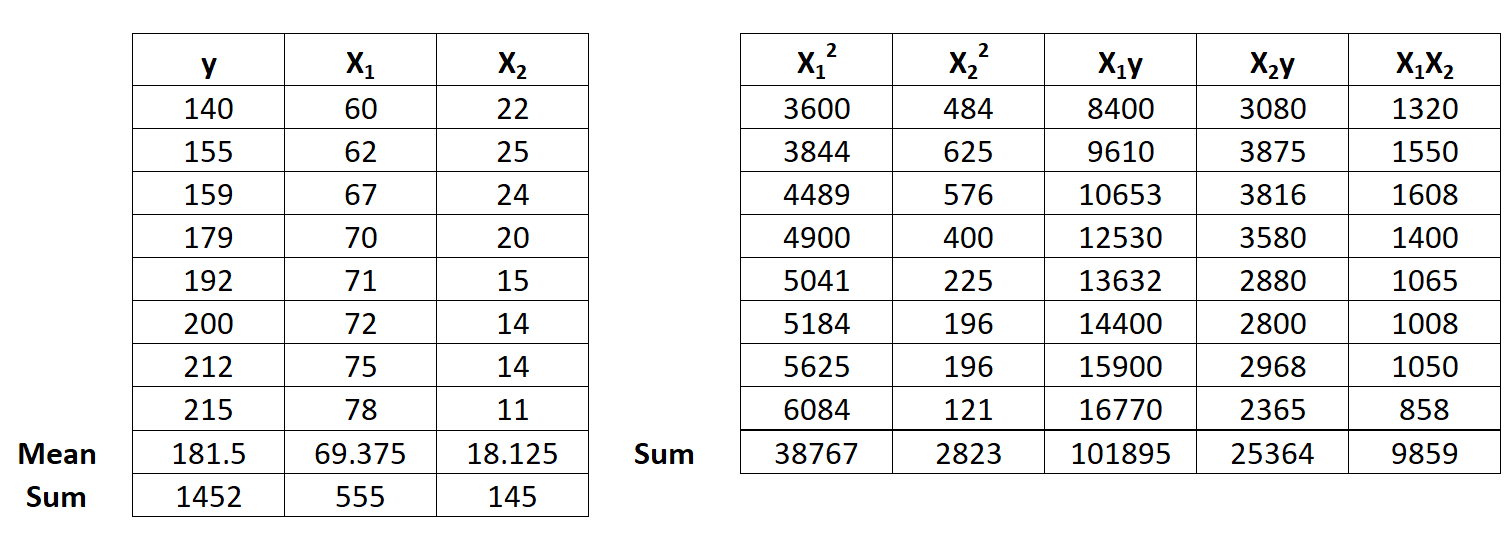
Passaggio 2: calcolare le somme di regressione.
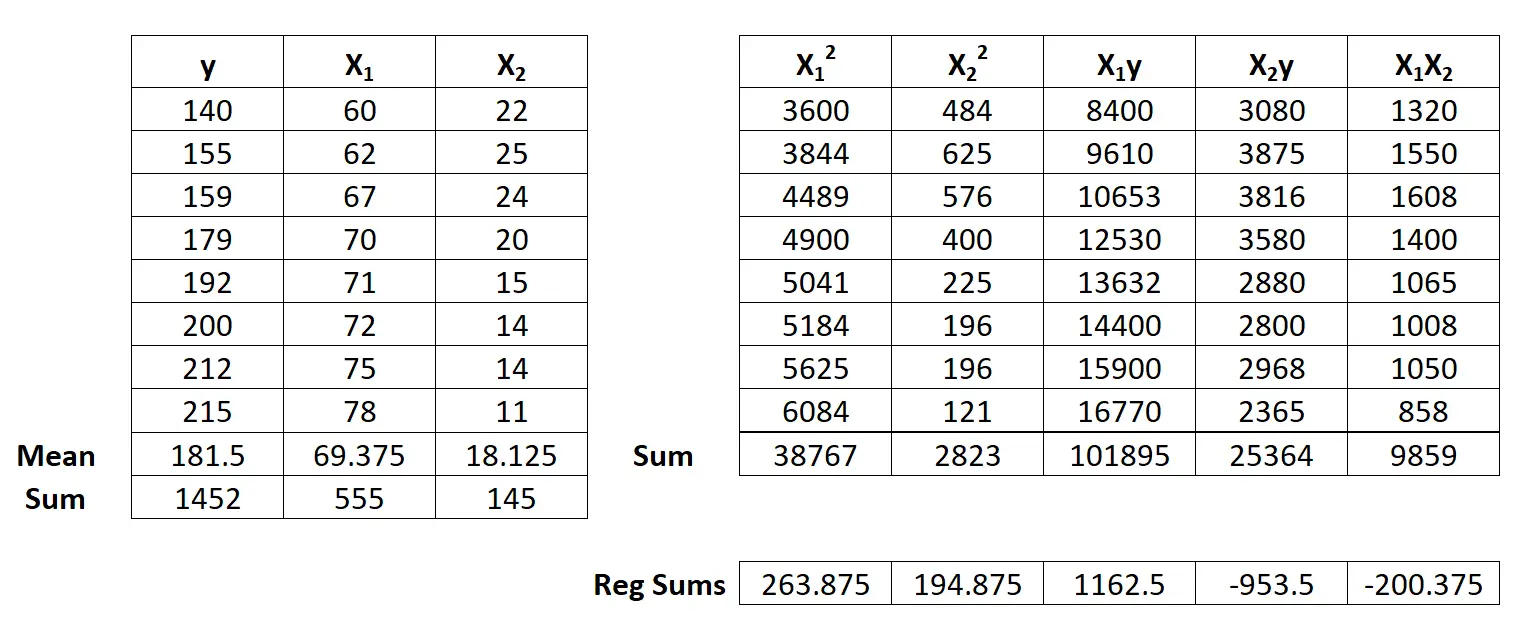
Successivamente, esegui i seguenti calcoli della somma di regressione:
- Σx12 = ΣX12 – ( ΣX1 ) 2 / n = 38,767 – (555) 2 / 8 = 263,875
- Σx22 = ΣX22 – ( ΣX2 ) 2 / n = 2823 – (145) 2 / 8 = 194,875
- Σx1y = Σ _
- Σx2y = Σ _
- Σx1x2 = Σ _ _ _ _
Passaggio 3: Calcola b 0 , b 1 e b 2 .
La formula per calcolare b 1 è: [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Quindi, b 1 = [(194.875)(1162.5) – (-200.375)(-953.5)] / [(263.875) (194.875) – (-200.375) 2 ] = 3.148
La formula per calcolare b 2 è: [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 )(Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Quindi, b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
La formula per calcolare b 0 è: y – b 1 X 1 – b 2 X 2
Pertanto, b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867
Passaggio 5: inserire b 0 , b 1 e b 2 nell’equazione di regressione lineare stimata.
L’equazione di regressione lineare stimata è: ŷ = b 0 + b 1 *x 1 + b 2 *x 2
Nel nostro esempio è ŷ = -6.867 + 3.148x 1 – 1.656x 2
Come interpretare un’equazione di regressione lineare multipla
Ecco come interpretare questa equazione di regressione lineare stimata: ŷ = -6,867 + 3,148x 1 – 1,656x 2
b0 = -6,867 . Quando entrambe le variabili predittive sono uguali a zero, il valore medio di y è -6,867.
b1 = 3.148 . Un aumento di un’unità in x 1 è associato ad un aumento di 3.148 unità in y, in media, assumendo che x 2 rimanga costante.
b2 = -1.656 . Un aumento di un’unità in x 2 è associato a una diminuzione di 1.656 unità in y, in media, assumendo che x 1 rimanga costante.
Risorse addizionali
Un’introduzione alla regressione lineare multipla
Come eseguire manualmente una semplice regressione lineare
Informazioni sull'autore
Benjamin anderson
Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più