Come eseguire la regressione lineare multipla in spss

La regressione lineare multipla è un metodo che possiamo utilizzare per comprendere la relazione tra due o più variabili esplicative e una variabile di risposta.

Questo tutorial spiega come eseguire la regressione lineare multipla in SPSS.

Esempio: regressione lineare multipla in SPSS

Supponiamo di voler sapere se il numero di ore trascorse a studiare e il numero di esami pratici sostenuti influiscono sul voto che uno studente riceve in un determinato esame. Per esplorare questo, possiamo eseguire una regressione lineare multipla utilizzando le seguenti variabili:

Variabili esplicative:

• Ore studiate
• Esami preparatori superati

Variabile di risposta:

• Risultato dell’esame

Utilizzare i passaggi seguenti per eseguire questa regressione lineare multipla in SPSS.

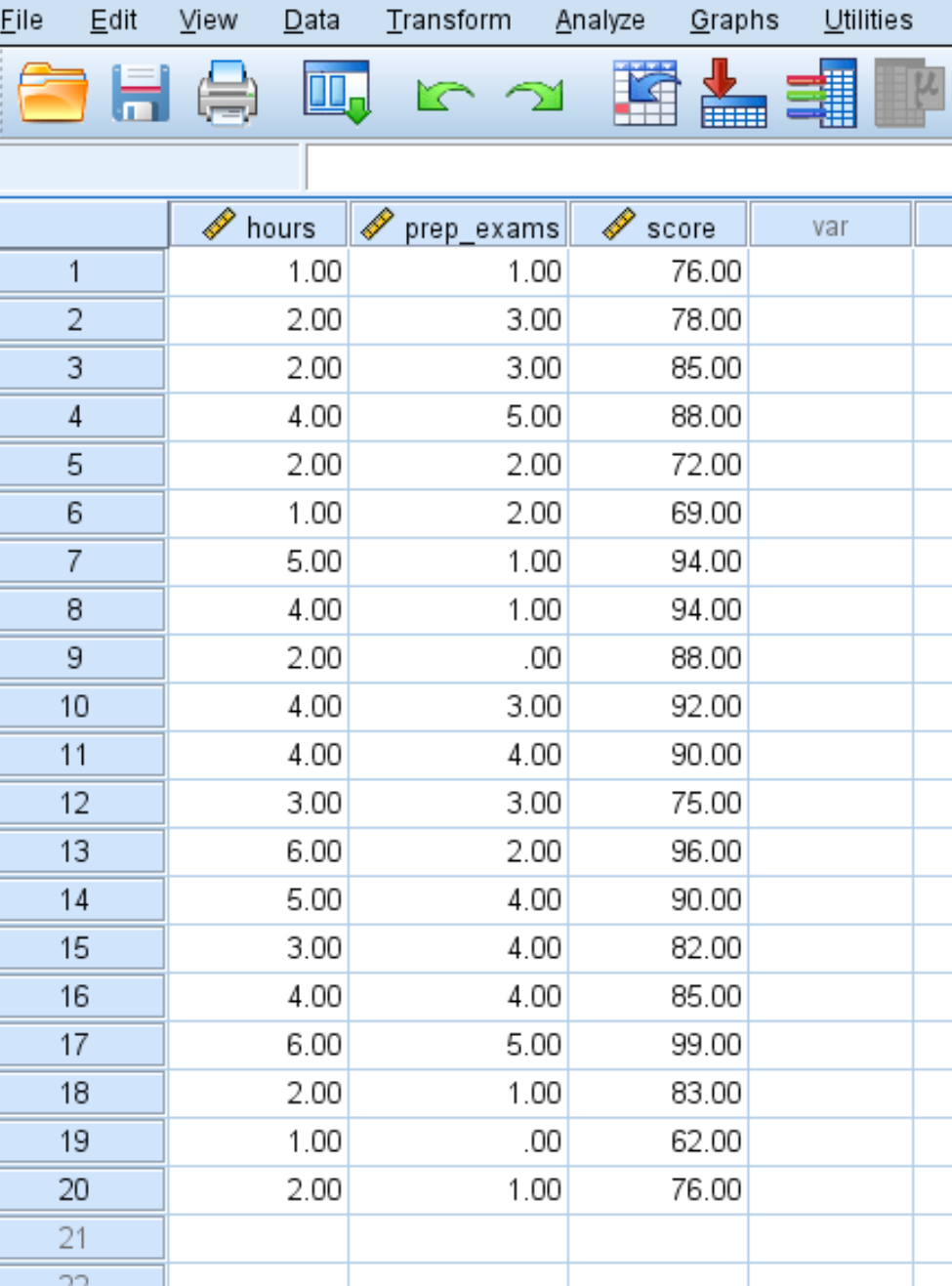
Passaggio 1: inserisci i dati.

Inserire i seguenti dati relativi al numero di ore studiate, esami preparatori sostenuti e risultati esami ricevuti per 20 studenti:

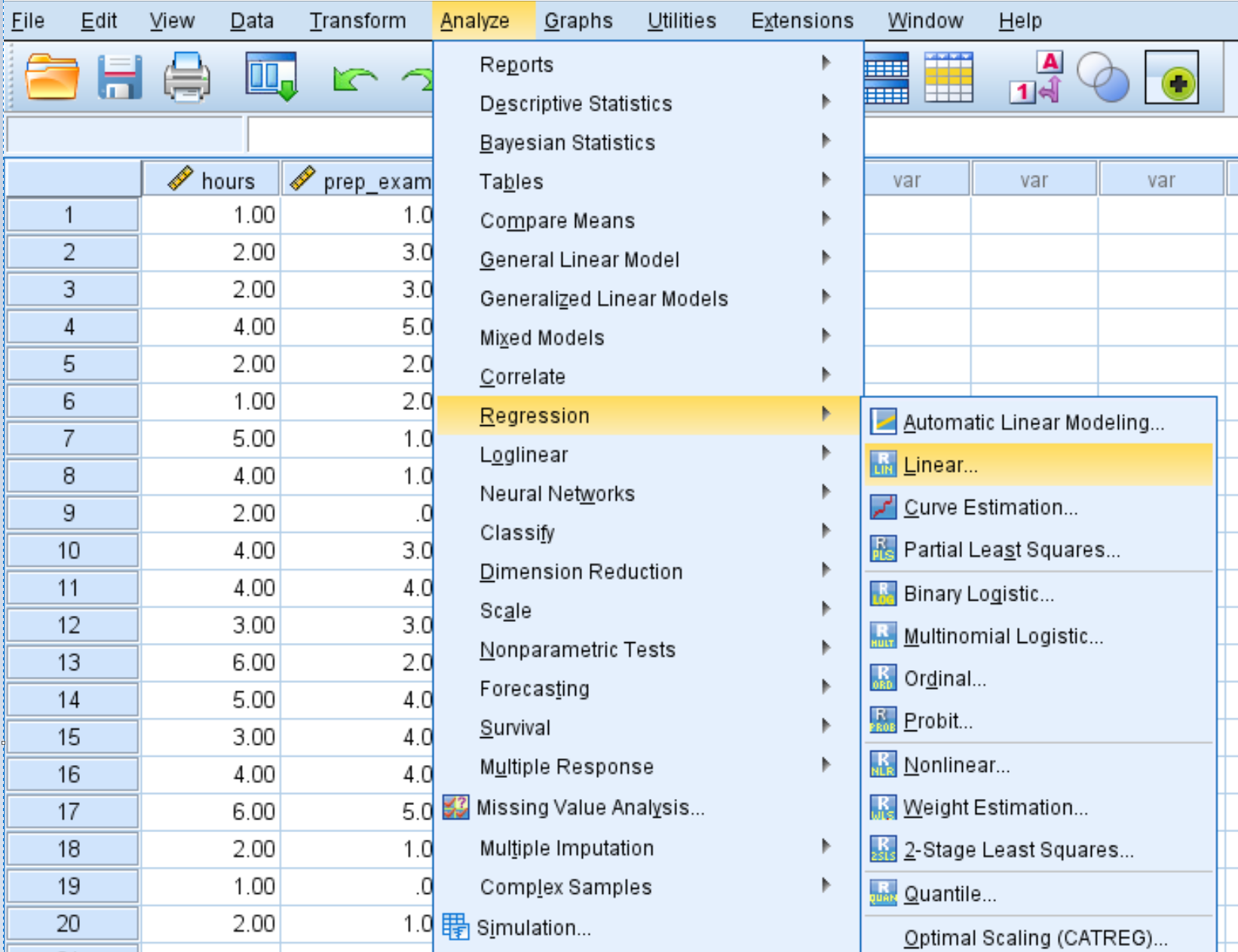
Passaggio 2: eseguire la regressione lineare multipla.

Fare clic sulla scheda Analizza , quindi su Regressione e infine su Lineare :

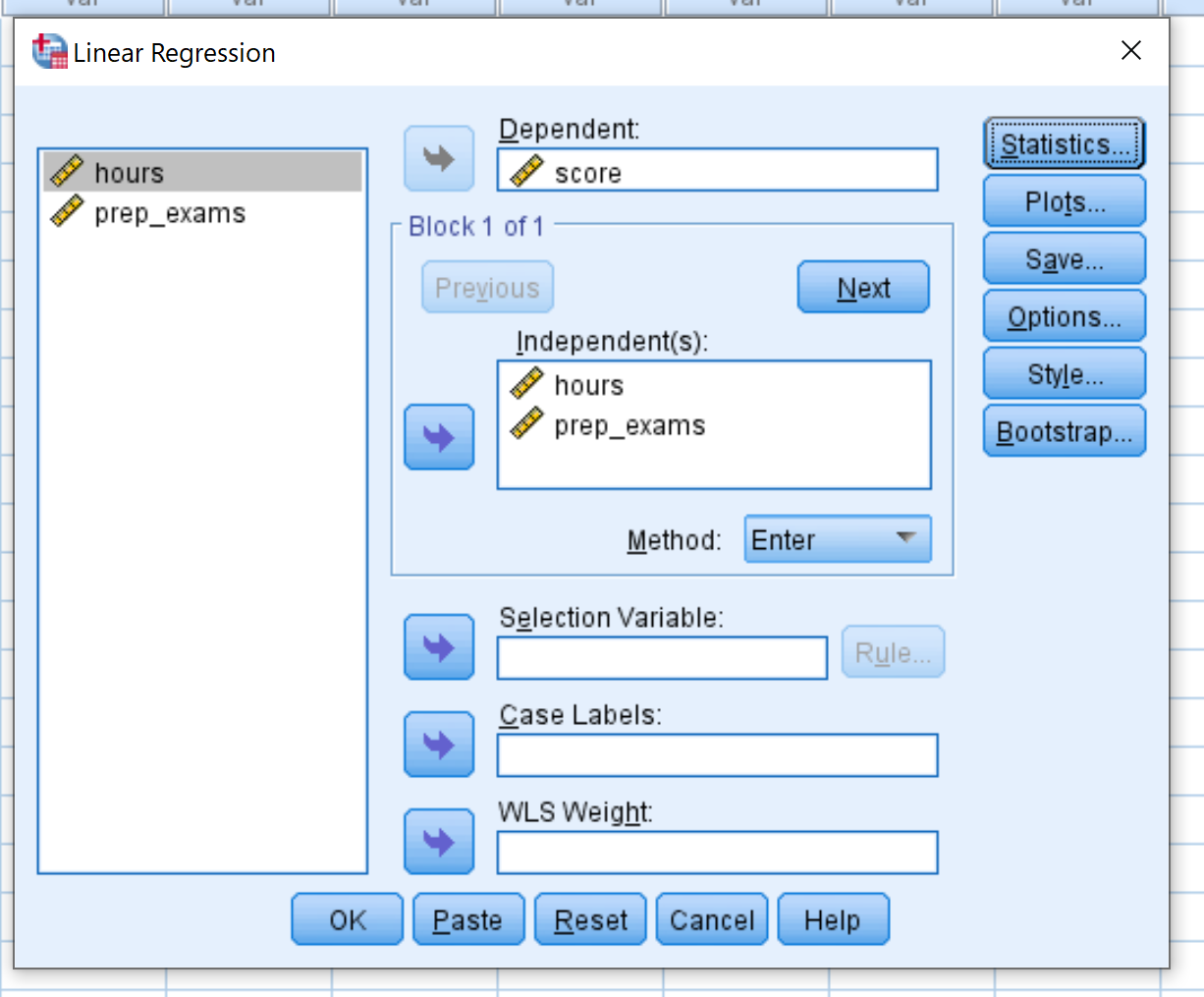
Trascina il punteggio variabile nella casella denominata Dipendente. Trascina le variabili ore e prep_exams nella casella denominata Indipendente/i. Quindi fare clic su OK .

Passaggio 3: interpretare il risultato.

Dopo aver fatto clic su OK , i risultati della regressione lineare multipla verranno visualizzati in una nuova finestra.

La prima tabella che ci interessa si chiama Model Summary :

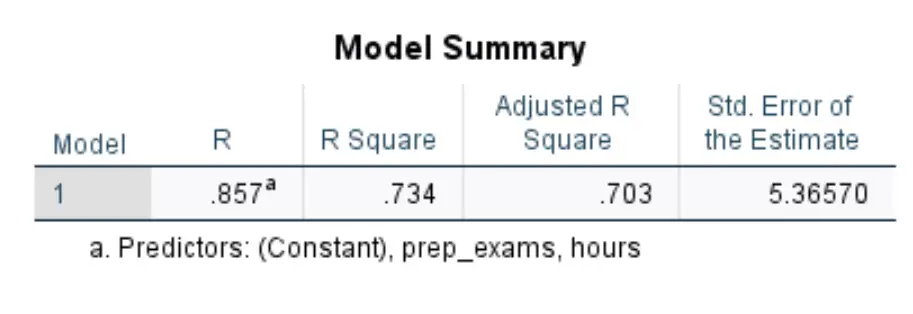
Ecco come interpretare i numeri più rilevanti in questa tabella:

• R quadrato: questa è la proporzione della varianza nella variabile di risposta che può essere spiegata dalle variabili esplicative. In questo esempio, il 73,4% della variazione dei punteggi degli esami può essere spiegata dalle ore studiate e dal numero di esami preparatori sostenuti.
• Standard. Errore di stima: l’errore standard è la distanza media tra i valori osservati e la retta di regressione. In questo esempio i valori osservati si discostano in media di 5.3657 unità dalla retta di regressione.

La prossima tabella che ci interessa si chiama ANOVA :

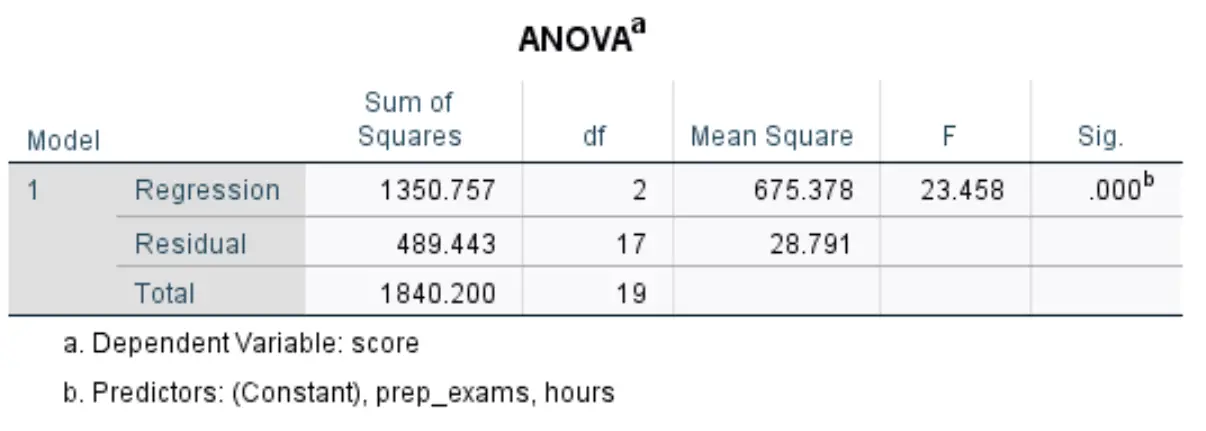
Ecco come interpretare i numeri più rilevanti in questa tabella:

• F: questa è la statistica F complessiva per il modello di regressione, calcolata come regressione quadrata media/residuo quadrato medio.
• Sig: questo è il valore p associato alla statistica F complessiva. Questo ci dice se il modello di regressione nel suo insieme è statisticamente significativo o meno. In altre parole, ci dice se le due variabili esplicative combinate hanno un’associazione statisticamente significativa con la variabile di risposta. In questo caso il p-value è pari a 0,000, il che indica che le variabili esplicative, ore studiate ed esami preparatori sostenuti, hanno un’associazione statisticamente significativa con il risultato dell’esame.

La seguente tabella che ci interessa si intitola Coefficienti :

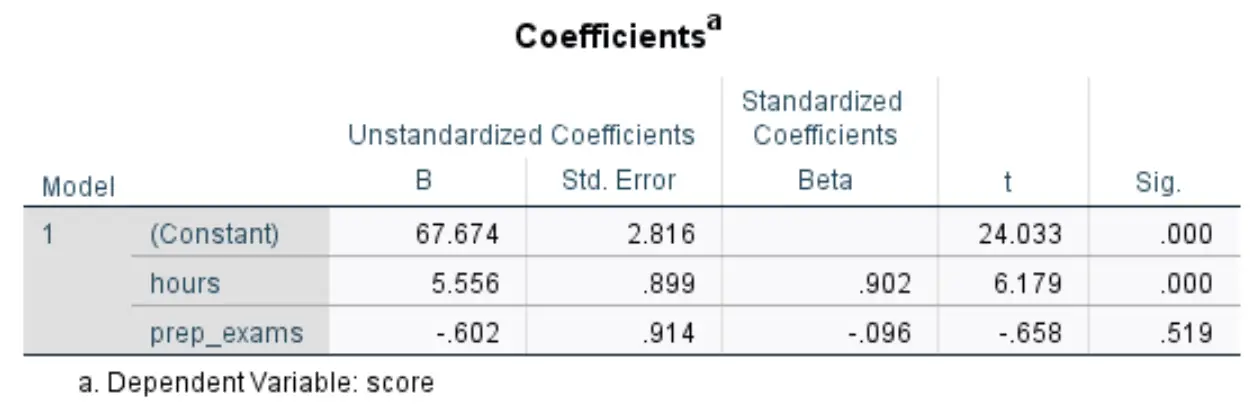
Ecco come interpretare i numeri più rilevanti in questa tabella:

• B non standardizzato (costante): ci dice il valore medio della variabile di risposta quando entrambe le variabili predittive sono zero. In questo esempio, il punteggio medio dell’esame è 67.674 quando le ore studiate e gli esami preparatori sostenuti sono entrambi pari a zero.
• B (ore) non standardizzato: indica la variazione media dei punteggi degli esami associata a un aumento di un’unità delle ore di studio, presupponendo che il numero di esami preparatori sostenuti rimanga costante. In questo caso, ogni ora aggiuntiva dedicata allo studio è associata a un aumento di 5.556 punti nel punteggio dell’esame, assumendo che il numero di esami pratici sostenuti rimanga costante.
• B non standardizzato (prep_exams): indica la variazione media del punteggio dell’esame associata a un aumento di un’unità degli esami preparatori sostenuti, presupponendo che il numero di ore studiate rimanga costante. In questo caso, ad ogni ulteriore esame preparatorio sostenuto è associata una diminuzione di 0,602 punti nel punteggio dell’esame, assumendo che il numero di ore studiate rimanga costante.
• Sig. (ore): questo è il valore p per la variabile esplicativa ore . Poiché questo valore (0,000) è inferiore a 0,05, possiamo concludere che le ore studiate hanno un’associazione statisticamente significativa con i punteggi degli esami.
• Sig. (prep_exams): questo è il valore p per la variabile esplicativa prep_exams . Poiché questo valore (0,519) non è inferiore a 0,05, non possiamo concludere che il numero di esami preparatori sostenuti abbia un’associazione statisticamente significativa con il risultato dell’esame.

Infine, possiamo formare un’equazione di regressione utilizzando i valori mostrati nella tabella per costante , ore e prep_exams . In questo caso l’equazione sarebbe:

Punteggio esame stimato = 67.674 + 5.556*(ore) – 0.602*(prep_exams)

Possiamo utilizzare questa equazione per trovare il punteggio stimato dell’esame di uno studente, in base al numero di ore di studio e al numero di esami pratici che ha sostenuto. Ad esempio, uno studente che studia per 3 ore e sostiene 2 esami preparatori dovrebbe ricevere un punteggio dell’esame di 83,1:

Punteggio esame stimato = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

Nota: poiché la variabile esplicativa per gli esami preparatori non è risultata statisticamente significativa, possiamo decidere di rimuoverla dal modello ed eseguire invece una semplice regressione lineare utilizzando le ore studiate come unica variabile esplicativa.