Regressione lineare semplice

Questo articolo spiega cos’è la regressione lineare semplice nelle statistiche e come viene eseguita. Allo stesso modo, troverai risolto un semplice esercizio di regressione lineare e, inoltre, un semplice calcolatore di regressione lineare online.

Cos’è la regressione lineare semplice?

La regressione lineare semplice è un modello statistico utilizzato per mettere in relazione una variabile indipendente e proviamo ad approssimare la relazione che c’è tra le due variabili.

Pertanto, la regressione lineare semplice viene utilizzata per trovare un’equazione che mette in relazione linearmente due variabili. Logicamente la relazione tra le due variabili deve essere lineare, altrimenti occorre utilizzare un altro tipo di modello di regressione.

L’equazione di un modello di regressione lineare semplice è composta da due coefficienti: la costante dell’equazione (b ₀ ) e il coefficiente di correlazione tra le due variabili (b ₁ ). Pertanto, l’equazione per un modello di regressione lineare semplice è y=b ₀ +b ₁ x.

L’equazione per una regressione lineare semplice è rappresentata graficamente come una linea retta, quindi il coefficiente b ₀ è l’intercetta e il coefficiente b ₁ è la pendenza della linea.

Formule di regressione lineare semplici

Le formule per calcolare i coefficienti di una regressione lineare semplice sono le seguenti:

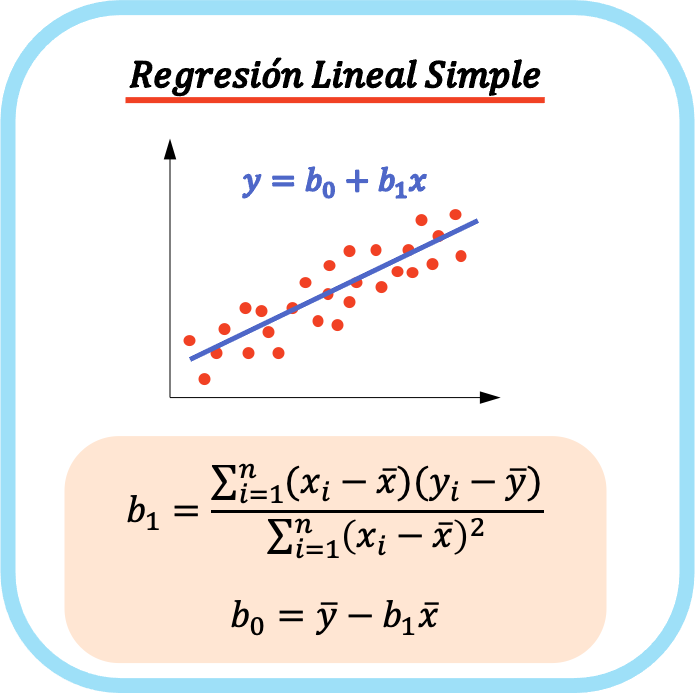
👉 Puoi utilizzare la calcolatrice qui sotto per calcolare i coefficienti di una regressione lineare semplice per qualsiasi set di dati.

Ovviamente, l’equazione risultante dal modello di regressione lineare semplice non sarà in grado di indovinare il valore esatto di tutte le osservazioni, poiché questo modello tenta semplicemente di trovare un’equazione che approssimi la relazione tra le due variabili. Pertanto, il residuo è definito come la differenza tra il valore reale e il valore stimato dal modello di regressione lineare.

Si noti che l’obiettivo di un modello di regressione lineare semplice è ridurre al minimo i quadrati dei residui, ovvero la regressione lineare semplice si basa sul criterio dei minimi quadrati .

Esempio concreto di regressione lineare semplice

Per completare la comprensione del metodo di regressione lineare semplice, ecco un esempio pratico passo dopo passo in cui l’equazione di un modello di regressione lineare semplice viene calcolata da un insieme di dati statistici.

• Dopo aver sostenuto un esame di statistica, a cinque studenti è stato chiesto quante ore di studio avevano dedicato all’esame. I dati sono presentati nella tabella seguente. Eseguire un semplice modello di regressione lineare dei dati statistici raccolti per correlare linearmente le ore di studio al voto raggiunto.

Per realizzare un modello di regressione lineare semplice dobbiamo determinare i coefficienti b ₀ e b ₁ dell’equazione e, per questo, dobbiamo utilizzare le formule viste nella sezione precedente.

Tuttavia, per applicare le semplici formule di regressione lineare, dobbiamo prima calcolare la media della variabile indipendente e la media della variabile dipendente:

Ora che conosciamo le medie delle variabili, calcoliamo il coefficiente b ₁ del modello utilizzando la formula corrispondente:

Infine, calcoliamo il coefficiente b ₀ del modello utilizzando la formula corrispondente:

In breve, l’equazione per il modello di regressione lineare semplice del problema è:

Di seguito è possibile vedere la rappresentazione grafica dei dati campione nonché la retta del modello di regressione lineare semplice:

Infine, una volta calcolata l’equazione del modello di regressione lineare semplice, non resta che interpretare il risultato ottenuto. Per questo è fondamentale calcolare il coefficiente di determinazione del modello di regressione, puoi vedere come si fa cercando l’articolo corrispondente sul nostro sito.

Ipotesi di regressione lineare semplice

Per eseguire una regressione lineare semplice, devono essere soddisfatte le seguenti ipotesi:

• Indipendenza : i residui osservati devono essere indipendenti l’uno dall’altro. Un modo comune per garantire l’indipendenza del modello è aggiungere casualità al processo di campionamento.
• Omoschedasticità : deve esserci omogeneità nelle varianze dei residui, cioè la variabilità dei residui deve essere costante.
• Normalità : i residui devono essere distribuiti normalmente, o in altre parole devono seguire una distribuzione normale con media 0.
• Linearità – La relazione tra la variabile indipendente e la variabile dipendente dovrebbe essere lineare.

Semplice calcolatore di regressione lineare

Inserisci un campione di dati nella calcolatrice qui sotto per adattare un semplice modello di regressione lineare tra due variabili. È necessario separare le coppie di dati, in modo che nella prima casella ci siano solo i valori della variabile indipendente X e nella seconda casella ci siano solo i valori della variabile dipendente Y.

I dati devono essere separati da uno spazio e inseriti utilizzando il punto come separatore decimale.

Regressione lineare semplice e multipla

Infine, vedremo qual è la differenza tra regressione lineare semplice e regressione lineare multipla, poiché sono due tipi di regressioni lineari frequentemente utilizzate in statistica.

La regressione lineare multipla consente di collegare matematicamente due o più variabili esplicative a una variabile di risposta. Cioè, nella regressione lineare multipla, viene creato un modello in cui sono presenti almeno due variabili indipendenti.

Pertanto, la differenza tra regressione lineare semplice e regressione lineare multipla è il numero di variabili indipendenti. Nella regressione lineare semplice esiste una sola variabile indipendente, mentre nella regressione lineare multipla esistono due o più variabili indipendenti.