Come eseguire una regressione lineare semplice in excel

La regressione lineare semplice è un metodo che possiamo utilizzare per comprendere la relazione tra una variabile esplicativa, x, e una variabile di risposta, y.

Questo tutorial spiega come eseguire una semplice regressione lineare in Excel.

Esempio: regressione lineare semplice in Excel

Supponiamo di voler comprendere la relazione tra il numero di ore di studio di uno studente per un esame e il voto ottenuto all’esame.

Per esplorare questa relazione, possiamo eseguire una semplice regressione lineare utilizzando le ore studiate come variabile esplicativa e i punteggi degli esami come variabile di risposta.

Completa i seguenti passaggi in Excel per eseguire una regressione lineare semplice.

Passaggio 1: inserisci i dati.

Inserire i seguenti dati relativi al numero di ore studiate e al punteggio dell’esame ottenuto per 20 studenti:

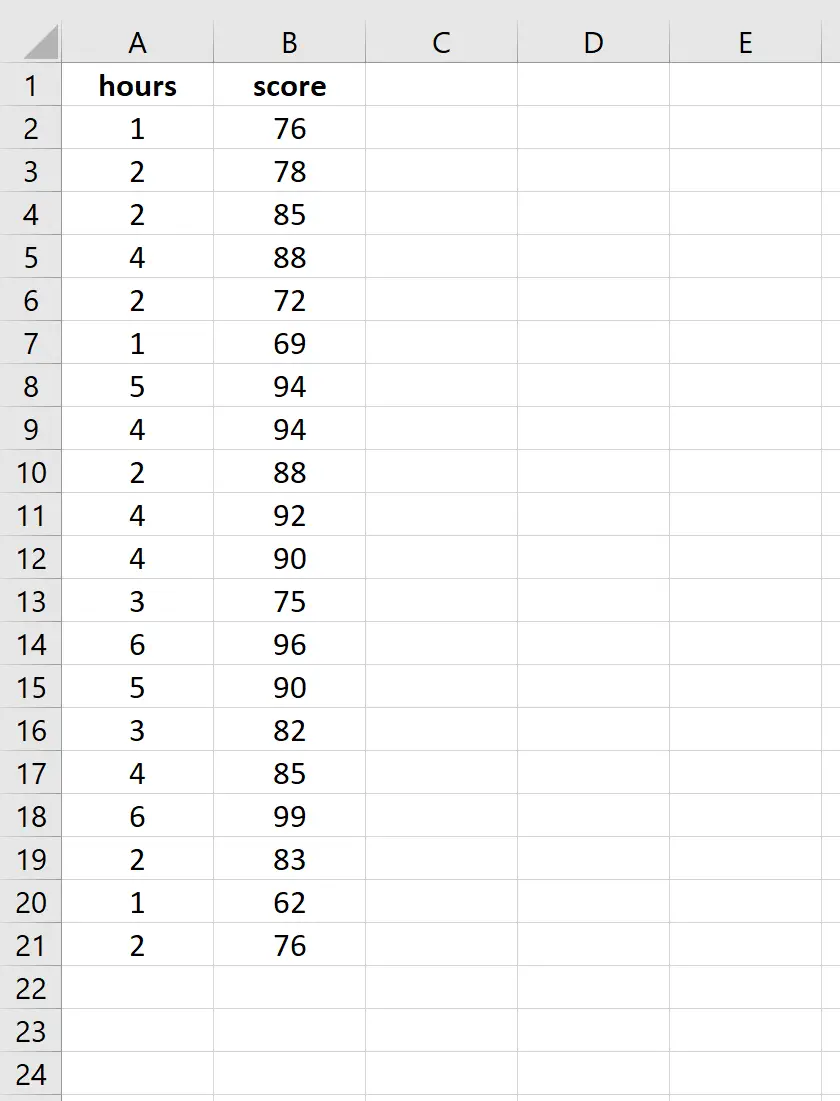
Passaggio 2: visualizzare i dati.

Prima di eseguire una semplice regressione lineare, è utile creare un grafico a dispersione dei dati per garantire che esista effettivamente una relazione lineare tra le ore studiate e il punteggio dell’esame.

Evidenzia i dati nelle colonne A e B. Lungo la barra multifunzione superiore di Excel, vai alla scheda Inserisci . Nel gruppo Grafica , fai clic su Inserisci Scatter (X, Y) e fai clic sulla prima opzione denominata Scatter . Ciò produrrà automaticamente la seguente nuvola di punti:

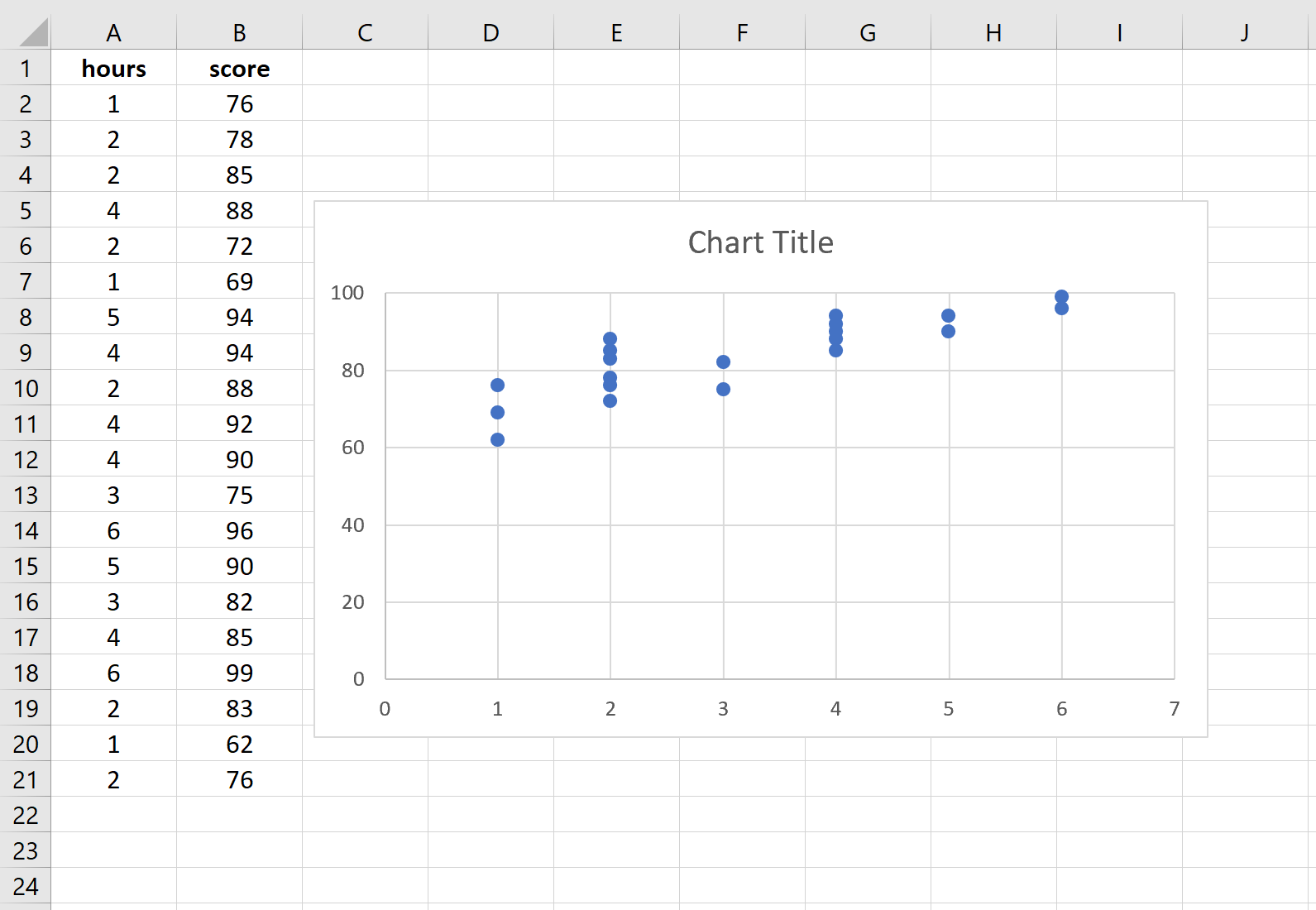
Il numero di ore studiate è mostrato sull’asse x mentre i risultati degli esami sono mostrati sull’asse y. Possiamo vedere che esiste una relazione lineare tra le due variabili: più ore di studio sono associate a punteggi più alti negli esami.

Per quantificare la relazione tra queste due variabili, possiamo eseguire una semplice regressione lineare.

Passaggio 3: eseguire una semplice regressione lineare.

Sulla barra multifunzione superiore di Excel, vai alla scheda Dati e fai clic su Analisi dati . Se non vedi questa opzione, devi prima installare il software gratuito Analysis ToolPak .

Dopo aver fatto clic su Analisi dati, verrà visualizzata una nuova finestra. Selezionare Regressione e fare clic su OK.

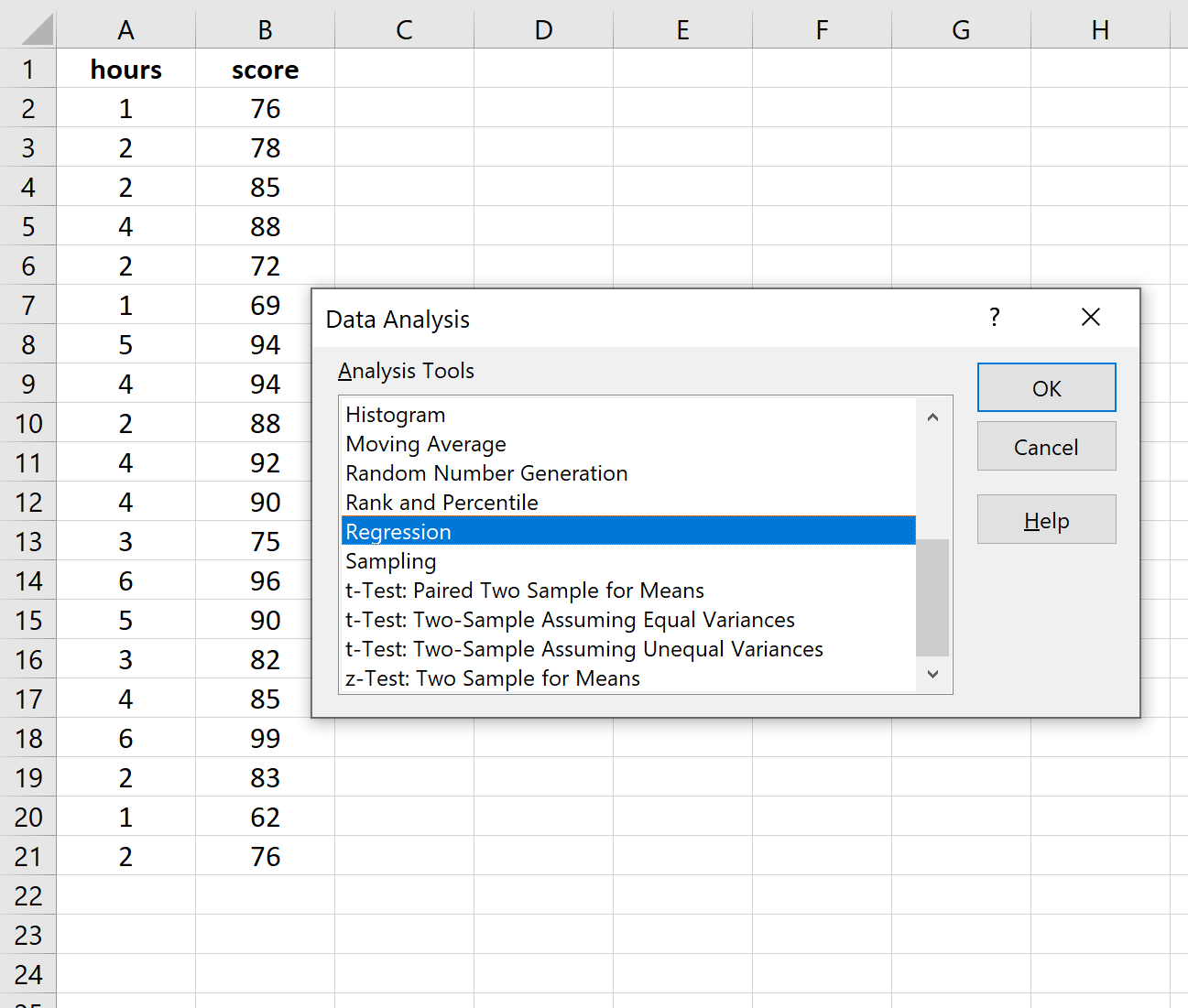
Per Input Y Range , compilare la matrice di valori per la variabile di risposta. Per Input X Range , compilare l’array di valori per la variabile esplicativa.

Seleziona la casella accanto a Etichette per far sapere a Excel che abbiamo incluso i nomi delle variabili negli intervalli di input.

Per Intervallo di output , seleziona una cella in cui desideri che venga visualizzato l’output della regressione.

Quindi fare clic su OK .

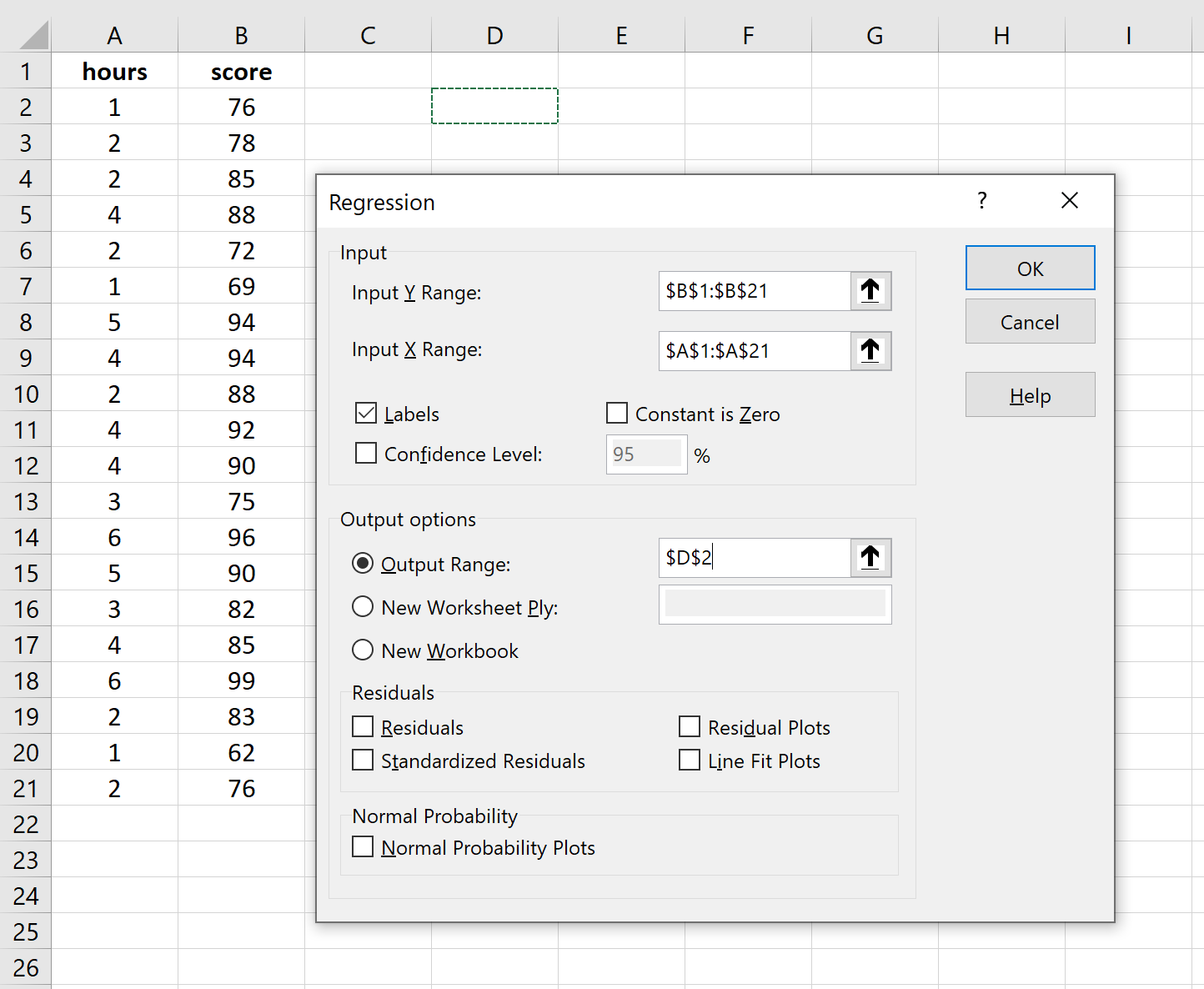
Verrà visualizzato automaticamente il seguente output:

Passaggio 4: interpretare il risultato.

Ecco come interpretare i numeri più rilevanti nel risultato:

R quadrato: 0,7273 . Questo è chiamato coefficiente di determinazione. È la proporzione della varianza nella variabile di risposta che può essere spiegata dalla variabile esplicativa. In questo esempio, il 72,73% della variazione dei punteggi degli esami è spiegata dal numero di ore studiate.

Errore standard: 5.2805 . Questa è la distanza media tra i valori osservati e la retta di regressione. In questo esempio i valori osservati si discostano in media di 5.2805 unità dalla retta di regressione.

F:47.9952 . Questa è la statistica F complessiva per il modello di regressione, calcolata come MS di regressione/MS residuo.

Significato F: 0.0000 . Questo è il valore p associato alla statistica F complessiva. Questo ci dice se il modello di regressione è statisticamente significativo o meno. In altre parole, ci dice se la variabile esplicativa ha un’associazione statisticamente significativa con la variabile di risposta. In questo caso il p-value è inferiore a 0,05, indicando che esiste un’associazione statisticamente significativa tra le ore studiate e il voto ottenuto all’esame.

Coefficienti: i coefficienti ci forniscono i numeri necessari per scrivere l’equazione di regressione stimata. In questo esempio, l’equazione di regressione stimata è:

punteggio esame = 67,16 + 5,2503*(ore)

Interpretiamo il coefficiente di ore nel senso che per ogni ora aggiuntiva studiata, il punteggio dell’esame dovrebbe aumentare in media di 5,2503 . Interpretiamo il coefficiente dell’intercetta nel senso che il punteggio atteso dell’esame per uno studente che studia zero ore è 67,16 .

Possiamo utilizzare questa equazione di regressione stimata per calcolare il punteggio atteso dell’esame per uno studente, in base al numero di ore di studio.

Ad esempio, uno studente che studia per tre ore dovrebbe ottenere un punteggio d’esame di 82,91 :

punteggio esame = 67,16 + 5,2503*(3) = 82,91

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in Excel:

Come creare un grafico residuo in Excel
Come costruire un intervallo di previsione in Excel
Come creare un grafico QQ in Excel