Come eseguire una regressione lineare semplice in python (passo dopo passo)

La regressione lineare semplice è una tecnica che possiamo utilizzare per comprendere la relazione tra una singola variabile esplicativa e una singola variabile di risposta .

Questa tecnica trova la linea che meglio “si adatta” ai dati e assume la forma seguente:

ŷ = b ₀ + b ₁ x

Oro:

• ŷ : il valore di risposta stimato
• b ₀ : L’origine della retta di regressione
• b ₁ : La pendenza della retta di regressione

Questa equazione può aiutarci a comprendere la relazione tra la variabile esplicativa e la variabile di risposta e (supponendo che sia statisticamente significativa) può essere utilizzata per prevedere il valore di una variabile di risposta dato il valore della variabile esplicativa.

Questo tutorial fornisce una spiegazione passo passo su come eseguire una semplice regressione lineare in Python.

Passaggio 1: caricare i dati

Per questo esempio, creeremo un set di dati falso contenente le seguenti due variabili per 15 studenti:

• Numero totale di ore studiate per determinati esami
• Risultato dell’esame

Cercheremo di adattare un semplice modello di regressione lineare utilizzando le ore come variabile esplicativa e i risultati dell’esame come variabile di risposta.

Il codice seguente mostra come creare questo set di dati falso in Python:

 import pandas as pd

#create dataset
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})
      

#view first six rows of dataset
df[0:6]

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81

Passaggio 2: visualizzare i dati

Prima di adattare un semplice modello di regressione lineare, dobbiamo prima visualizzare i dati per comprenderli.

Innanzitutto, vogliamo garantire che la relazione tra ore e punteggio sia approssimativamente lineare, poiché questo è un presupposto di base della semplice regressione lineare.

Possiamo creare un semplice grafico a dispersione per visualizzare la relazione tra le due variabili:

 import matplotlib.pyplot as plt

plt. scatter (df.hours, df.score)
plt. title (' Hours studied vs. Exam Score ')
plt. xlabel (' Hours ')
plt. ylabel (' Score ')
plt. show ()

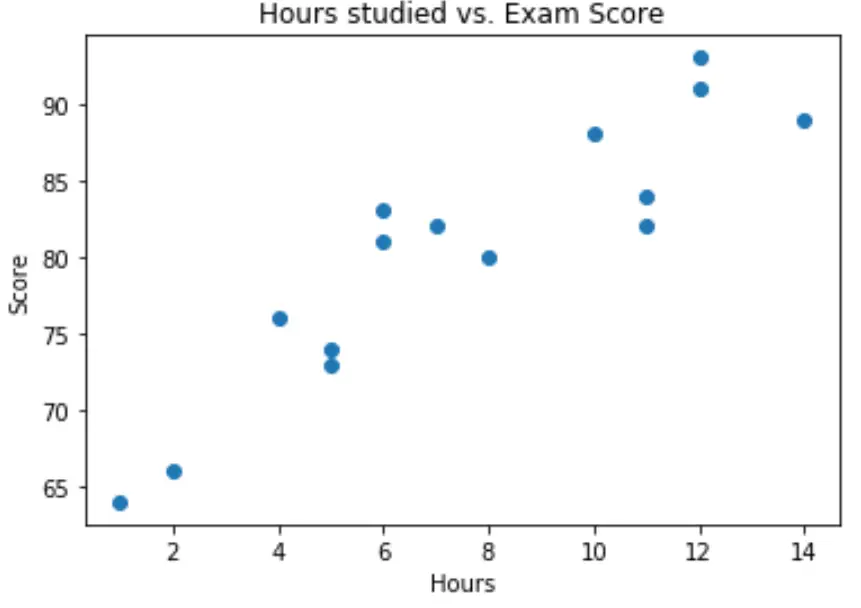
Dal grafico possiamo vedere che la relazione appare lineare. All’aumentare del numero di ore , anche il punteggio tende ad aumentare in modo lineare.

Quindi possiamo creare un boxplot per visualizzare la distribuzione dei risultati dell’esame e verificare la presenza di valori anomali . Per impostazione predefinita, Python definisce un’osservazione come un valore anomalo se è 1,5 volte l’intervallo interquartile sopra il terzo quartile (Q3) o 1,5 volte l’intervallo interquartile sotto il primo quartile (Q1).

Se un’osservazione è anomala, nel boxplot apparirà un piccolo cerchio:

 df. boxplot (column=[' score ']) 

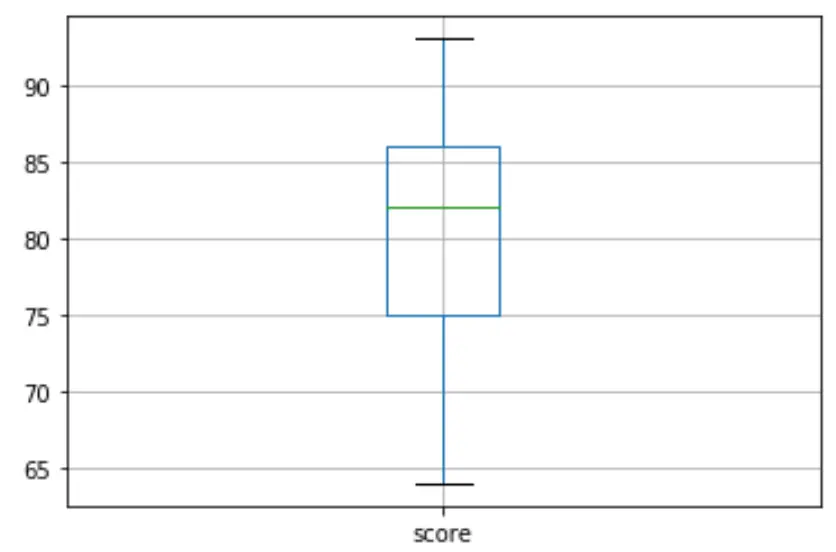
Non ci sono piccoli cerchi nel boxplot, il che significa che non ci sono valori anomali nel nostro set di dati.

Passaggio 3: eseguire una regressione lineare semplice

Una volta confermato che la relazione tra le nostre variabili è lineare e non ci sono valori anomali, possiamo procedere con l’adattamento di un semplice modello di regressione lineare utilizzando le ore come variabile esplicativa e il punteggio come variabile di risposta:

Nota: utilizzeremo la funzione OLS() dalla libreria statsmodels per adattare il modello di regressione.

 import statsmodels.api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Mon, 26 Oct 2020 Prob (F-statistic): 2.25e-06
Time: 15:51:45 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

Dal riepilogo del modello, possiamo vedere che l’equazione di regressione adattata è:

Punteggio = 65.334 + 1.9824*(ore)

Ciò significa che ogni ora aggiuntiva studiata è associata ad un aumento del punteggio medio dell’esame di 1,9824 punti. E il valore originale di 65.334 ci dice il punteggio medio previsto per l’esame per uno studente che studia per zero ore.

Possiamo anche utilizzare questa equazione per trovare il punteggio atteso dell’esame in base al numero di ore di studio di uno studente. Ad esempio, uno studente che studia per 10 ore dovrebbe ottenere un punteggio d’esame di 85.158 :

Punteggio = 65.334 + 1.9824*(10) = 85.158

Ecco come interpretare il resto del riepilogo del modello:

• P>|t| : Questo è il valore p associato ai coefficienti del modello. Poiché il valore p delle ore (0,000) è significativamente inferiore a 0,05, possiamo affermare che esiste un’associazione statisticamente significativa tra ore e punteggio .
• R quadrato: questo numero ci dice che la percentuale di variazione nei punteggi degli esami può essere spiegata dal numero di ore studiate. In generale, maggiore è il valore R quadrato di un modello di regressione, migliore è la capacità delle variabili esplicative di predire il valore della variabile di risposta. In questo caso, l’83,1% della variazione dei punteggi è spiegata dalle ore studiate.
• Statistica F e valore p: la statistica F ( 63,91 ) e il corrispondente valore p ( 2,25e-06 ) ci dicono il significato complessivo del modello di regressione, ovvero se le variabili esplicative nel modello sono utili per spiegare la variazione . nella variabile di risposta. Poiché il valore p in questo esempio è inferiore a 0,05, il nostro modello è statisticamente significativo e le ore sono considerate utili per spiegare la variazione del punteggio .

Passaggio 4: creare grafici residui

Dopo aver adattato il modello di regressione lineare semplice ai dati, il passaggio finale consiste nel creare grafici dei residui.

Uno dei presupposti chiave della regressione lineare è che i residui di un modello di regressione siano distribuiti approssimativamente normalmente e siano omoschedastici a ciascun livello della variabile esplicativa. Se queste ipotesi non vengono soddisfatte, i risultati del nostro modello di regressione potrebbero essere fuorvianti o inaffidabili.

Per verificare che queste ipotesi siano soddisfatte, possiamo creare i seguenti grafici residui:

Grafico dei residui rispetto ai valori adattati: questo grafico è utile per confermare l’omoschedasticità. L’asse x mostra i valori adattati e l’asse y mostra i residui. Finché i residui appaiono distribuiti in modo casuale e uniforme in tutto il grafico attorno al valore zero, possiamo supporre che l’omoschedasticità non sia violata:

 #define figure size
fig = plt. figure (figsize=(12.8))

#produce residual plots
fig = sm.graphics. plot_regress_exog (model, ' hours ', fig=fig)

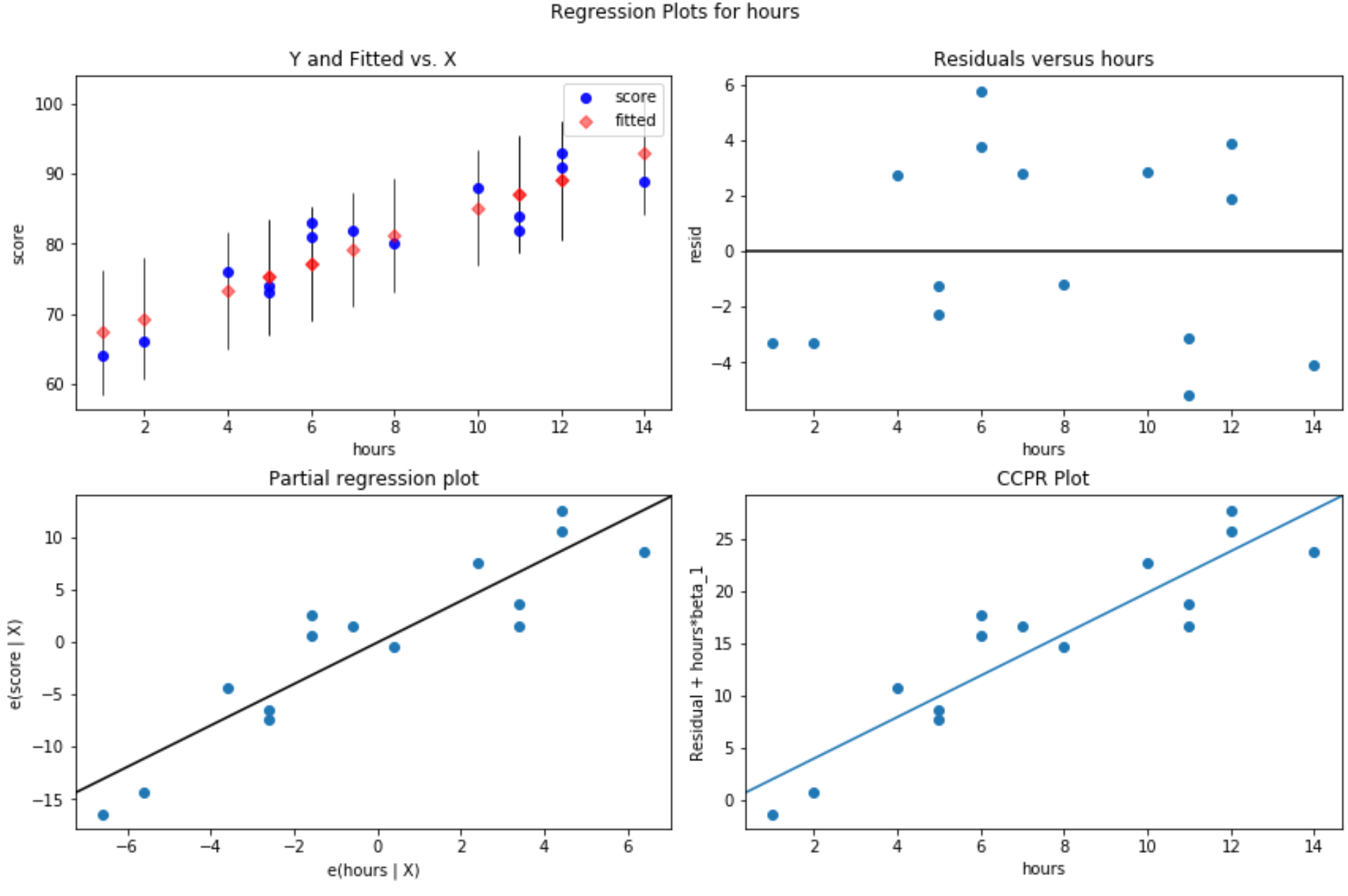
Vengono prodotti quattro appezzamenti. Quello nell’angolo in alto a destra è la trama residua rispetto alla trama modificata. L’asse x su questo grafico mostra i valori effettivi dei punti della variabile predittore e l’asse y mostra il residuo per quel valore.

Poiché i residui sembrano essere sparsi in modo casuale attorno allo zero, ciò indica che l’eteroschedasticità non è un problema con la variabile esplicativa.

Grafico QQ: questo grafico è utile per determinare se i residui seguono una distribuzione normale. Se i valori dei dati nel grafico seguono una linea approssimativamente retta con un angolo di 45 gradi, i dati vengono distribuiti normalmente:

 #define residuals
res = model. reside

#create QQ plot
fig = sm. qqplot (res, fit= True , line=" 45 ")
plt.show() 

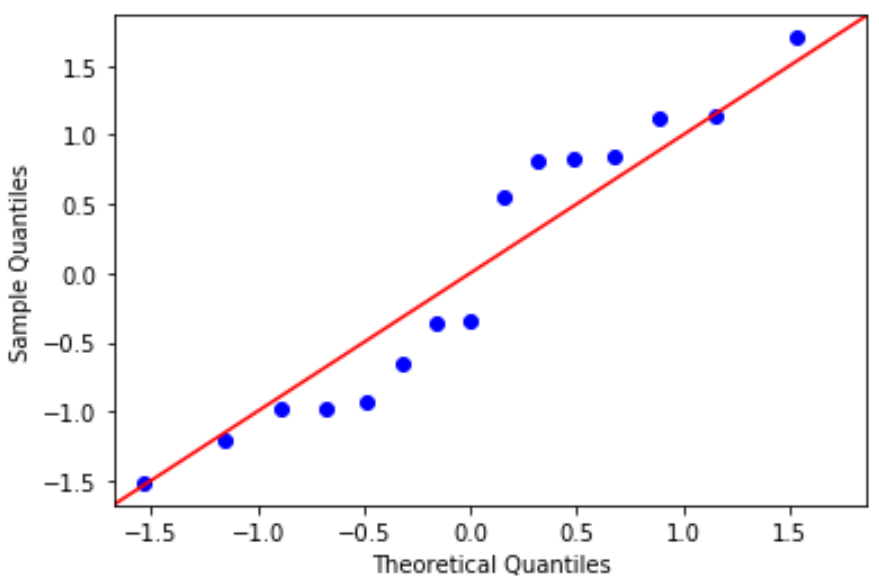
I residui si discostano leggermente dalla linea dei 45 gradi, ma non abbastanza da destare seria preoccupazione. Possiamo supporre che il presupposto di normalità sia soddisfatto.

Poiché i residui sono normalmente distribuiti e omoschedastici, abbiamo verificato che le ipotesi del modello di regressione lineare semplice siano soddisfatte. Pertanto, l’output del nostro modello è affidabile.

Il codice Python completo utilizzato in questo tutorial può essere trovato qui .