Come eseguire una regressione lineare semplice in sas

La regressione lineare semplice è una tecnica che possiamo utilizzare per comprendere la relazione tra una variabile predittore e una variabile di risposta .

Questa tecnica trova la linea che meglio “si adatta” ai dati e assume la forma seguente:

ŷ = b ₀ + b ₁ x

Oro:

• ŷ : il valore di risposta stimato
• b ₀ : L’origine della retta di regressione
• b ₁ : La pendenza della retta di regressione

Questa equazione ci aiuta a comprendere la relazione tra la variabile predittore e la variabile risposta.

Il seguente esempio passo passo mostra come eseguire una semplice regressione lineare in SAS.

Passaggio 1: creare i dati

Per questo esempio, creeremo un set di dati contenente il numero totale di ore studiate e il voto dell’esame finale di 15 studenti.

Adatteremo un semplice modello di regressione lineare utilizzando le ore come variabile predittiva e il punteggio come variabile di risposta.

Il codice seguente mostra come creare questo set di dati in SAS:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

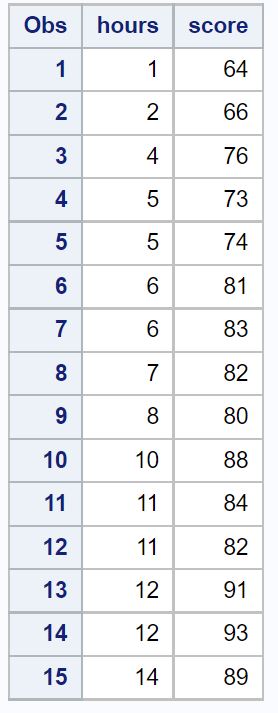
Passaggio 2: adattare il modello di regressione lineare semplice

Successivamente, utilizzeremo proc reg per adattare il modello di regressione lineare semplice:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

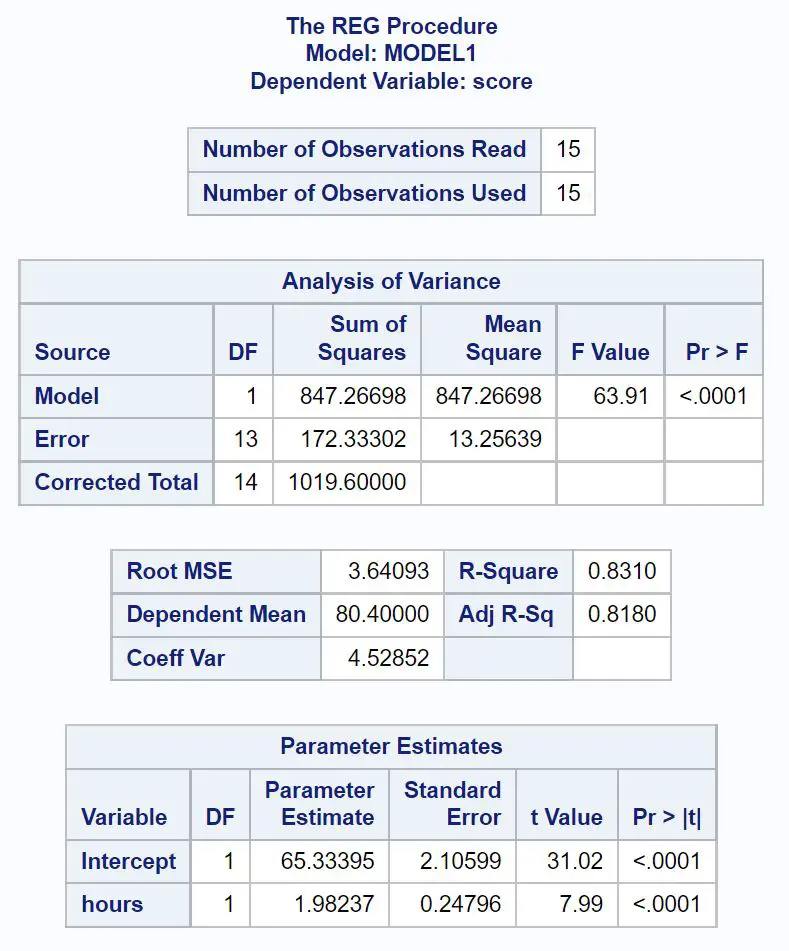
Ecco come interpretare i valori più importanti di ciascuna tabella nel risultato:

Tabella di analisi degli scostamenti:

Il valore F complessivo del modello di regressione è 63,91 e il valore p corrispondente è <0,0001 .

Poiché questo valore p è inferiore a 0,05, concludiamo che il modello di regressione nel suo insieme è statisticamente significativo. In altre parole, le ore sono una variabile utile per prevedere i risultati degli esami.

Tabella di adattamento del modello:

Il valore R-Square ci dice la percentuale di variazione nei punteggi degli esami che può essere spiegata dal numero di ore studiate.

In generale, maggiore è il valore R quadrato di un modello di regressione, migliore è la capacità delle variabili predittive di prevedere il valore della variabile di risposta.

In questo caso, l’ 83,1% della variazione dei punteggi degli esami è spiegabile con il numero di ore studiate. Questo valore è piuttosto elevato, indicando che le ore studiate sono una variabile molto utile per prevedere i risultati degli esami.

Tabella delle stime dei parametri:

Da questa tabella possiamo vedere l’equazione di regressione adattata:

Punteggio = 65,33 + 1,98*(ore)

Interpretiamo ciò nel senso che ogni ora aggiuntiva studiata è associata a un aumento medio di 1,98 punti nel punteggio dell’esame.

Il valore originale ci dice che il punteggio medio dell’esame per uno studente che studia per zero ore è 65,33 .

Possiamo anche utilizzare questa equazione per trovare il punteggio atteso dell’esame in base al numero di ore di studio di uno studente.

Ad esempio, uno studente che studia per 10 ore dovrebbe ottenere un punteggio d’esame di 85,13 :

Punteggio = 65,33 + 1,98*(10) = 85,13

Poiché in questa tabella il valore p (<0,0001) per le ore è inferiore a 0,05, concludiamo che si tratta di una variabile predittiva statisticamente significativa.

Passaggio 3: analizzare i grafici residui

La regressione lineare semplice fa due importanti ipotesi sui residui del modello:

• I residui sono distribuiti normalmente.
• I residui hanno la stessa varianza (” omoschedasticità “) a ciascun livello della variabile predittrice.

Se queste ipotesi non vengono soddisfatte, i risultati del nostro modello di regressione potrebbero non essere affidabili.

Per verificare che queste ipotesi siano soddisfatte, possiamo analizzare i grafici residui che SAS visualizza automaticamente nell’output:

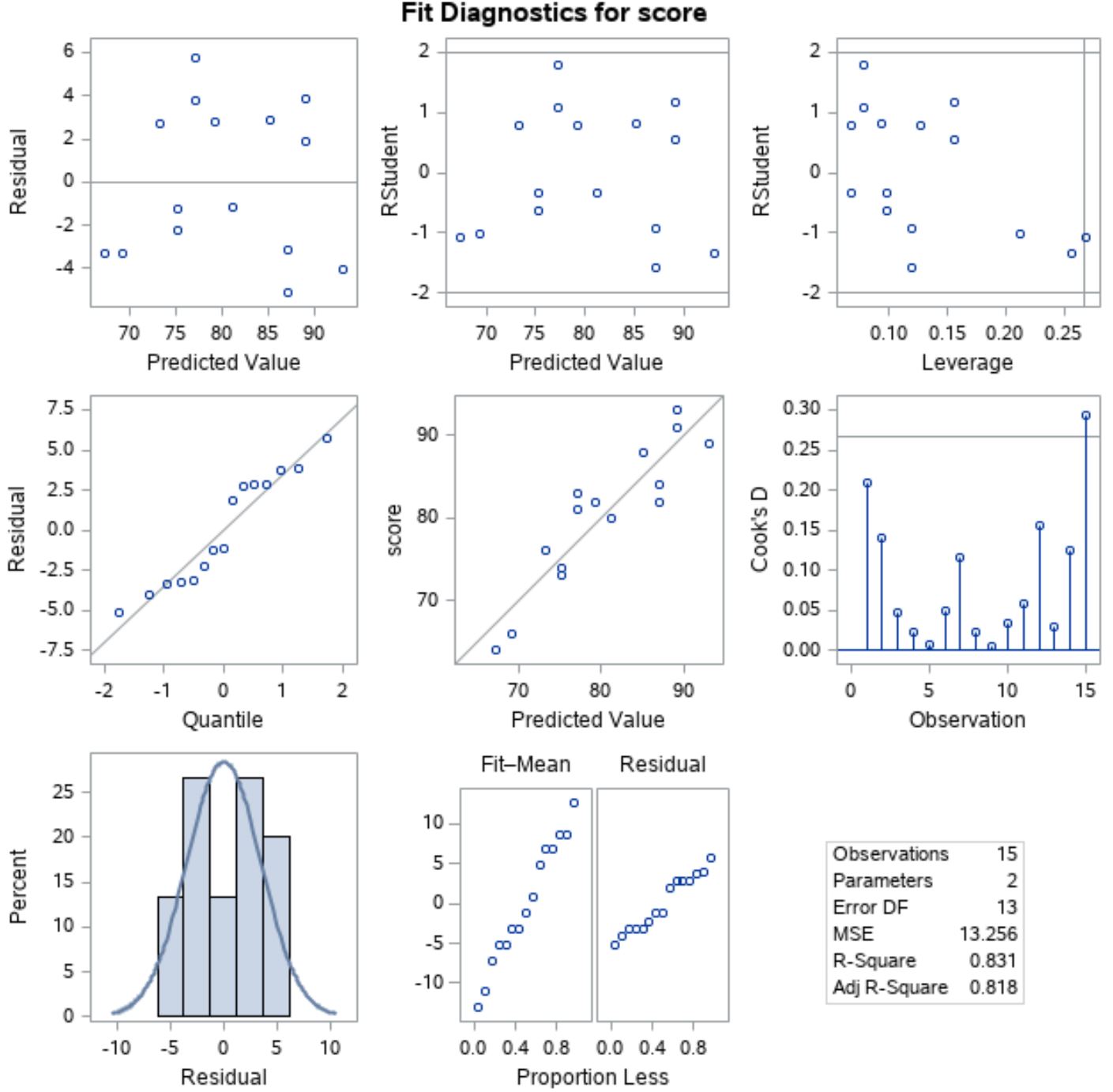
Per verificare che i residui siano distribuiti normalmente , possiamo analizzare il grafico nella posizione sinistra della linea mediana con “Quantile” lungo l’asse x e “Residuo” lungo l’asse y.

Questo grafico è chiamato grafico QQ , abbreviazione di “quantile-quantile”, e viene utilizzato per determinare se i dati sono distribuiti normalmente o meno. Se i dati sono distribuiti normalmente, i punti su un grafico QQ giacciono su una linea diagonale retta.

Dal grafico possiamo vedere che i punti giacciono all’incirca lungo una linea retta diagonale, quindi possiamo supporre che i residui siano distribuiti normalmente.

Successivamente, per verificare che i residui siano omoschedastici , possiamo guardare il grafico nella posizione sinistra della prima riga con “Valore previsto” lungo l’asse x e “Residuo” lungo l’asse y.

Se i punti della trama sono sparsi in modo casuale attorno allo zero senza uno schema chiaro, allora possiamo supporre che i residui siano omoschedastici.

Dal grafico possiamo vedere che i punti sono sparsi attorno allo zero in modo casuale con una varianza approssimativamente uguale ad ogni livello in tutto il grafico, quindi possiamo assumere che i residui siano omoschedastici.

Poiché entrambe le ipotesi sono soddisfatte, possiamo supporre che i risultati del modello di regressione lineare semplice siano affidabili.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in SAS:

Come eseguire ANOVA unidirezionale in SAS
Come eseguire ANOVA bidirezionale in SAS
Come calcolare la correlazione in SAS