Regressione logaritmica in r (passo dopo passo)

La regressione logaritmica è un tipo di regressione utilizzato per modellare situazioni in cui la crescita o il declino accelerano rapidamente all’inizio e poi rallentano nel tempo.

Ad esempio, il grafico seguente mostra un esempio di decadimento logaritmico:

Per questo tipo di situazione, la relazione tra una variabile predittrice e una variabile di risposta potrebbe essere ben modellata utilizzando la regressione logaritmica.

L’equazione per un modello di regressione logaritmica assume la forma seguente:

y = a + b*ln(x)

Oro:

• y: la variabile di risposta
• x: la variabile predittiva
• a, b: i coefficienti di regressione che descrivono la relazione tra x e y

Il seguente esempio passo passo mostra come eseguire la regressione logaritmica in R.

Passaggio 1: creare i dati

Innanzitutto, creiamo dati falsi per due variabili: x e y :

 x=1:15

y=c(59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5)

Passaggio 2: visualizzare i dati

Successivamente, creiamo un rapido grafico a dispersione per visualizzare la relazione tra x e y :

 plot(x, y) 

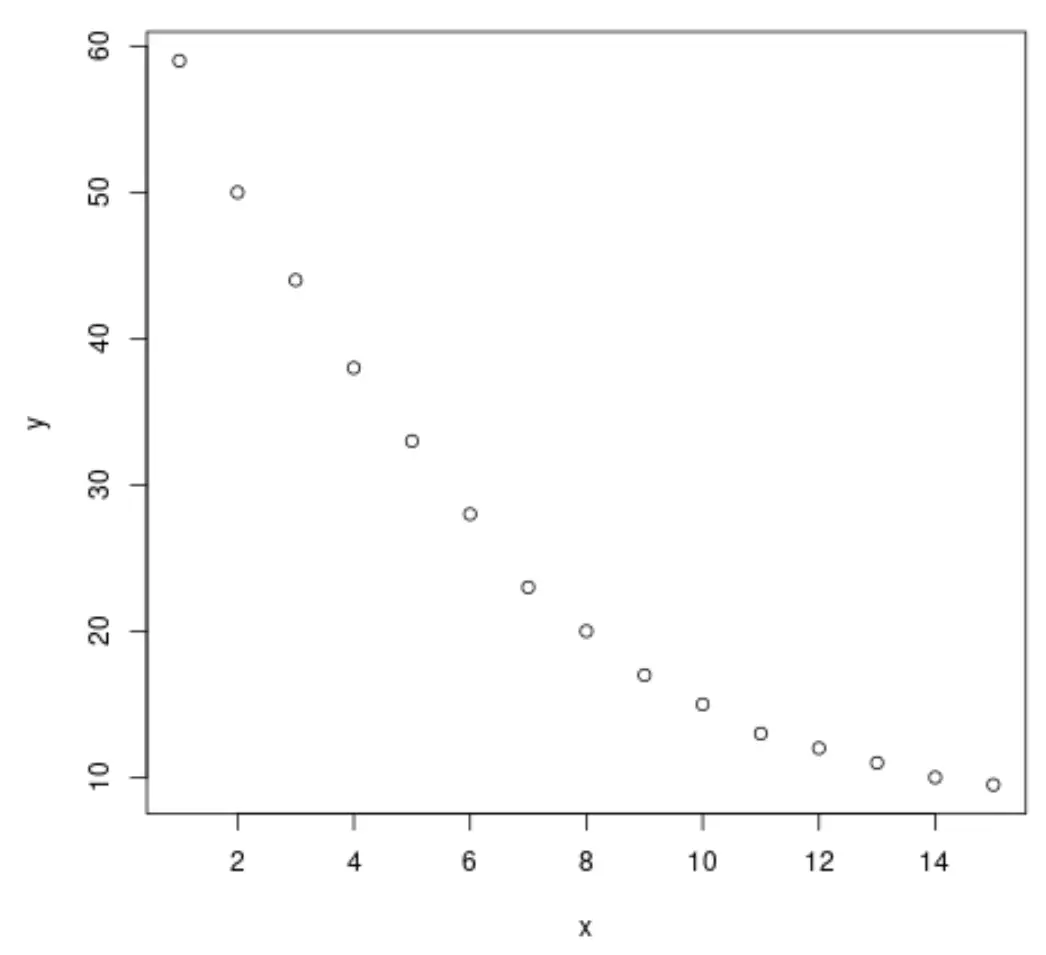
Dal grafico possiamo vedere che esiste un chiaro modello di decadimento logaritmico tra le due variabili. Il valore della variabile di risposta, y , inizialmente diminuisce rapidamente, quindi rallenta nel tempo.

Sembra quindi saggio adattare un’equazione di regressione logaritmica per descrivere la relazione tra le variabili.

Passaggio 3: adattare il modello di regressione logaritmica

Successivamente utilizzeremo la funzione lm() per adattare un modello di regressione logaritmica, utilizzando il logaritmo naturale di x come variabile predittrice e y come variabile di risposta.

 #fit the model
model <- lm(y ~ log (x))

#view the output of the model
summary(model)

Call:
lm(formula = y ~ log(x))

Residuals:
   Min 1Q Median 3Q Max 
-4.069 -1.313 -0.260 1.127 3.122 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.0686 1.4090 44.76 1.25e-15 ***
log(x) -20.1987 0.7019 -28.78 3.70e-13 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.054 on 13 degrees of freedom
Multiple R-squared: 0.9845, Adjusted R-squared: 0.9834 
F-statistic: 828.2 on 1 and 13 DF, p-value: 3.702e-13

Il valore F complessivo del modello è 828,2 e il valore p corrispondente è estremamente basso (3,702e-13), indicando che il modello nel suo insieme è utile.

Utilizzando i coefficienti della tabella di output, possiamo vedere che l’equazione di regressione logaritmica adattata è:

y = 63,0686 – 20,1987 * ln(x)

Possiamo utilizzare questa equazione per prevedere la variabile di risposta, y , in base al valore della variabile predittrice, x . Ad esempio, se x = 12, allora prevediamo che y sarebbe 12,87 :

y = 63,0686 – 20,1987 * ln(12) = 12,87

Bonus: sentiti libero di utilizzare questo calcolatore di regressione logaritmica online per calcolare automaticamente l’equazione di regressione logaritmica per un determinato predittore e variabile di risposta.

Passaggio 4: Visualizza il modello di regressione logaritmica

Infine, possiamo creare un rapido grafico per visualizzare quanto bene il modello di regressione logaritmica si adatta ai dati:

 #plot x vs. y
plot(x, y)

#define x-values to use for regression line
x=seq(from= 1 , to= 15 , length. out = 1000 )

#use the model to predict the y-values based on the x-values
y=predict(model,newdata=list(x=seq(from= 1 ,to= 15 ,length. out = 1000 )),
          interval=" confidence ")

#add the fitted regression line to the plot (lwd specifies the width of the line)
matlines(x,y, lwd= 2 )

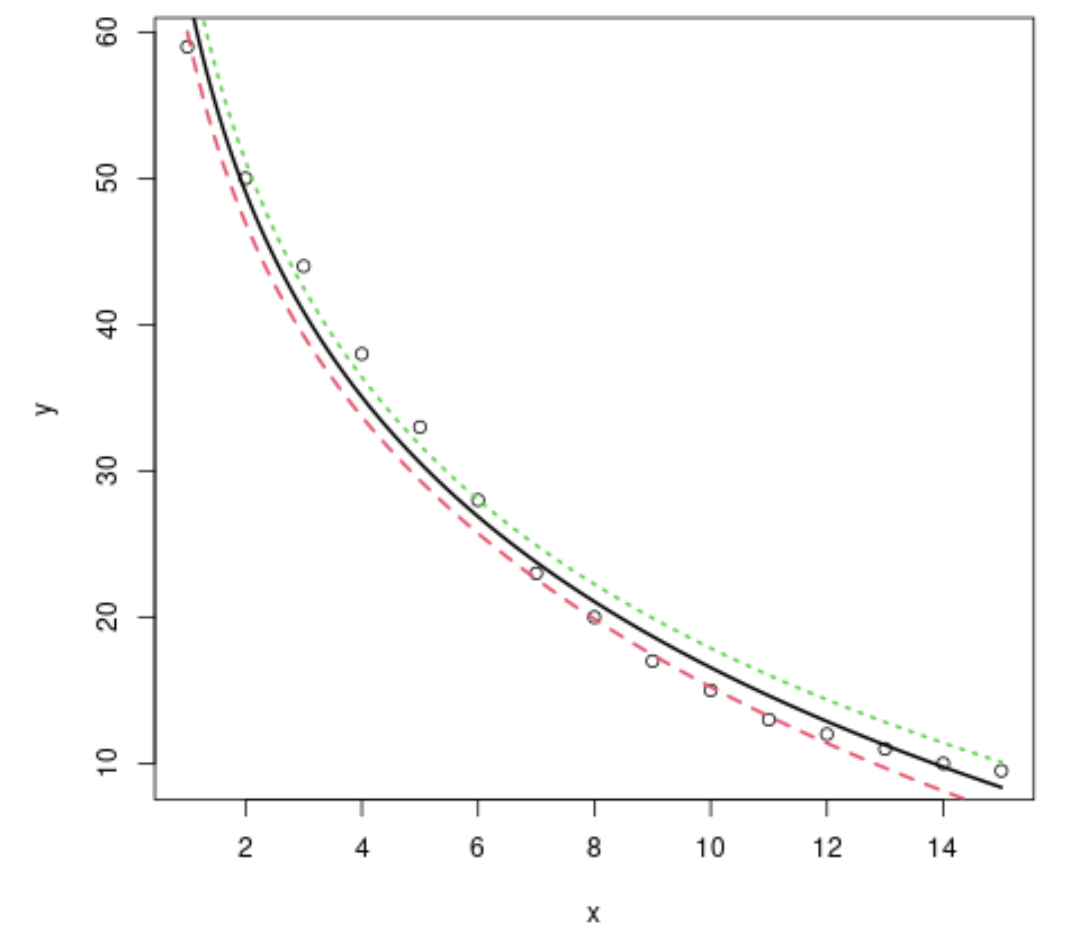
Possiamo vedere che il modello di regressione logaritmica fa un buon lavoro nell’adattare questo particolare set di dati.

Risorse addizionali

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come eseguire la regressione quadratica in R
Come eseguire la regressione esponenziale in R
Come eseguire la regressione polinomiale in R