Come eseguire la regressione logistica in sas

La regressione logistica è un metodo che possiamo utilizzare per adattare un modello di regressione quando la variabile di risposta è binaria.

La regressione logistica utilizza un metodo noto come stima di massima verosimiglianza per trovare un’equazione della seguente forma:

log[p(X) / (1 _– p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Oro:

• X _j : la j- ^esima variabile predittiva
• β _j : stima del coefficiente per la j ^-esima variabile predittiva

La formula sul lato destro dell’equazione prevede le probabilità logaritmiche che la variabile di risposta assuma il valore 1.

Il seguente esempio passo passo mostra come adattare un modello di regressione logistica in SAS.

Passaggio 1: crea il set di dati

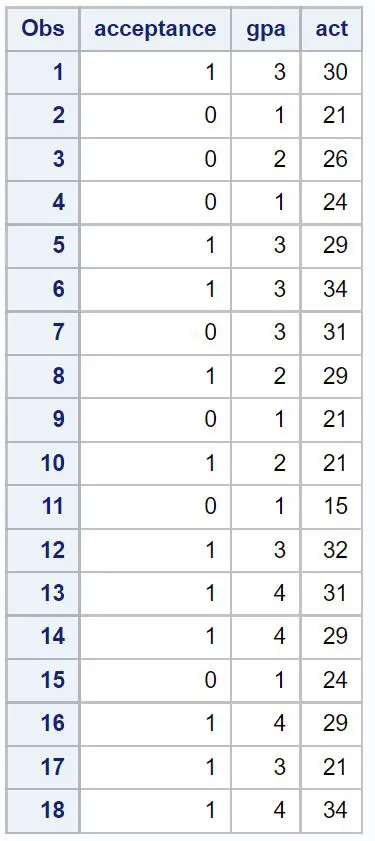
Innanzitutto, creeremo un set di dati contenente informazioni sulle seguenti tre variabili per 18 studenti:

• Accettazione in un determinato college (1 = sì, 0 = no)
• GPA (scala da 1 a 4)
• Punteggio ACT (scala da 1 a 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

Passaggio 2: adattare il modello di regressione logistica

Successivamente, utilizzeremo la logistica di processo per adattare il modello di regressione logistica, utilizzando “accettazione” come variabile di risposta e “gpa” e “agire” come variabili predittive.

Nota : è necessario specificare la diminuzione affinché SAS possa prevedere la probabilità che la variabile di risposta assuma un valore pari a 1. Per impostazione predefinita, SAS prevede la probabilità che la variabile di risposta assuma un valore pari a 0.

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

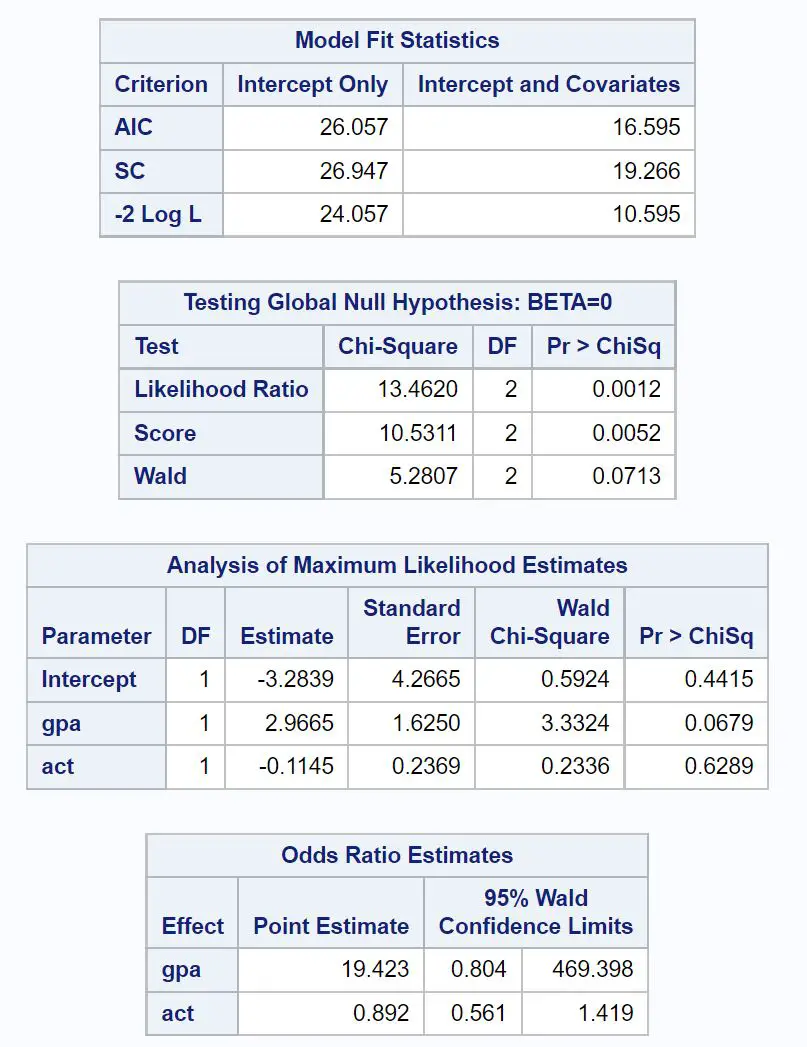
La prima tabella di interesse è intitolata Statistiche di adattamento del modello .

Da questa tabella possiamo vedere il valore AIC del modello, che risulta essere 16.595 . Più basso è il valore AIC, migliore è la capacità del modello di adattare i dati.

Tuttavia, non esiste una soglia per ciò che è considerato un valore AIC “buono” . Utilizziamo piuttosto l’AIC per confrontare l’adattamento di più modelli allo stesso set di dati. Il modello con il valore AIC più basso è generalmente considerato il migliore.

La prossima tabella di interesse è intitolata Test dell’ipotesi nulla globale: BETA=0 .

Da questa tabella, possiamo vedere il valore chi-quadrato del rapporto di verosimiglianza di 13,4620 con un valore p corrispondente di 0,0012 .

Poiché questo valore p è inferiore a 0,05, ciò ci dice che il modello di regressione logistica nel suo insieme è statisticamente significativo.

Successivamente, possiamo analizzare le stime dei coefficienti nella tabella intitolata Analisi delle stime di massima verosimiglianza .

Da questa tabella possiamo vedere i coefficienti per gpa e act, che indicano la variazione media nelle probabilità logaritmiche di essere accettati al college per un aumento di un’unità in ciascuna variabile.

Per esempio:

• Un aumento di un’unità del valore GPA è associato a un aumento medio di 2,9665 nelle probabilità logaritmiche di essere accettato al college.
• Un aumento di un’unità del punteggio ACT è associato a una diminuzione media di 0,1145 nelle probabilità logaritmiche di essere accettato al college.

I corrispondenti valori p nel risultato ci danno anche un’idea di quanto sia efficace ciascuna variabile predittiva nel prevedere la probabilità di essere accettato:

• Valore P GPA: 0,0679
• Valore P ACT: 0,6289

Questo ci dice che il GPA sembra essere un predittore statisticamente significativo dell’accettazione del college, mentre il punteggio ACT non sembra essere statisticamente significativo.

Risorse addizionali

I seguenti tutorial spiegano come adattare altri modelli di regressione in SAS:

Come eseguire una regressione lineare semplice in SAS
Come eseguire la regressione lineare multipla in SAS