Come eseguire la regressione logistica in spss

La regressione logistica è un metodo che utilizziamo per adattare un modello di regressione quando la variabile di risposta è binaria.

Questo tutorial spiega come eseguire la regressione logistica in SPSS.

Esempio: regressione logistica in SPSS

Utilizzare i passaggi seguenti per eseguire la regressione logistica in SPSS per un set di dati che indica se i giocatori di basket universitari sono stati arruolati o meno nell’NBA (draft: 0 = no, 1 = sì) in base al loro GPA. punti per partita e il loro livello di divisione.

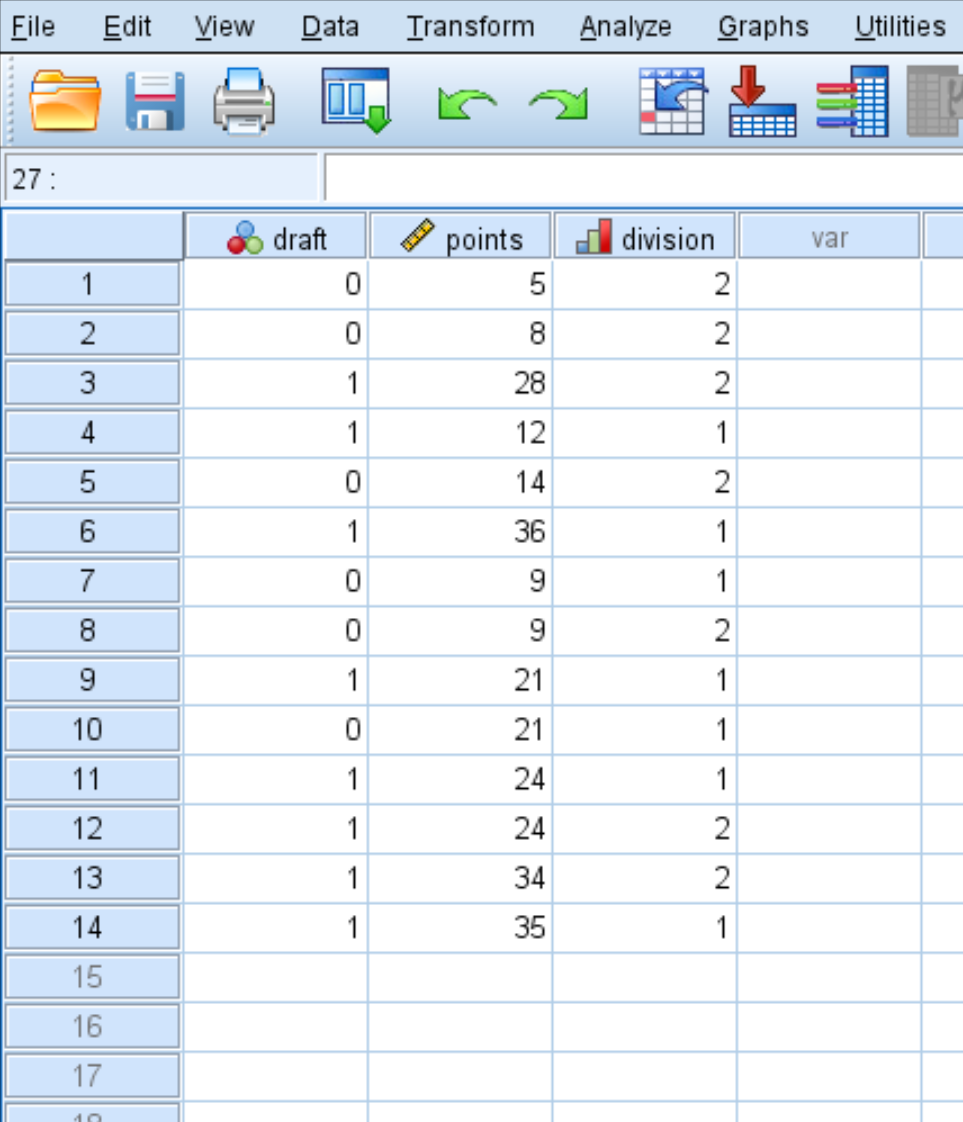
Passaggio 1: inserisci i dati.

Per prima cosa inserisci i seguenti dati:

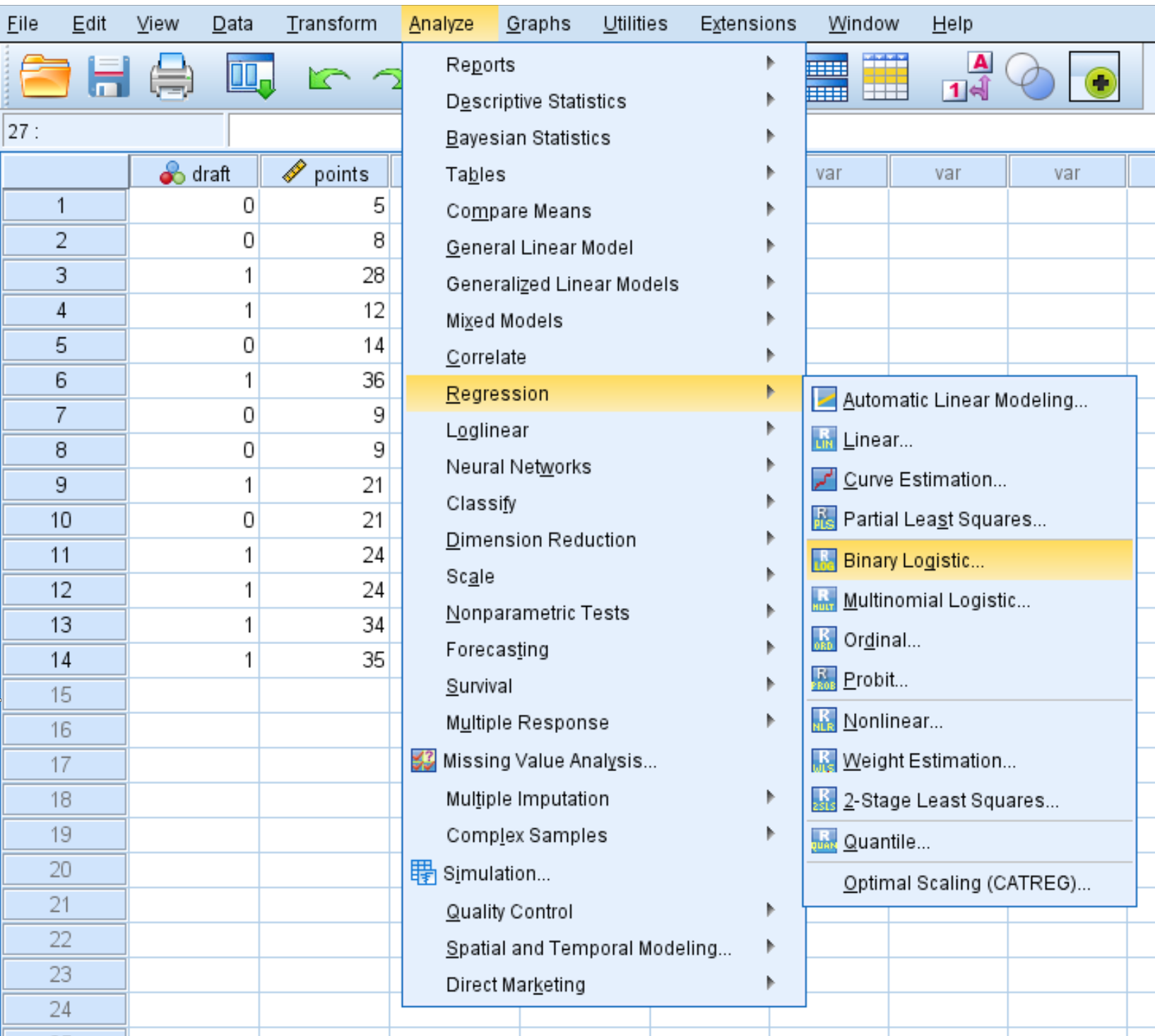
Passaggio 2: eseguire la regressione logistica.

Fare clic sulla scheda Analizza , quindi su Regressione , quindi su Regressione logistica binaria :

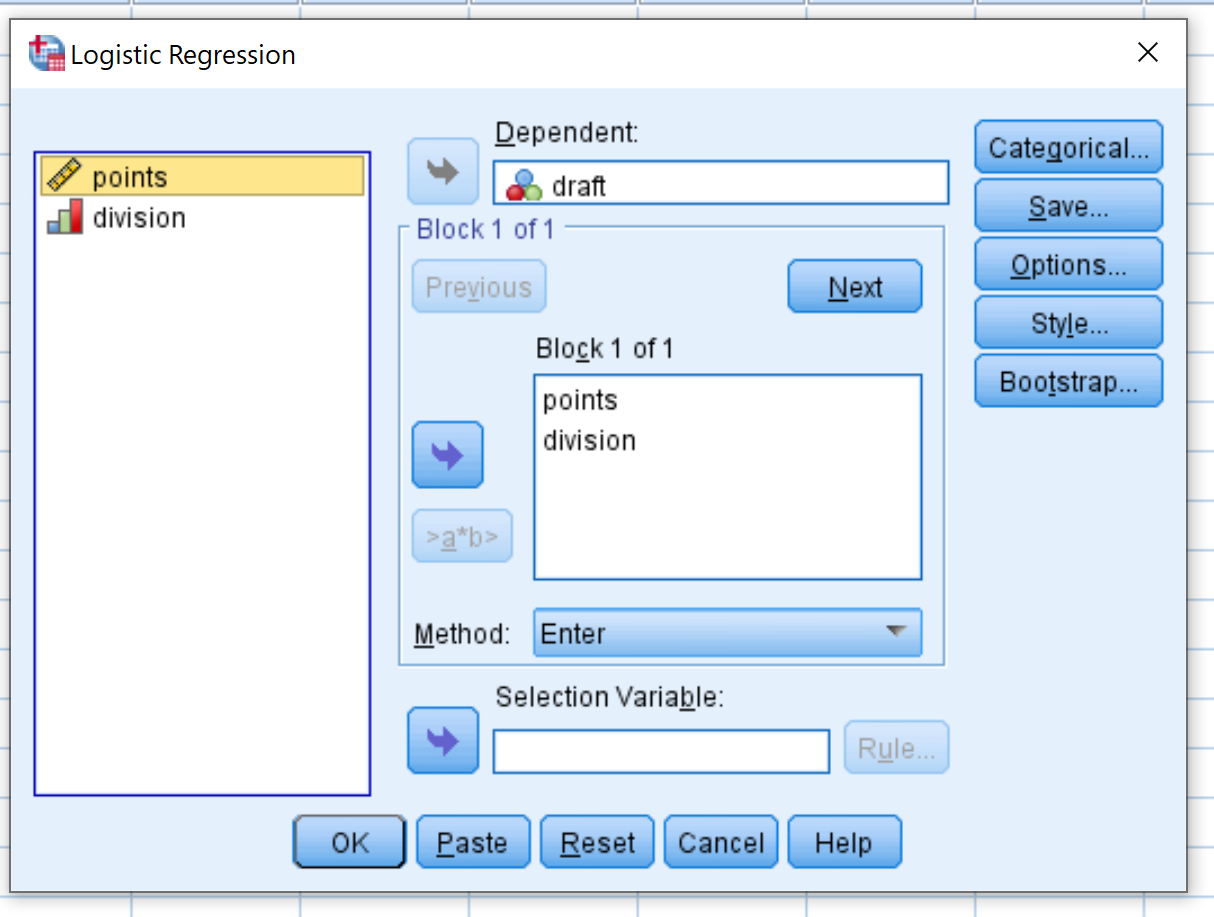
Nella nuova finestra visualizzata, trascina il progetto della variabile di risposta binaria nell’area denominata Dipendente. Quindi trascina i due punti e la divisione delle variabili predittive nella casella denominata Blocco 1 di 1. Lascia il metodo impostato su Invio. Quindi fare clic su OK .

Passaggio 3. Interpretare il risultato.

Dopo aver fatto clic su OK , verrà visualizzato il risultato della regressione logistica:

Ecco come interpretare il risultato:

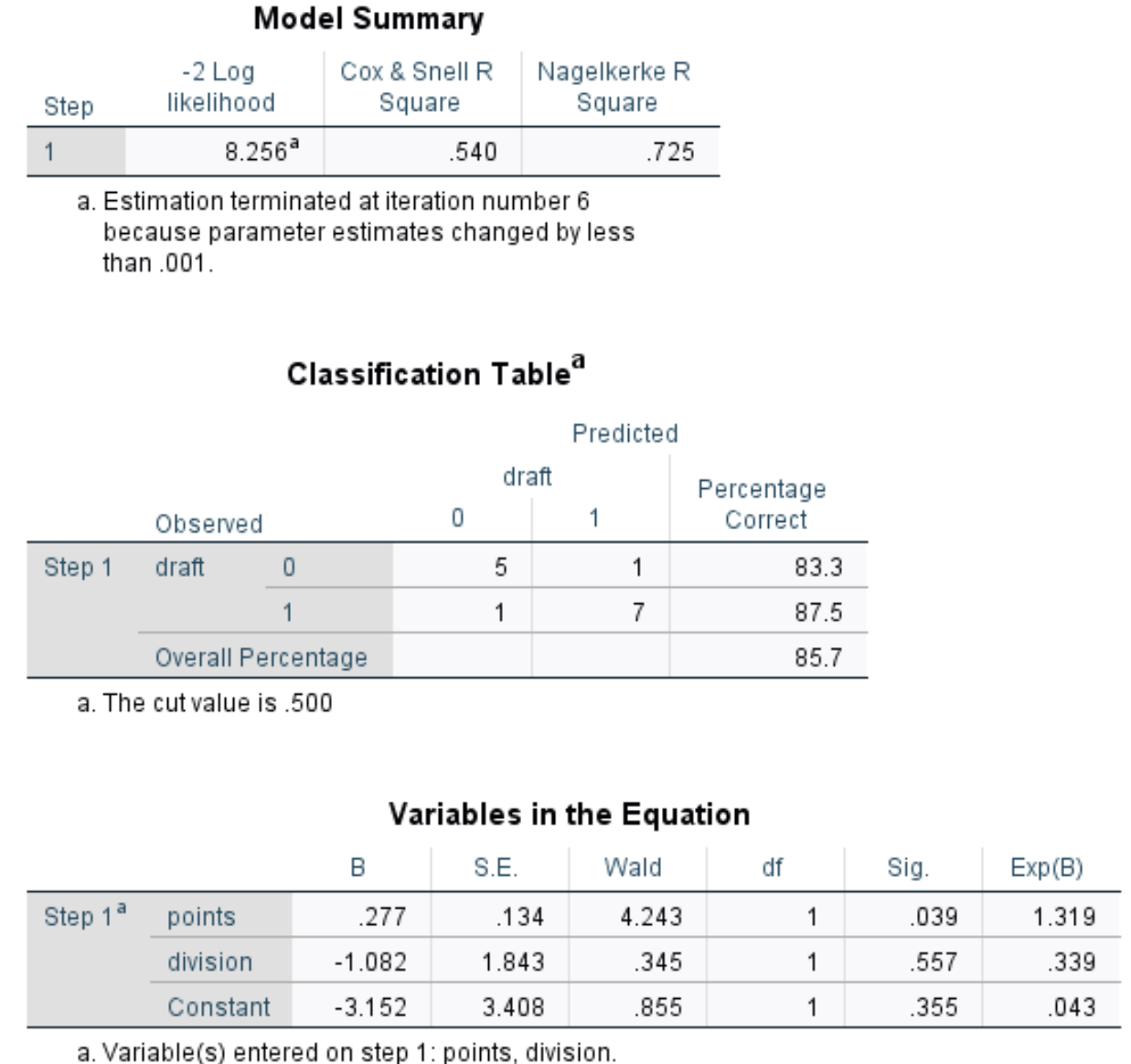
Riepilogo del modello: la metrica più utile in questa tabella è il quadrato R di Nagelkerke, che ci indica la percentuale di variazione nella variabile di risposta che può essere spiegata dalle variabili predittive. In questo caso i punti e la divisione possono spiegare il 72,5% della variabilità del draft.

Tabella di classificazione: la metrica più utile in questa tabella è la percentuale complessiva, che ci indica la percentuale di osservazioni che il modello è stato in grado di classificare correttamente. In questo caso, il modello di regressione logistica è stato in grado di prevedere correttamente l’esito del draft per l’ 85,7% dei giocatori.

Variabili nell’equazione: quest’ultima tabella ci fornisce diverse misurazioni utili, tra cui:

• Wald: statistica del test Wald per ciascuna variabile predittiva, utilizzata per determinare se ciascuna variabile predittiva è statisticamente significativa o meno.
• Sig: il valore p che corrisponde alla statistica del test di Wald per ciascuna variabile predittrice. Vediamo che il valore p per i punti è 0,039 e il valore p per la divisione è 0,557.
• Esp(B): il rapporto odd per ciascuna variabile predittrice. Questo ci dice la variazione delle probabilità che un giocatore venga scelto associato a un aumento di un’unità in una determinata variabile predittiva. Ad esempio, le probabilità che un giocatore della Divisione 2 venga scelto sono solo 0,339 delle probabilità che un giocatore della Divisione 1 venga scelto. Allo stesso modo, ogni aumento unitario aggiuntivo di punti per partita è associato a un aumento di 1.319 delle probabilità che un giocatore venga scelto.

Possiamo quindi utilizzare i coefficienti (i valori nella colonna etichettata B) per prevedere la probabilità che un dato giocatore venga scelto, utilizzando la seguente formula:

Probabilità = e ^{-3.152 + 0.277 (punti) – 1.082 (divisione)} / (1+e ^{-3.152 + 0.277 (punti) – 1.082 (divisione)} )

Ad esempio, la probabilità che un giocatore che ha una media di 20 punti a partita e gioca in Division 1 venga scelto può essere calcolata come segue:

Probabilità = e ^{-3,152 + 0,277(20) – 1,082(1)} / (1+e ^{-3,152 + 0,277(20) – 1,082(1)} ) = 0,787 .

Poiché questa probabilità è maggiore di 0,5, prevediamo che questo giocatore verrà scelto.

Passaggio 4. Riportare i risultati.

Infine, vorremmo riportare i risultati della nostra regressione logistica. Ecco un esempio di come eseguire questa operazione:

È stata eseguita una regressione logistica per determinare in che modo i punti per partita e il livello di divisione influiscono sulla probabilità di un giocatore di basket di essere scelto. Nell’analisi sono stati utilizzati un totale di 14 giocatori.

Il modello ha spiegato il 72,5% della variazione nei risultati del progetto e ha classificato correttamente l’85,7% dei casi.

Le probabilità che un giocatore della Divisione 2 venisse scelto erano solo 0,339 delle probabilità che un giocatore della Divisione 1 venisse scelto.

Ogni aumento unitario aggiuntivo di punti per partita era associato a un aumento di 1.319 nelle probabilità che un giocatore venisse scelto.