Regressione polinomiale

Di Benjamin anderson Agosto 2, 2023 Statistiche 0 commenti

Questo articolo spiega cos’è la regressione polinomiale nelle statistiche e come viene eseguita. Inoltre, potrai vedere un esempio in cui viene eseguita una regressione polinomiale.

Cos’è la regressione polinomiale?

La regressione polinomiale , o regressione polinomiale , è un modello di regressione in cui la relazione tra la variabile indipendente X e la variabile dipendente Y è modellata utilizzando un polinomio.

Ad esempio, l’equazione per un modello di regressione polinomiale quadratica è y=β ₀ +β ₁ x+β ₂ x ² +ε.

La regressione polinomiale è utile per adattare set di dati i cui grafici sono curve polinomiali. Quindi, se il dot plot di un campione di dati ha la forma di una parabola, sarà meglio costruire un modello di regressione quadratica piuttosto che un modello di regressione lineare. In questo modo, l’equazione del modello di regressione si adatterà meglio al campione di dati.

Tieni presente che la regressione polinomiale è un tipo di regressione non lineare, proprio come la regressione esponenziale e la regressione logaritmica.

Formula di regressione polinomiale

L’equazione per un modello di regressione polinomiale è y=β ₀ +β ₁ x+β ₂ x ² +β ₃ x ³ …+β _m x ^m +ε.

$y=\beta_0+\beta_1 x+\beta_2 x^2+\beta_3 x^3+\dots+\beta_m x^m+\varepsilon$

Oro:

$y$

è la variabile dipendente.
$x$

è la variabile indipendente.
$\beta_0$

è la costante dell’equazione di regressione polinomiale.
$\beta_i$

è il coefficiente di regressione associato alla variabile

$x^i$

.
$\bm{\varepsilon}$

Questo è l’errore o residuo, cioè la differenza tra il valore osservato e il valore stimato dal modello.

Quindi, se abbiamo un campione con un totale di

$n$

osservazioni, possiamo proporre il modello di regressione polinomiale in forma matriciale:

$\begin{pmatrix}y_1\\y_2\\y_3\\\vdots\\y_n\end{pmatrix}=\begin{pmatrix}1&x_1&x_1^2&\dots&x_1^m\\1&x_2&x_2^2&\dots&x_2^m\\1&x_3&x_3^2&\dots&x_3^m\\ \vdots&\vdots&\ddots&\vdots\\1&x_{n}&x_n^2&\dots&x_n^m\end{pmatrix}\cdot\begin{pmatrix}\beta_0\\\beta_1\\\beta_2\\\vdots\\\beta_m\end{pmatrix}+\begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\varepsilon_3\\\vdots\\\varepsilon_n\end{pmatrix}$

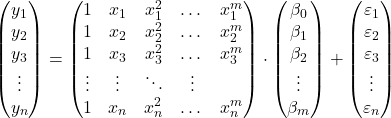
L’espressione della matrice sopra può essere riscritta assegnando una lettera a ciascuna matrice:

$Y=X\beta+\varepsilon$

Pertanto, applicando il criterio dei minimi quadrati , possiamo arrivare alla formula per la stima dei coefficienti di un modello di regressione polinomiale :

$\widehat{\beta}=\left(X^tX\right)^{-1}X^tY$

Tuttavia, eseguire questi calcoli manualmente è molto laborioso e richiede molto tempo, quindi è più conveniente utilizzare un software per computer (come Minitab o Excel) che consente di eseguire un modello di regressione polinomiale molto più velocemente.

Esempio di modello di regressione polinomiale

Ora che conosciamo la definizione di regressione polinomiale e come viene eseguita, diamo un’occhiata a un esempio di vita reale per comprendere appieno il concetto.

Innanzitutto va tenuto presente che un modello di regressione polinomiale dovrebbe essere eseguito quando il grafico dei dati ha la forma di una curva polinomiale. Ad esempio, se il dotplot ha la forma di una curva cubica, dobbiamo costruire un modello di regressione polinomiale di terzo grado.

Quindi, come puoi vedere nell’immagine seguente, il dot plot dei nostri dati ha una forma quadratica, perché aumentando il valore della variabile indipendente, la variabile dipendente cresce più velocemente. In questo caso è stato eseguito un modello di regressione lineare e come puoi vedere non adatta bene i punti perché ha sezioni in cui la linea è sotto tutti i punti e sezioni in cui la linea è sopra di essi.

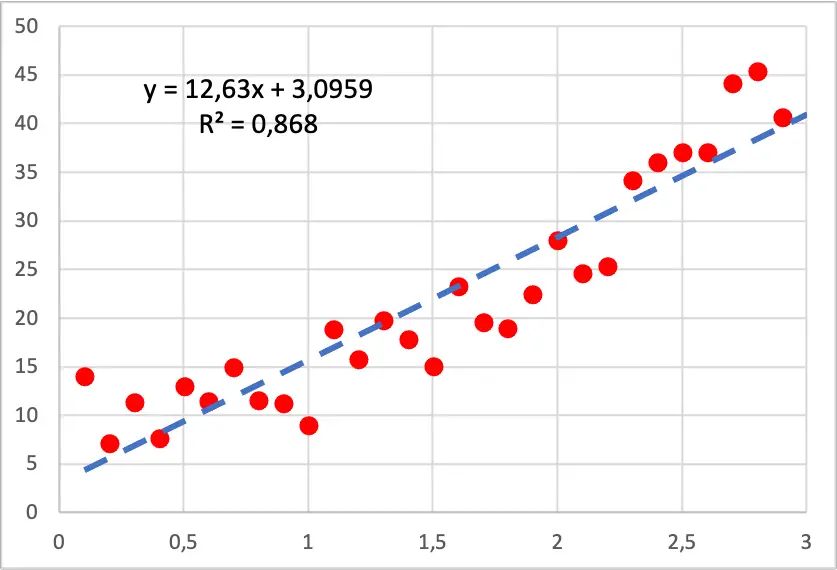
D’altra parte, se eseguiamo un modello di regressione polinomiale quadratica, si adatta molto meglio ai dati del campione, come puoi vedere nell’immagine qui sotto.

Inoltre, quando si sviluppa un modello di regressione polinomiale, il coefficiente di determinazione migliora notevolmente poiché passa dall’86,80% al 94,05%. Pertanto, il nuovo modello di regressione spiega molto meglio il set di dati.

D’altra parte, un’altra indicazione che dobbiamo eseguire la regressione polinomiale è il grafico dei residui. Se in una regressione lineare il grafico dei residui ha la forma di una parabola o di un altro tipo di polinomio, un modello di regressione polinomiale sicuramente si adatta meglio ai dati studiati.

Altri tipi di regressione non lineare

Esistono principalmente tre tipi di regressione non lineare:

Regressione polinomiale – L’equazione del modello di regressione ha la forma di un polinomio.
Regressione logaritmica : viene preso il logaritmo della variabile indipendente.
Regressione esponenziale : la variabile indipendente si trova nell’esponente dell’equazione.

➤ Vedi: Regressione logaritmica
➤ Vedi: Regressione esponenziale

Informazioni sull'autore

Benjamin anderson

Ciao, sono Benjamin, un professore di statistica in pensione diventato insegnante dedicato di Statorials. Con una vasta esperienza e competenza nel campo della statistica, sono ansioso di condividere le mie conoscenze per potenziare gli studenti attraverso Statorials. Scopri di più