Regressione polinomiale in r (passo dopo passo)

La regressione polinomiale è una tecnica che possiamo utilizzare quando la relazione tra una variabile predittore e una variabile di risposta non è lineare.

Questo tipo di regressione assume la forma:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

dove h è il “grado” del polinomio.

Questo tutorial fornisce un esempio passo passo di come eseguire la regressione polinomiale in R.

Passaggio 1: creare i dati

Per questo esempio creeremo un dataset contenente il numero di ore studiate e il voto dell’esame finale per una classe di 50 studenti:

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Passaggio 2: visualizzare i dati

Prima di adattare un modello di regressione ai dati, creiamo innanzitutto un grafico a dispersione per visualizzare la relazione tra le ore studiate e il punteggio dell’esame:

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

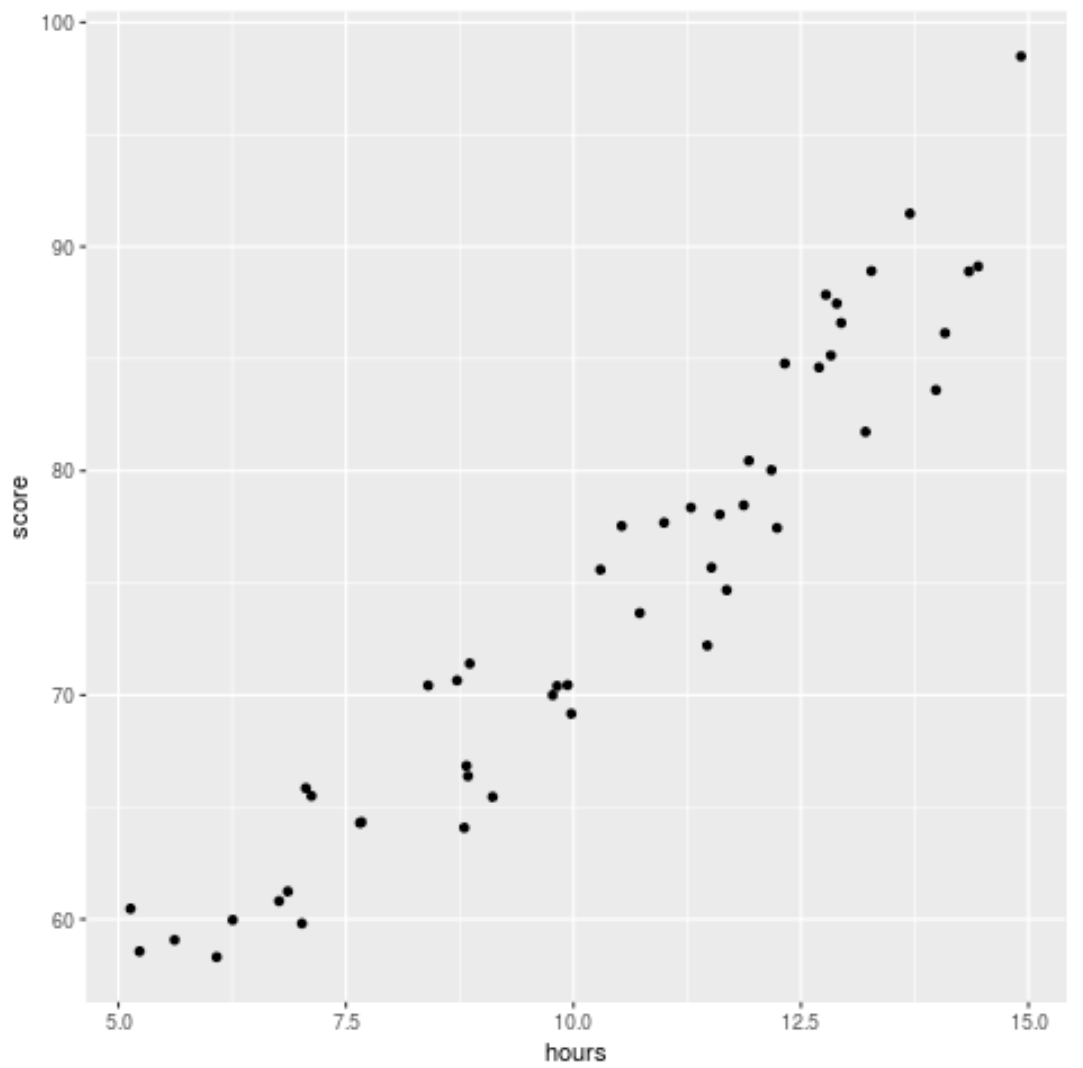
Possiamo vedere che i dati hanno una relazione leggermente quadratica, indicando che la regressione polinomiale potrebbe adattarsi meglio ai dati rispetto alla semplice regressione lineare.

Passaggio 3: adattamento dei modelli di regressione polinomiale

Successivamente, adatteremo cinque diversi modelli di regressione polinomiale con gradi h = 1…5 e utilizzeremo la convalida incrociata k-fold con k = 10 volte per calcolare il test MSE per ciascun modello:

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

Dal risultato possiamo vedere il test MSE per ciascun modello:

• Test MSE con grado h=1: 9,80
• Prova MSE con grado h=2: 8,75
• Prova MSE con grado h=3: 9,60
• Prova MSE con grado h=4: 10,59
• Prova MSE con grado h=5: 13,55

Il modello con il test MSE più basso si è rivelato essere il modello di regressione polinomiale con grado h = 2.

Ciò corrisponde alla nostra intuizione del grafico a dispersione originale: un modello di regressione quadratica si adatta meglio ai dati.

Passaggio 4: analizzare il modello finale

Infine possiamo ricavare i coefficienti del modello più performante:

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Dal risultato, possiamo vedere che il modello finale montato è:

Punteggio = 54,00526 – 0,07904*(ore) + 0,18596*(ore) ²

Possiamo utilizzare questa equazione per stimare il punteggio che uno studente riceverà in base al numero di ore studiate.

Ad esempio, uno studente che studia 10 ore dovrebbe ottenere un voto di 71,81 :

Punteggio = 54,00526 – 0,07904*(10) + 0,18596*(10) ² = 71,81

Possiamo anche tracciare il modello adattato per vedere quanto bene si adatta ai dati grezzi:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

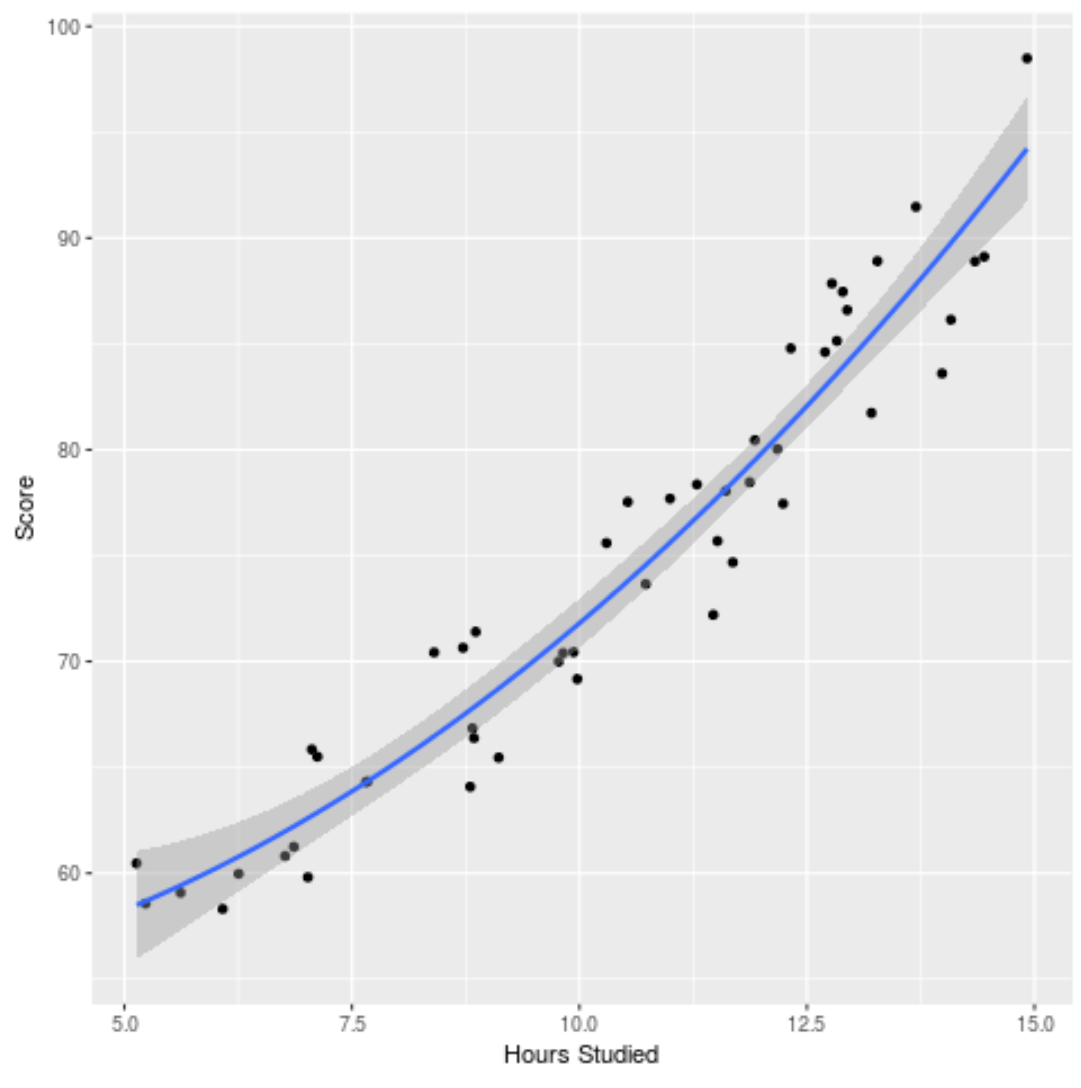
Puoi trovare il codice R completo utilizzato in questo esempio qui .