Come eseguire la regressione quadratica in r

Quando due variabili hanno una relazione lineare, spesso possiamo utilizzare una semplice regressione lineare per quantificare la loro relazione.

Tuttavia, quando due variabili hanno una relazione quadratica, possiamo utilizzare la regressione quadratica per quantificare la loro relazione.

Questo tutorial spiega come eseguire la regressione quadratica in R.

Esempio: regressione quadratica in R

Supponiamo di voler comprendere la relazione tra il numero di ore lavorate e la felicità riportata. Disponiamo dei seguenti dati sul numero di ore lavorate a settimana e sul livello di felicità riportato (su una scala da 0 a 100) per 11 persone diverse:

Utilizzare i seguenti passaggi per adattare un modello di regressione quadratica in R.

Passaggio 1: inserisci i dati.

Per prima cosa creeremo un data frame contenente i nostri dati:

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

Passaggio 2: visualizzare i dati.

Successivamente, creeremo un semplice grafico a dispersione per visualizzare i dati.

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

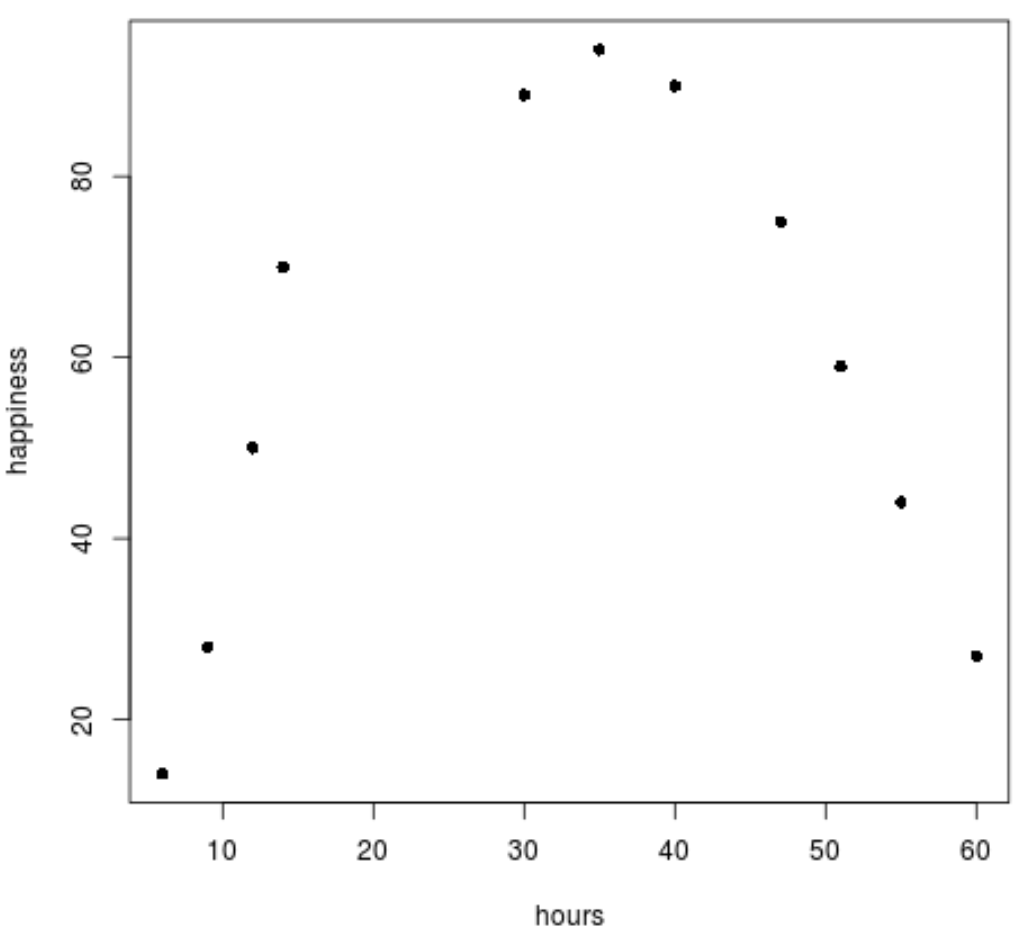
Possiamo vedere chiaramente che i dati non seguono uno schema lineare.

Passaggio 3: adattare un modello di regressione lineare semplice.

Successivamente, adatteremo un semplice modello di regressione lineare per vedere quanto bene si adatta ai dati:

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

La varianza totale della felicità spiegata dal modello è solo del 4,46% , come mostrato dal valore multiplo dell’R quadrato.

Passaggio 4: adattare un modello di regressione quadratica.

Successivamente, adatteremo un modello di regressione quadratica.

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

La varianza totale della felicità spiegata dal modello è aumentata al 96,02% .

Possiamo utilizzare il seguente codice per visualizzare quanto bene il modello si adatta ai dati:

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

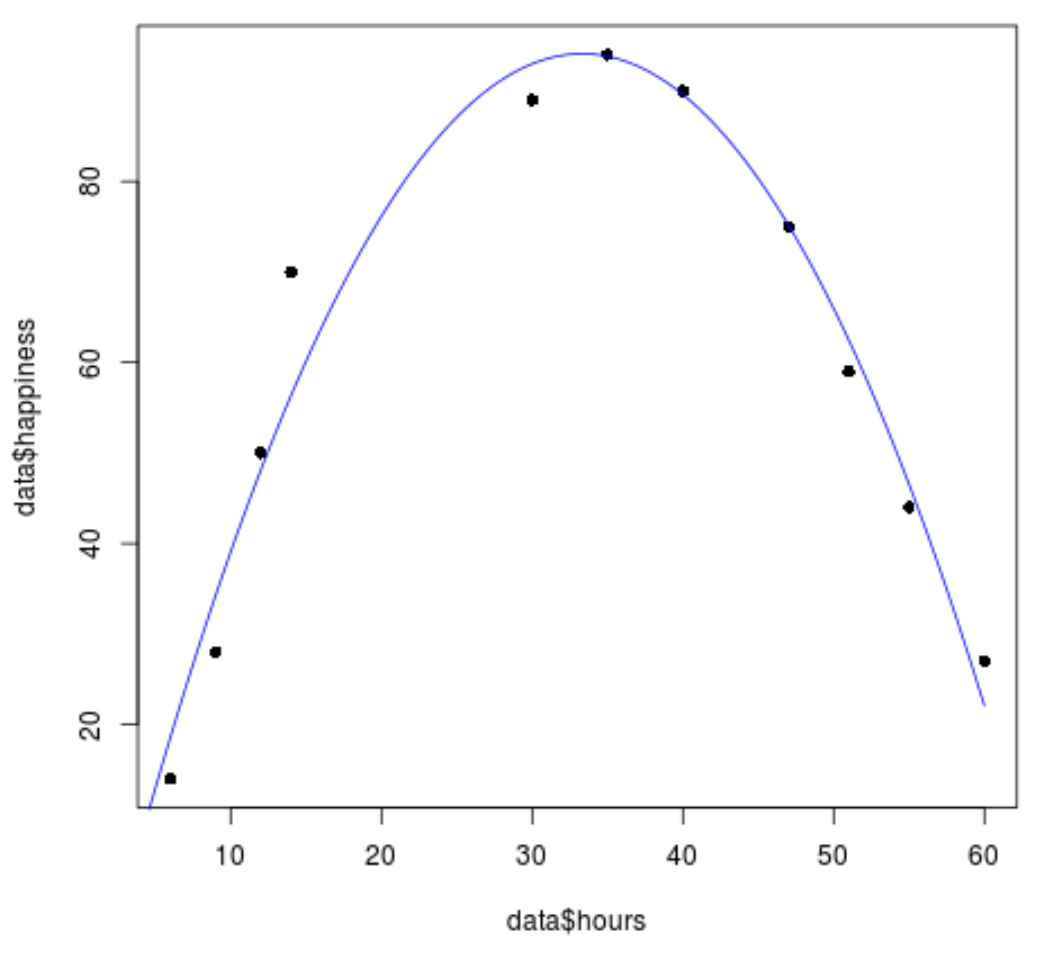
Possiamo vedere che la linea di regressione quadratica si adatta abbastanza bene ai valori dei dati.

Passaggio 5: interpretare il modello di regressione quadratica.

Nel passaggio precedente, abbiamo visto che il risultato del modello di regressione quadratica era:

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

Sulla base dei coefficienti qui presentati, la regressione quadratica corretta sarebbe:

Felicità = -0,1012 (ore) ² + 6,7444 (ore) – 18,2536

Possiamo usare questa equazione per trovare la felicità prevista di un individuo, dato il numero di ore di lavoro settimanali.

Ad esempio, una persona che lavora 60 ore settimanali avrebbe un livello di felicità di 22,09 :

Felicità = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

Al contrario, una persona che lavora 30 ore settimanali dovrebbe avere un livello di felicità di 92,99 :

Felicità = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99