Come eseguire la regressione quantile in python

La regressione lineare è un metodo che possiamo utilizzare per comprendere la relazione tra una o più variabili predittive e una variabile di risposta .

In genere, quando eseguiamo una regressione lineare, vogliamo stimare il valore medio della variabile di risposta.

Tuttavia, potremmo invece utilizzare un metodo noto come regressione quantilica per stimare qualsiasi valore quantile o percentile del valore di risposta, come il 70° percentile, il 90° percentile, il 98° percentile, ecc.

Questo tutorial fornisce un esempio passo passo di come utilizzare questa funzione per eseguire la regressione quantile in Python.

Passaggio 1: caricare i pacchetti necessari

Innanzitutto, caricheremo i pacchetti e le funzioni necessari:

 import numpy as np
import pandas as pd
import statsmodels. api as sm
import statsmodels. formula . api as smf
import matplotlib. pyplot as plt

Passaggio 2: creare i dati

Per questo esempio, creeremo un set di dati contenente le ore studiate e i risultati degli esami ottenuti per 100 studenti di un’università:

 #make this example reproducible
n.p. random . seeds (0)

#create dataset
obs = 100

hours = np. random . uniform (1, 10, obs)
score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100)

df = pd. DataFrame ({' hours ':hours, ' score ':score})

#view first five rows
df. head ()

hours score
0 5.939322 68.764553
1 7.436704 77.888040
2 6.424870 74.196060
3 5.903949 67.726441
4 4.812893 72.849046

Passaggio 3: eseguire la regressione quantilica

Successivamente, adatteremo un modello di regressione quantile utilizzando le ore studiate come variabile predittiva e i punteggi degli esami come variabile di risposta.

Utilizzeremo il modello per prevedere il 90° percentile previsto dei punteggi degli esami in base al numero di ore studiate:

 #fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )

#view model summary
print ( model.summary ())

                         QuantReg Regression Results                          
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
                                        Model: 1
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================

Dal risultato possiamo vedere l’equazione di regressione stimata:

90° percentile del punteggio dell’esame = 59,6104 + 2,8495*(ore)

Ad esempio, il punteggio del 90° percentile di tutti gli studenti che studiano 8 ore dovrebbe essere 82,4:

90° percentile del punteggio dell’esame = 59,6104 + 2,8495*(8) = 82,4 .

L’output visualizza inoltre i limiti di confidenza superiore e inferiore per l’intercetta e i tempi della variabile predittiva.

Passaggio 4: visualizzare i risultati

Possiamo anche visualizzare i risultati della regressione creando un grafico a dispersione con l’equazione di regressione quantilica adattata sovrapposta al grafico:

 #define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])

#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)

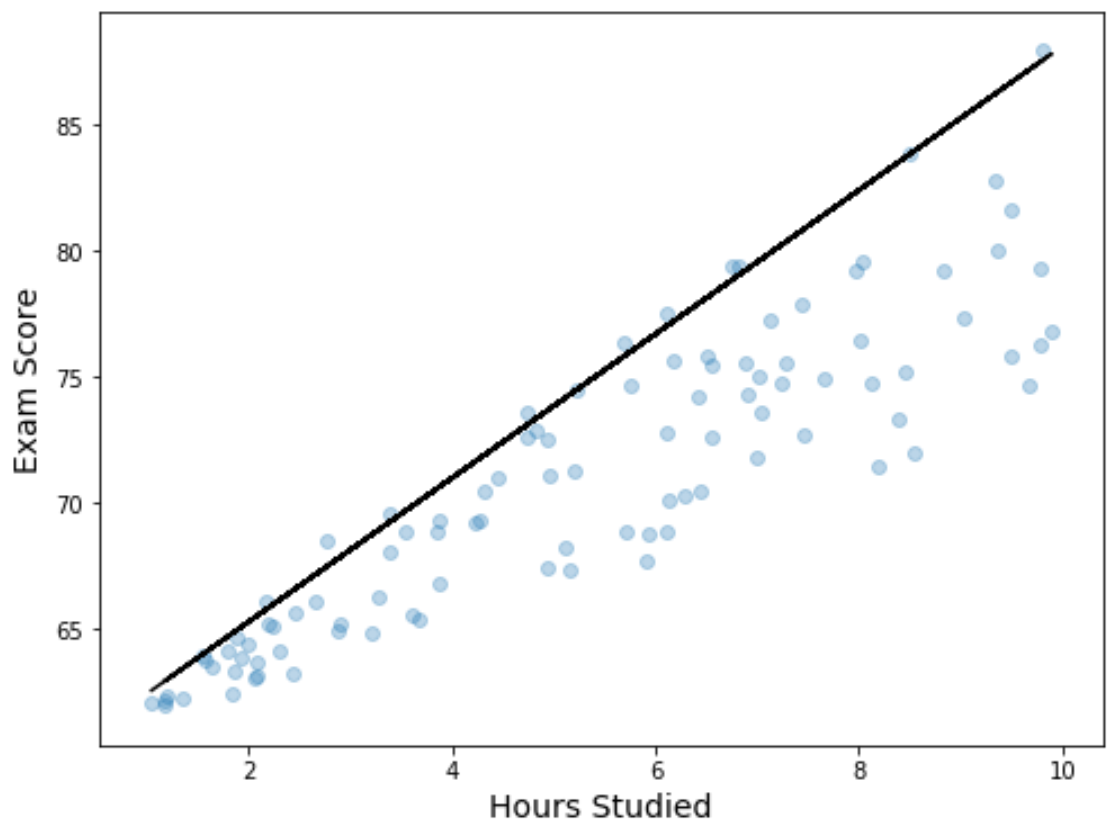
A differenza di una semplice linea di regressione lineare, si noti che questa linea adattata non rappresenta la “linea di migliore adattamento” per i dati. Passa invece attraverso il 90° percentile stimato a ciascun livello della variabile predittrice.

Risorse addizionali

Come eseguire una semplice regressione lineare in Python
Come eseguire la regressione quadratica in Python