Come eseguire la regressione quantile in r

La regressione lineare è un metodo che possiamo utilizzare per comprendere la relazione tra una o più variabili predittive e una variabile di risposta .

In genere, quando eseguiamo una regressione lineare, vogliamo stimare il valore medio della variabile di risposta.

Tuttavia, potremmo invece utilizzare un metodo noto come regressione quantilica per stimare qualsiasi valore quantile o percentile del valore di risposta, come il 70° percentile, il 90° percentile, il 98° percentile, ecc.

Per eseguire la regressione quantile in R, possiamo utilizzare la funzione rq() dal pacchetto quantreg , che utilizza la seguente sintassi:

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

Oro:

• y: la variabile di risposta
• x: la/e variabile/i predittiva/e
• dati: il nome del set di dati
• tau: il percentile da trovare. Il valore predefinito è la mediana (tau = 0,5), ma puoi impostarlo su qualsiasi numero compreso tra 0 e 1.

Questo tutorial fornisce un esempio passo passo di come utilizzare questa funzione per eseguire la regressione quantile in R.

Passaggio 1: inserisci i dati

Per questo esempio, creeremo un set di dati contenente le ore studiate e i risultati degli esami ottenuti per 100 studenti diversi in un’università:

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

Passaggio 2: eseguire la regressione quantilica

Successivamente, adatteremo un modello di regressione quantile utilizzando le ore studiate come variabile predittiva e i punteggi degli esami come variabile di risposta.

Utilizzeremo il modello per prevedere il 90° percentile previsto dei punteggi degli esami in base al numero di ore studiate:

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

Dal risultato possiamo vedere l’equazione di regressione stimata:

Punteggio esame 90° percentile = 60,25 + 2,437*(ore)

Ad esempio, il punteggio del 90° percentile per tutti gli studenti che studiano 8 ore dovrebbe essere 79,75:

90° percentile del punteggio dell’esame = 60,25 + 2,437*(8) = 79,75 .

L’output visualizza inoltre i limiti di confidenza superiore e inferiore per l’intercetta e i tempi della variabile predittiva.

Passaggio 3: visualizzare i risultati

Possiamo anche visualizzare i risultati della regressione creando un grafico a dispersione con l’equazione di regressione quantilica adattata sovrapposta al grafico:

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

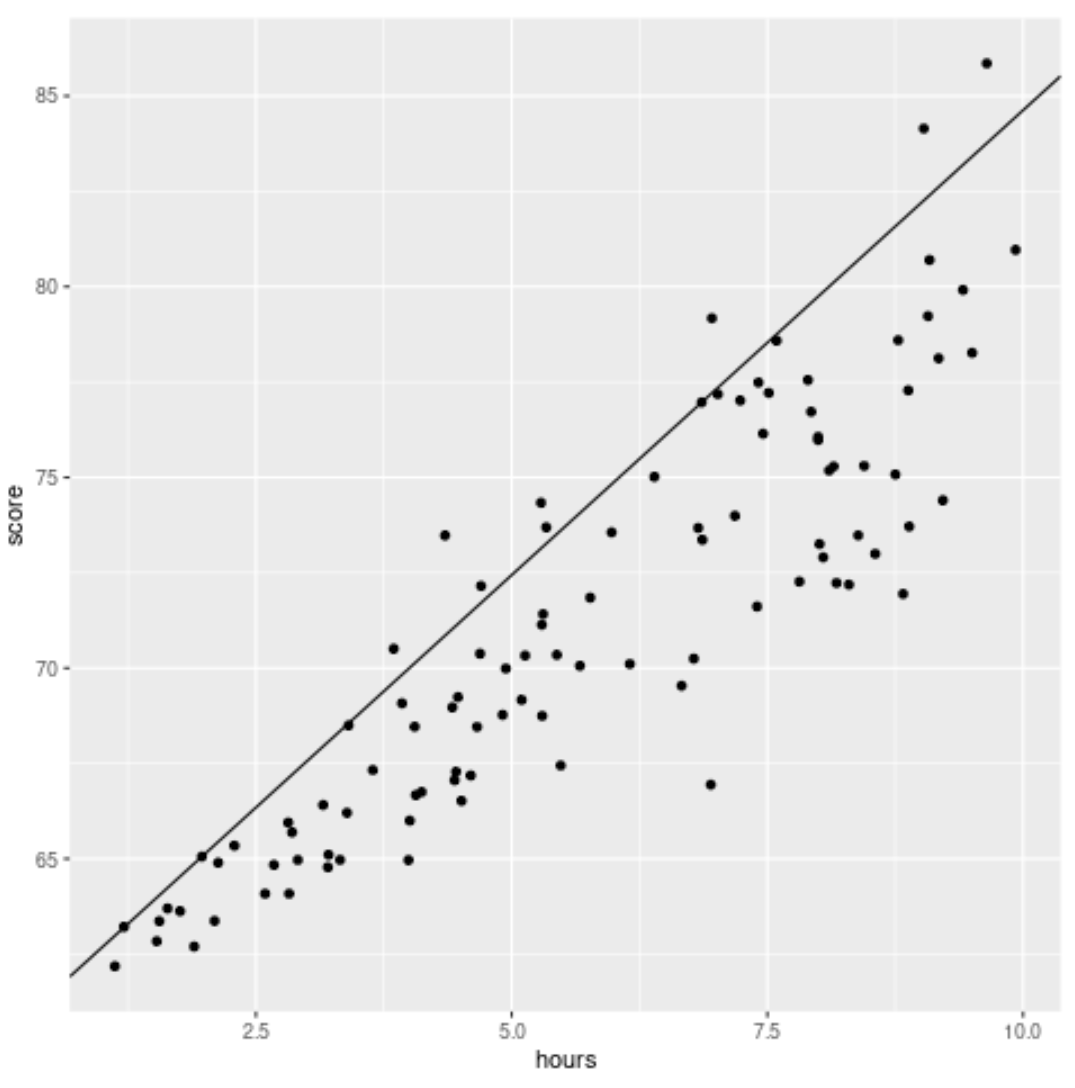
A differenza di una linea di regressione lineare tradizionale, si noti che questa linea adattata non passa attraverso il cuore dei dati. Passa invece attraverso il 90° percentile stimato a ciascun livello della variabile predittrice.

Possiamo vedere la differenza tra l’equazione di regressione quantile adattata e l’equazione di regressione lineare semplice aggiungendo l’argomento geom_smooth() :

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

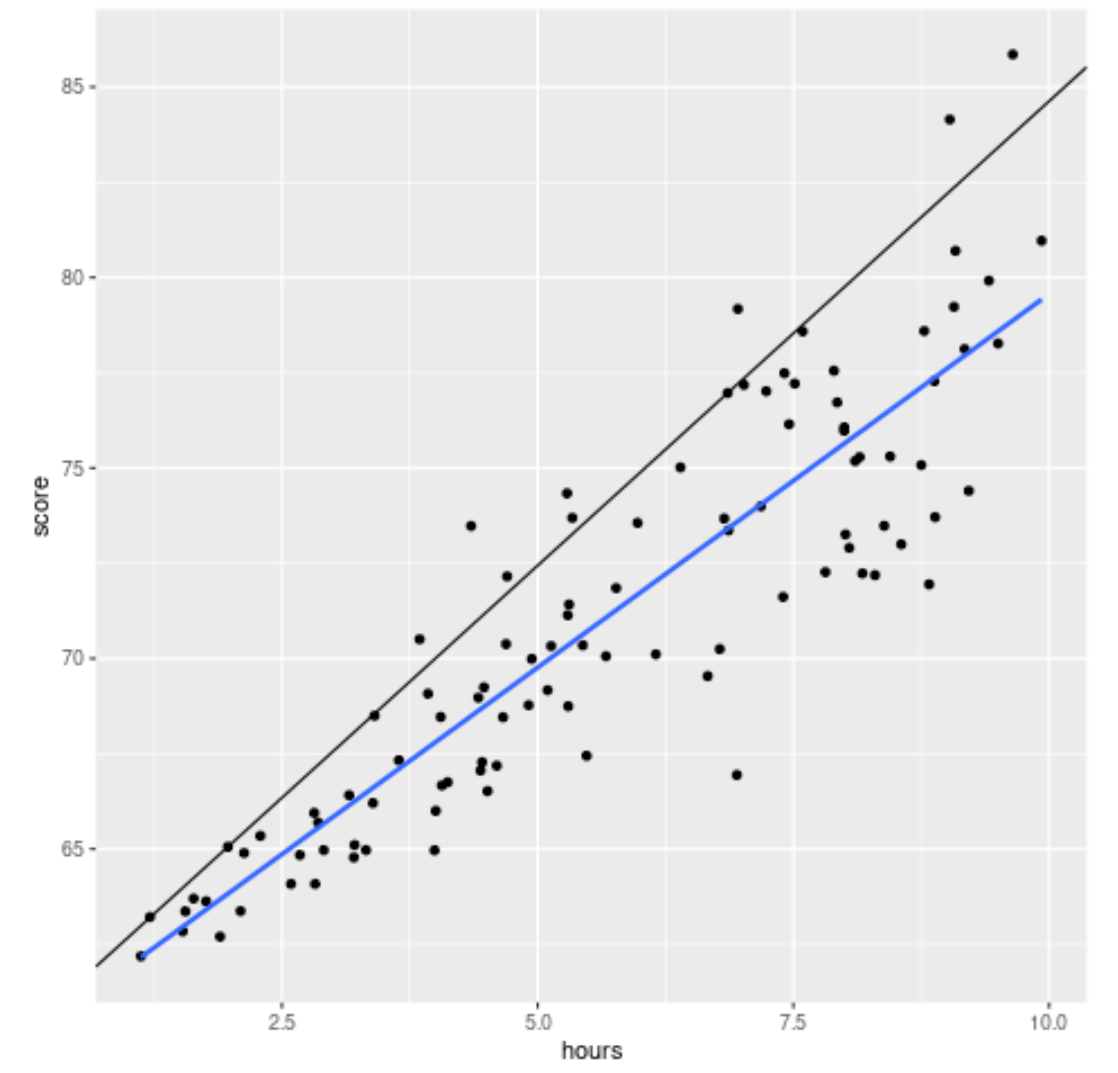
La linea nera mostra la linea di regressione quantile corretta per il 90° percentile e la linea blu mostra la linea di regressione lineare semplice, che stima il valore medio della variabile di risposta.

Come previsto, la retta di regressione lineare semplice attraversa i dati e ci mostra il valore medio stimato dei punteggi degli esami a livello di ogni ora.

Risorse addizionali

I seguenti tutorial spiegano come eseguire altre attività comuni in R:

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come eseguire la regressione quadratica in R