Come eseguire una regressione robusta in r (passo dopo passo)

La regressione robusta è un metodo che possiamo utilizzare come alternativa alla regressione ordinaria dei minimi quadrati quando sono presenti valori anomali o osservazioni influenti nel set di dati con cui stiamo lavorando.

Per eseguire una regressione robusta in R, possiamo utilizzare la funzione rlm() del pacchetto MASS , che utilizza la seguente sintassi:

L’esempio dettagliato seguente mostra come eseguire una regressione robusta in R per un determinato set di dati.

Passaggio 1: creare i dati

Innanzitutto, creiamo un set di dati falso con cui lavorare:

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

Passaggio 2: eseguire la regressione ordinaria dei minimi quadrati

Successivamente, adattiamo un modello di regressione dei minimi quadrati ordinari e creiamo un grafico dei residui standardizzati .

In pratica, spesso consideriamo come un valore anomalo qualsiasi residuo standardizzato il cui valore assoluto sia maggiore di 3.

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

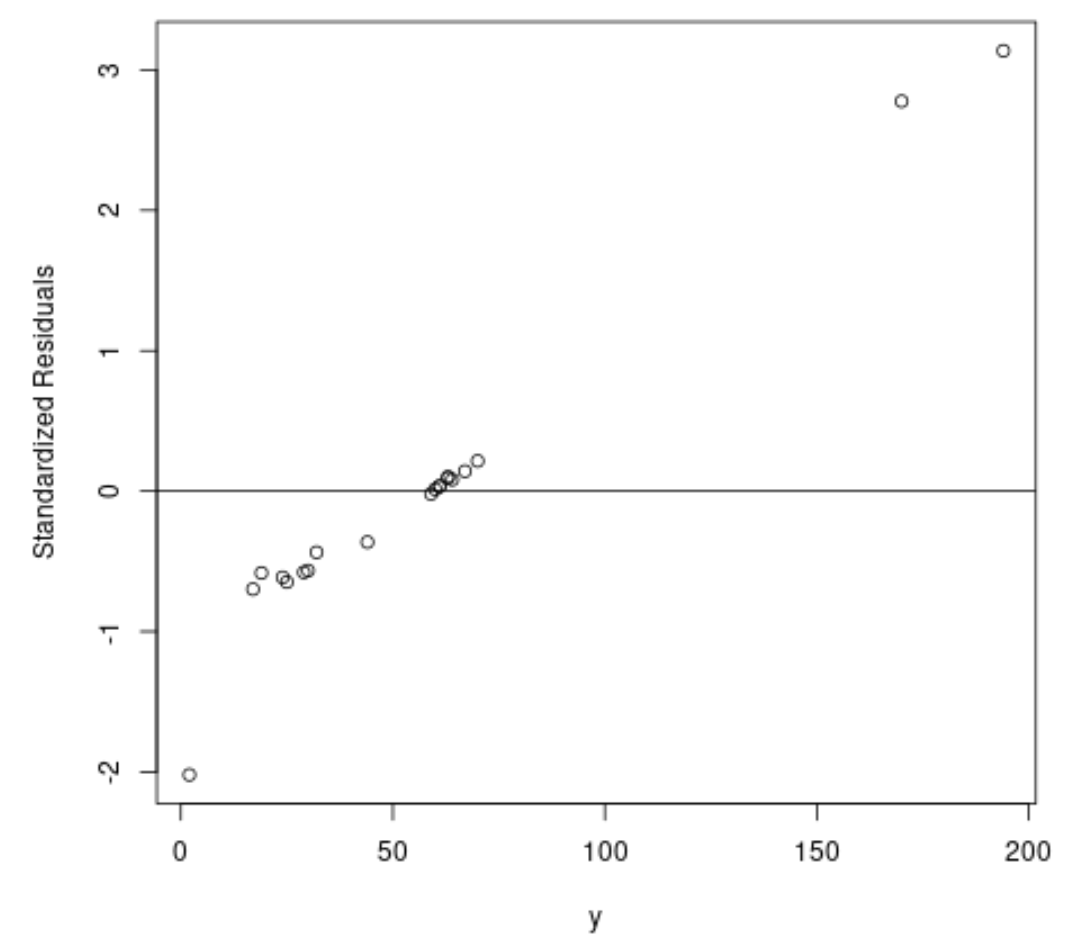
Dal grafico possiamo vedere che ci sono due osservazioni con residui standardizzati intorno a 3.

Ciò indica che ci sono due potenziali valori anomali nel set di dati e quindi potremmo trarre vantaggio da una regressione robusta.

Passaggio 3: eseguire una regressione robusta

Successivamente, utilizziamo la funzione rlm() per adattare un modello di regressione robusto:

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

Per determinare se questo modello di regressione robusto fornisce un adattamento migliore ai dati rispetto al modello OLS, possiamo calcolare l’errore standard residuo di ciascun modello.

L’errore standard residuo (RSE) è un modo per misurare la deviazione standard dei residui in un modello di regressione. Più basso è il valore CSR, migliore è la capacità del modello di adattare i dati.

Il seguente codice mostra come calcolare l’RSE per ciascun modello:

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

Possiamo vedere che l’RSE del modello di regressione robusto è molto inferiore a quello del modello di regressione dei minimi quadrati ordinari, il che ci dice che il modello di regressione robusto fornisce un adattamento migliore ai dati.

Risorse addizionali

Come eseguire una regressione lineare semplice in R
Come eseguire la regressione lineare multipla in R
Come eseguire la regressione polinomiale in R